线性回归,多项式回归(P2)
回归问题
回归问题包含有线性回归和多项式回归
简单来说,线性回归就是用多元一次方程拟合数据,多项式回归是用多元多次来拟合方程
在几何意义上看,线性回归拟合出的是直线,平面。多项式拟合出来的是曲线,曲面。
二,线性回归问题
2.1 线性回归
线性回归问题,是监督学习,输出是连续值。(批梯度下降训练参数+平方误差函数做代价函数)
线性问题的求解另一种方法:正规方程。正规方程把参数看成一个整体进行求导。用矩阵一些性质进行简化结果
正规方程:
思路:用矩阵来表示代价函数,求导数为0的时候参数的值,(最后利用矩阵求导结论,求出参数矩阵。)
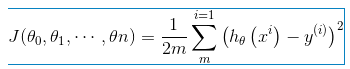
- 用矩阵表示代价函数:
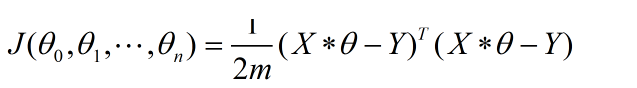 ,
, - 对代价函数求导化简得到正规方程
- 求出Θ。
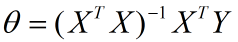
推到过程:
https://blog.csdn.net/melon__/article/details/80589759
https://blog.csdn.net/jshazhang/article/details/78373218
注意:表达式写成矩阵的形式要注意把符号都表示成列向量,还要区分哪些是向量哪些是矩阵,向量和向量的乘积可以互换位置,但是向量和矩阵不行。
注意矩阵相乘写成表达式的样子是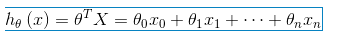 ,但是这是一个样本的矩阵表达,m个样本矩阵的表达形式要写成ΘTX,就要用列向量表示样本向量。即:
,但是这是一个样本的矩阵表达,m个样本矩阵的表达形式要写成ΘTX,就要用列向量表示样本向量。即:
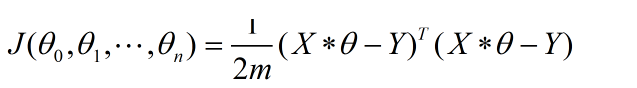 ,其中,写成ΘTX-Y 的形式,或者写成XΘ-Y的形式,这两个表达式里面的X都是样本矩阵,但是是样本矩阵的两种形式,也就是两个X矩阵不一样,前者的X矩阵列向量是一个样本,后者的行向量是一个样本。
,其中,写成ΘTX-Y 的形式,或者写成XΘ-Y的形式,这两个表达式里面的X都是样本矩阵,但是是样本矩阵的两种形式,也就是两个X矩阵不一样,前者的X矩阵列向量是一个样本,后者的行向量是一个样本。
2.2 算法需要注意的地方
数据的归一化(特征缩放):为了保证算法下降得更快。
不管是上神经网络课还是数据挖掘课,老师反复强调了特征的缩放(归一化问题),如果不进行特征的缩放,算法可能就会表现很差,甚至不收敛。特征的缩放方法:Min-Max Scaling和Z-score normalization,
学习率的选取:
通常可以考虑尝试些学习率:0.01,0.03,0.1,0.3,1,3,10
三,多项式回归
对于多项式问题:(多元多次模型)
例如: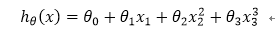

线性回归,多项式回归(P2)的更多相关文章
- 【udacity】机器学习-回归
Evernote Export 1.什么是回归? regression 在监督学习中,包括了输入和输出的样本,在此基础上,我们能够通过新的输入来表示结果,映射到输出 输出包含了离散输出和连续输出 2. ...
- Machine Learning--week2 多元线性回归、梯度下降改进、特征缩放、均值归一化、多项式回归、正规方程与设计矩阵
对于multiple features 的问题(设有n个feature),hypothesis 应该改写成 \[ \mathit{h} _{\theta}(x) = \theta_{0} + \the ...
- 线性回归 Linear Regression
成本函数(cost function)也叫损失函数(loss function),用来定义模型与观测值的误差.模型预测的价格与训练集数据的差异称为残差(residuals)或训练误差(test err ...
- R语言多项式回归
含有x和y这两个变量的线性回归是所有回归分析中最常见的一种:而且,在描述它们关系的时候,也是最有效.最容易假设的一种模型.然而,有些时候,它的实际情况下某些潜在的关系是非常复杂的,不是二元分析所能解决 ...
- stanford coursera 机器学习编程作业 exercise 5(正则化线性回归及偏差和方差)
本文根据水库中蓄水标线(water level) 使用正则化的线性回归模型预 水流量(water flowing out of dam),然后 debug 学习算法 以及 讨论偏差和方差对 该线性回归 ...
- 斯坦福第四课:多变量线性回归(Linear Regression with Multiple Variables)
4.1 多维特征 4.2 多变量梯度下降 4.3 梯度下降法实践 1-特征缩放 4.4 梯度下降法实践 2-学习率 4.5 特征和多项式回归 4.6 正规方程 4.7 正规方程及不可逆性 ...
- Stanford机器学习笔记-1.线性回归
Content: 1. Linear Regression 1.1 Linear Regression with one variable 1.1.1 Gradient descent algorit ...
- 机器学习之多变量线性回归(Linear Regression with multiple variables)
1. Multiple features(多维特征) 在机器学习之单变量线性回归(Linear Regression with One Variable)我们提到过的线性回归中,我们只有一个单一特征量 ...
- (一)线性回归与特征归一化(feature scaling)
线性回归是一种回归分析技术,回归分析本质上就是一个函数估计的问题(函数估计包括参数估计和非参数估计),就是找出因变量和自变量之间的因果关系.回归分析的因变量是应该是连续变量,若因变量为离散变量,则问题 ...
随机推荐
- load balancer does not have available server for client: provider
Ask Question up vote6down votefavorite 4 I'm trying to use Feign client. Below is my feing client: i ...
- java 基础之--传统网络编程
什么是socket ? socket 是连接运行在网络上的两个程序间的双向通讯端点 服务器将某一套接字绑定到一个特定的端口,并通过这一套接字等待和监听客户端的的连接请求 客户端通过这个端口与服务器进行 ...
- MongoDB的增、删、改、查操作(五)
按照我们关系型数据库的思想,一个服务器要想存放数据,首先要有数据库,表,字段,约束,当然了也少不了主键,外键,索引,关系等: 但是在MongoDB的世界里边,我们不用预先的去创建这些信息从而直接来使用 ...
- volley的post请求
//volley发送post请 2 private void volleypost() { 3 String url = "http://apis.juhe.cn/idcard/index? ...
- php 图像处理函数
gd_info 函数:获取当前安装的GD库的信息 getimagesize 函数:获取图像的大小 image_type_to_extension 函数:获取图像类型的文件后缀 ima ...
- VS新建API控制器时提示“运行所选代码生成器时出错”
使用Nuget安装microsoft.entityframeworkcore.tools这个包就行了,安装时注意版本. 根据下图提示应该是新建控制器时用到了这个包,所以安装一下就好了.之前遇到过一次, ...
- C++中find_if
总结:find_if针对查找的对象中包含指针需要进行比较 find则更偏向于普通的数值或者字符比较 两者都可以应用于自定义的类,只需在类中重载==运载符 函数调用符()说白了其实就是代替函数指针,调用 ...
- Android.DebugTools.Traceview & dmtracedump
1. Android 调试工具之Traceview http://www.cnblogs.com/devinzhang/archive/2011/12/18/2291592.html TraceVie ...
- Win7下Qt5的安装及使用
1.安装Qt5 Qt5的安装比Qt4的安装简单多了,我装的是Qt5.4(qt-opensource-windows-x86-mingw491_opengl-5.4.0.exe),它集成了MinGW.Q ...
- RAPID程序设计
1.ABB机器人软件 RobotWare 是ABB提供的机器人系列应用软件的总称. RobotStudio是ABB公司自行开发的机器人模拟软件, 能在PC机上模拟几乎所有型号的ABB 机器人几乎所有的 ...
