Ng第四课：多变量线性回归(Linear Regression with Multiple Variables)

4.1 多维特征

4.2 多变量梯度下降

4.3 梯度下降法实践 1-特征缩放

4.4 梯度下降法实践 2-学习率

4.5 特征和多项式回归

4.6 正规方程

4.7 正规方程及不可逆性（可选）

4.1 多维特征

目前为止，探讨了单变量/特征的回归模型，现在对房价模型增加更多的特征

增添更多特征后，引入一系列新的注释：

n 代表特征的数量

支持多变量的假设 h 表示为

这个公式中有 n+1 个参数和 n个变量，为了使得公式能够简化一些，引入 x0=1，则公式转化为：

此时模型中的参数是一个 n+1 维的向量，任何一个训练实例也都是 n+1 维的向量，特征矩阵 X 的维度是 m*(n+1)。

推理图如下： #大红框表示满足了矩阵乘法条件

4.2 多变量梯度下降

与单变量线性回归类似，在多变量线性回归中，也构建一个代价函数，则这个代价函数是所有建模误差的平方和，即：

其中

我们的目标和单变量线性回归问题中一样，是要找出使得代价函数最小的一系列参数。

多变量线性回归的批量梯度下降算法为： #与单变量仅在J()中不同

因为J(θ₀,θ1,...,θn) = ，即：

求导数后得到： #在J(θ₀,θ1,...,θn)中对θ_j求偏导

单/多变量梯度下降算法比较如图： #仅末尾的

不同，

4.3 梯度下降法实践1-特征缩放

在面对多维特征问题的时候，要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛。

以房价问题为例，假设使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0-2000 平方英尺，而房间数量的值则是 0-5，以两个参数分别为横纵坐标，绘制代价函数的等高线图能，看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

第一种解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。如图：

第二种通用方法是令：

4.4 梯度下降法实践2-学习率

梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，不能提前预知，但是可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。也有一些自动测试是否收敛的方法，例如将代价函数的变化值与某个阀值（例如 0.001）进行比较，但通常看上面这样的图表更好。

梯度下降算法的每次迭代受到学习率的影响，如果学习率 α 过小，则达到收敛所需的迭代次数会非常高；如果学习率 α 过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。通常可以考虑尝试些学习率：α=0.01，0.03，0.1，0.3，1，3，10

4.5 特征和多项式回归

如房价预测问题，

X₁=frontage（临街宽度），x₂=depth（纵向深度），x=frontage*depth=area（面积），则 hΘ（x）=Θ₀+Θ₁x

有时候线性回归并不适用于所有数据，需要曲线来适应我们的数据，

比如一个二次方模型：

或者三次方模型：

通常我们需要先观察数据然后再决定准备尝试怎样的模型。另外，我们可以令：

从而将模型转化为线性回归模型，这也是特征缩放的一种。

根据函数图形特性，我们还可以使：

或者：

注：如果采用多项式回归模型，在运行梯度下降算法前，特征缩放非常有必要。

4.6 正规方程

到目前为止，我们都在使用梯度下降算法，但是对于某些线性回归问题，正规方程方法是更好的解决方案。如：

正规方程是通过求解下面的方程来找出使得代价函数最小的参数的：

假设我们的训练集特征矩阵为 X（包含了 x0=1）并且我们的训练集结果为向量 y，则利用正规方程解出向量

设矩阵

以下表示数据为例：

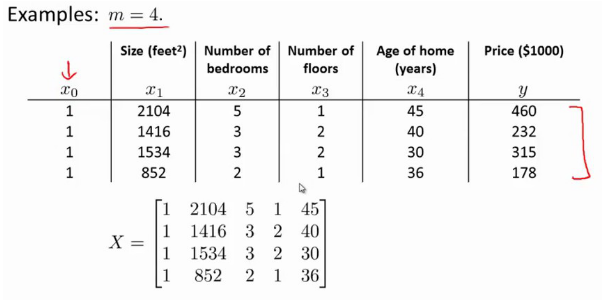
即：

运用正规方程方法求解参数：

在 Octave 中，正规方程写作：

pinv(X'*X)*X'*y

注：对于那些不可逆的矩阵（通常是因为特征之间不独立，如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征，也有可能是特征数量大于训练集的数量，比如有2000个特征但是只有1000个训练集），正规方程方法是不能用的。

梯度下降与正规方程的比较：

总结一下，只要特征变量的数目并不大，标准方程是一个很好的计算参数θ的替代方法。具体地说，只要特征变量数量小于一万，我通常使用正规方程法，而不使用梯度下降法。随着我们要讲的学习算法越来越复杂，例如，当我们讲到分类算法，像逻辑回归算法，我们会看到，实际上对于那些算法，并不能使用标准方程法。对于那些更复杂的学习算法，我们将不得不仍然使用梯度下降法。因此，梯度下降法是一个非常有用的算法，可以用在有大量特征变量的线性回归问题。或者我们以后在课程中，会讲到的一些其他的算法，因为正规方程法不适合或者不能用在它们上。但对于这个特定的线性回归模型，最后正规方程法是一个比梯度下降法更快的替代算法。所以，根据具体的问题，以及你的特征变量的数量，这两种算法都是值得学习的。