GM11灰色模型
作者:桂。
时间:2017-08-12 08:34:06
链接:http://www.cnblogs.com/xingshansi/p/7348714.html
前言
灰色模型(Gray model)常用来对数据进行预测,这里简要记录其思路。
一、名称由来
常见系统分类:
- 白色系统是指一个系统的内部特征是完全 已知的,即系统的信息是完全充分的。
- 黑色系统是指一个系统的内部信息对外界来说是一无所知的,只能通过它与外界的联系来加以观测研究。
- 灰色系统内的一部分信息是已知的,另一部分信息是未知的,系统内各因素间有不确定的关系。
二、算法原理

.png)

.png)
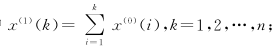
.png) 假设生成序列的一阶模型(核心思想):
假设生成序列的一阶模型(核心思想):
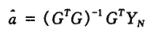
.png)
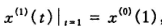
将其带入上面一阶方程解(参数已求出)
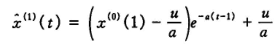 取t为离散值(t = k+1)
取t为离散值(t = k+1)
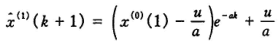 而
而
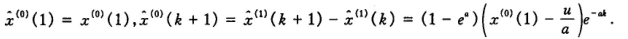
这样便完成了预测。
.png)
主函数
clc;clear all;close all
set(0,'defaultfigurecolor','w');
%{
参考:《离散模型与灰色预测模型建模机理》,谢乃明,刘思峰
本程序主要用来计算根据灰色理论建立的模型的预测值。
应用的数学模型是 GM(1,1)。
原始数据的处理方法是一次累加法。
%}
f = @(t,b)(0.3*t.^2+b+0.3*randn(1,length(t)));%定义待预测函数
t = 0:.2:5;
b = 3;
x0 = f(t,b);
x_pre = GM11(x0);
plot(t,x0,'k',t,x_pre,'r--');
xlabel('时间(年)');
ylabel('幅度');
title('GM11预测模型');
legend('原始数据','预测数据');
GM11的function:
function x_pre = GM11(x0)
x0 = x0(:);
n = length(x0);
x1 = cumsum(x0);
for i = 1:n-1
G(i,1) = -(x1(i)+x1(i+1))/2;
G(i,2) = 1;
end
Y = x0(2:end);
belta = pinv(G'*G)*G'*Y;
a = belta(1);
u = belta(2);
%predict
x_pre1 = zeros(n,1);
x_pre = x_pre1;
for k = 0:n-1
x_pre1(k+1) = (x0(1)-u/a)*exp(-a*k)+u/a;
end
x_pre(1) = x0(1);
for k = 1:n-1
x_pre(k+1) = x_pre1(k+1)-x_pre1(k);
end
结果图:
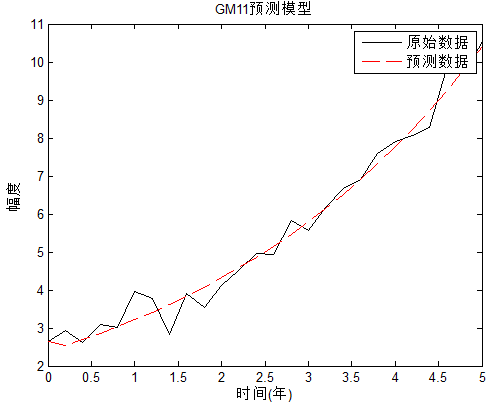
GM11灰色模型的更多相关文章
- python 实现 灰色预测 GM(1,1)模型 灰色系统 预测 灰色预测公式推导
来源公式推导连接 https://blog.csdn.net/qq_36387683/article/details/88554434 关键词:灰色预测 python 实现 灰色预测 GM(1,1)模 ...
- R实现灰色预测
1.简介 预测就是借助于对过去的探讨去推测.了解未来.灰色预测通过原始数据的处理和灰色模型的建立,发现.掌握系统发展规律,对系统的未来状态做出科学的定量预测.对于一个具体的问题,究竟选择什么样的预测模 ...
- 【数学建模】灰色系统理论II-Verhulst建模-GM(1,N)-GM(2,1)建模
灰色系统理论中,GM(1,1)建模很常用,但他是有一定适应范围的. GM(1,1)适合于指数规律较强的序列,只能描述单调变化过程.对于具有一定随机波动性的序列,我们考虑使用Verhulst预测模型,或 ...
- NLP&数据挖掘基础知识
Basis(基础): SSE(Sum of Squared Error, 平方误差和) SAE(Sum of Absolute Error, 绝对误差和) SRE(Sum of Relative Er ...
- 3Dmax+blend+WPF综合运用
原文:3Dmax+blend+WPF综合运用 赛后总结 本人小菜,WPF刚入门,只是写一下最近的项目心得.欢迎各位前辈们前来拍砖指正,感激不敬!先申明,小弟我入门仓促,很多东西也是一知半解,所以很多问 ...
- 常见的机器学习&数据挖掘知识点
原文:http://blog.csdn.net/heyongluoyao8/article/details/47840255 常见的机器学习&数据挖掘知识点 转载请说明出处 Basis(基础) ...
- 2019第九届MathorCup数学建模
题目下载:https://www.lanzous.com/i3taz2j 总共四个问题 问题1 首先附件一中的数据,拿到后肯定感觉棘手.我们的处理方法: 在下面缺失数据的地方我们都认为是问题3中的预测 ...
- WPF--3Dmax+blend+WPF综合运用
引自:http://blog.sina.com.cn/s/blog_95dbdf9e0100we3z.html 本人小菜,WPF刚入门,只是写一下最近的项目心得.欢迎各位前辈们前来拍砖指正,感激不敬! ...
- Unreal Engine 4 系列教程 Part 6:动画教程
.katex { display: block; text-align: center; white-space: nowrap; } .katex-display > .katex > ...
随机推荐
- 关于block的回调使用-防止内存泄露问题
block 一般用于回调,比方请求数据我们把asi封装好,仅仅用block调数据就方便很多 获取到得数据假设要给之加入数据,切记不能够使用self.(这个数组) 或者_(这个数组) addObject ...
- 将War发布到Tomcat7上遇到的问题及其解决
用MyEclipse做了一个app,在其自带的Tomcat里运行正常,做成war后却出现如下错误: [ServletException in:/page/jsp/template/block.jsp] ...
- Tomcat之安装篇- 1
1. 提供了下载页面 以及tomcat下载地址,点击即可下载 : Tomcat9.0(Windows64) 方便好用的录像机下载请点击: gif工具 即可下载. 2.下载好的压缩包进行解压 3.配置路 ...
- MySQL优化小案例:key_buffer_size
key_buffer_size是对MyISAM表性能影响最大的一个参数,下面一台以MyISAM为主要存储引擎服务器的配置: mysql> SHOW VARIABLES LIKE '%key_bu ...
- rxvt-unicode配置
我的urxvt配置文件如下 前缀可改为rxvt然后可以使用rxvt命令启动 -/.Xresources ! urxvt color set URxvt.multichar_encoding:utf-8 ...
- ORA-22828 输入样式或替换參数超过了32k限制大小
今天调试程序报下面错误: ORA-22828: input pattern or replacement parameters exceed 32K size limit 22828. 00000 - ...
- HTTP协议详解之URL篇
•HTTP URL基本格式: <http://host[:port][abs_path] / [;parameters][?query]#fragment> 1)http:表示要通过HTT ...
- 新浪微博API使用初步介绍——解决回调地址的问题
# -*- coding: utf-8 -*- #python 27 #xiaodeng #新浪微博API使用初步介绍——解决回调地址的问题 #http://blog.csdn.net/monsion ...
- Tomcat跨二级域配置
内容转自:http://blog.csdn.net/luka2008/article/details/38385703/,请直接看原文,不过这篇“原文”也是转的... 1,Tomcat下 代码: im ...
- 用户研究Q&A(1)
近来,不少同事开始认同用户研究的价值,希望通过接触,理解和研究用户来获取提升产品的有效信息.这绝对是件好事,因为我一直抱持的理念是,研究并不是藏在实验室或者握在少部分人手中的稀罕货,更重要是一种理念和 ...

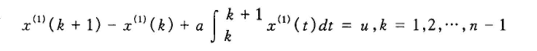
.png)

.png)
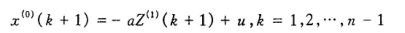
.png)
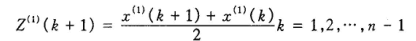
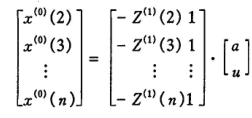
.png)
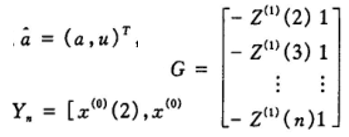 计算均值生成序列:
计算均值生成序列:.png)