【BZOJ 2820】 YY的GCD （莫比乌斯+分块）

YY的GCD

 

Description

神犇YY虐完数论后给傻×kAc出了一题

给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对

kAc这种傻×必然不会了，于是向你来请教……

多组输入

Input

第一行一个整数T 表述数据组数

接下来T行，每行两个正整数，表示N, M

Output

T行，每行一个整数表示第i组数据的结果

Sample Input

2
10 10
100 100

Sample Output

30
2791

Hint

T = 10000

N, M <= 10000000

【分析】

　　

　　当Prime确定时，跟bzoj1101一样，得 ：
　　...=∑u[d]*(n/(Pri*d))*(m/(pri*d))     但是暴力枚举Pri应该很慢吧~~多组诶~~

　　然后通过前面几题我们知道u这里是可以快速求和的，而我们尽量让(n/(Pri*d))*(m/(pri*d) 这个部分是确定的，那么搞完u之后就可以直接√n分块了。

　　所以不妨设k=pri*d，把k变成我们要枚举的东西，原式= ∑u[k/Pri]*(n/k)*(m/k)  。

　　问题就变成求u[k/Pri]，它的意义是什么呢？相当于     - >

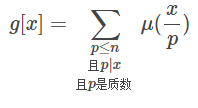这个东西~~

　　这个东西表示蒟蒻的脑子是想不出来怎么求的~~

　　直接放大神的解析：~~

　　

　　好像很有道理哦！！！！！

　　除了熟悉的积性函数，其他的我都不会线性筛了~~真是太年轻！！！

　　然后可爱的分块就可以了。

代码如下：

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 #include<cmath>
 using namespace std;
 #define Maxn 10000010
 #define LL long long

 LL mu[Maxn],pri[Maxn],h[Maxn],g[Maxn],pl;
 bool q[Maxn];

 LL mymin(LL x,LL y) {return x<y?x:y;}

 void get_mu(LL mx)
 {
     pl=;
     memset(q,,sizeof(q));
     mu[]=;g[]=;
     for(LL i=;i<=mx;i++)
     {
         if(q[i])
         {
             pri[++pl]=i;
             mu[i]=-;g[i]=;
         }
         for(LL j=;j<=pl;j++)
         {
             if(i*pri[j]>mx) break;
             q[i*pri[j]]=;
             if(i%pri[j]==) mu[i*pri[j]]=,g[i*pri[j]]=mu[i];
             else mu[i*pri[j]]=-mu[i],g[i*pri[j]]=mu[i]-g[i];
             if(i%pri[j]==) break;
         }
     }
     h[]=g[];
     for(int i=;i<=mx;i++) h[i]=h[i-]+g[i];
 }

 int main()
 {
     freopen("a.in","r",stdin);
     freopen("a.out","w",stdout);
     get_mu();
     int T;
     scanf("%d",&T);
     while(T--)
     {
         LL n,m,t;
         scanf("%lld%lld",&n,&m);
         if(n>m) t=n,n=m,m=t;

         LL ans=;

         LL sq=(LL)ceil(sqrt((double)m));
         for(LL i=;i<=mymin(sq,n);i++)
         {
             ans+=g[i]*(n/i)*(m/i);
         }

         for(LL i=sq+;i<=n;)
         {
             LL x=n/i,y=m/i;
             LL r1=n/x+,r2=m/y+;
             LL r=mymin(r1,r2);
             if(r>m+) r=m+;
             ans+=(h[r-]-h[i-])*x*y;
             i=r;
         }

         printf("%lld\n",ans);

     }
     return ;
 }

[BZOJ2820]

2016-08-30 11:45:40