机器学习基石笔记:06 Theory of Generalization








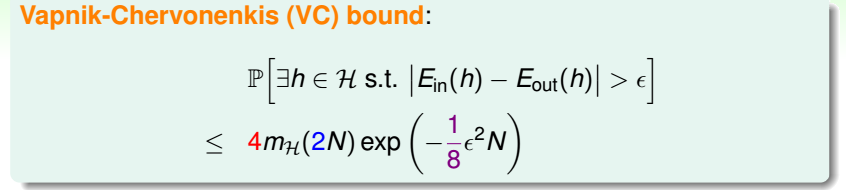
机器学习基石笔记:06 Theory of Generalization的更多相关文章
- 机器学习基石:06 Theory of Generalization
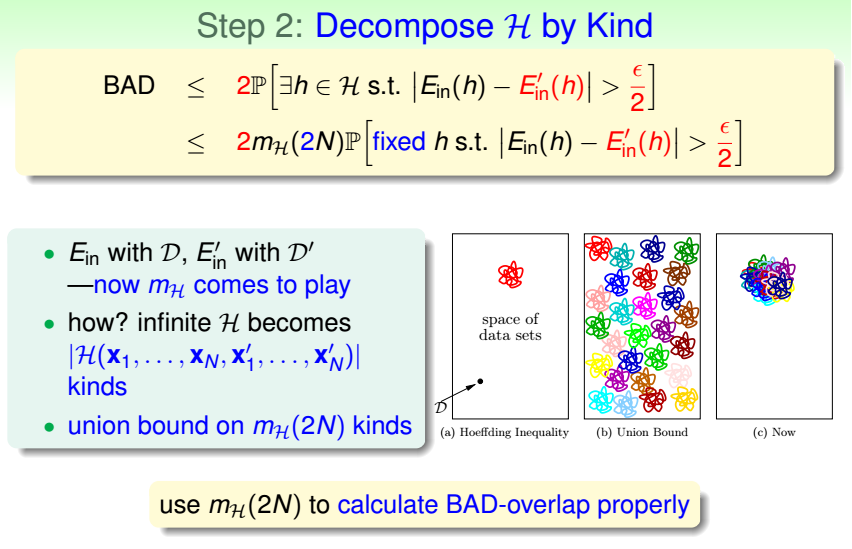
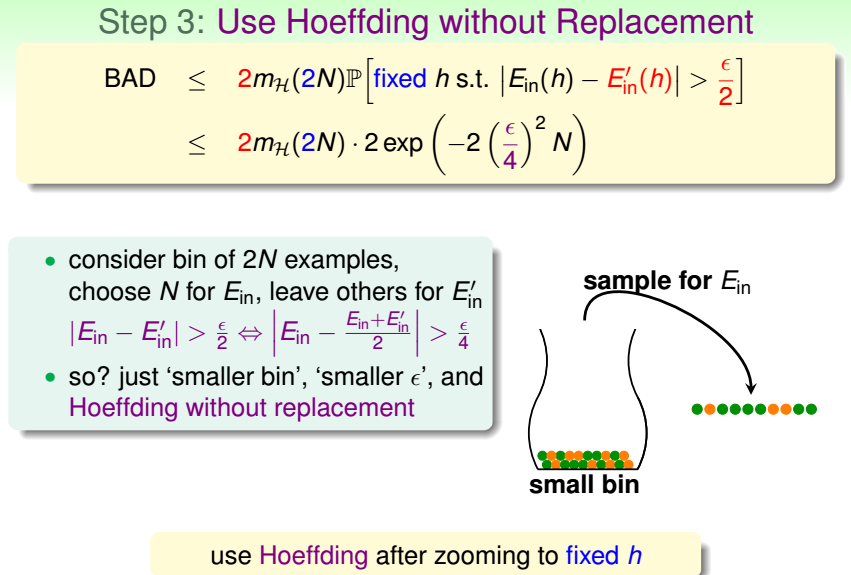
若H的断点为k,即k个数据点不能被H给shatter,那么k+1个数据点也不能被H给shatter,即k+1也是H的断点. 如果给定的样本数N是大于等于k的,易得mH(N)<2N,且随着N的增大 ...
- Coursera台大机器学习课程笔记5 -- Theory of Generalization
本章思路: 根据之前的总结,如果M很大,那么无论假设泛化能力差的概率多小,都无法忽略,所以问题转化为证明M不大,然后上章将其转化为证明成长函数:mh(N)为多项式级别.直接证明似乎很困难,本章继续利用 ...
- 机器学习基石笔记:01 The Learning Problem
原文地址:https://www.jianshu.com/p/bd7cb6c78e5e 什么时候适合用机器学习算法? 存在某种规则/模式,能够使性能提升,比如准确率: 这种规则难以程序化定义,人难以给 ...
- 机器学习基石笔记:04 Feasibility of Learning
原文地址:https://www.jianshu.com/p/f2f4d509060e 机器学习是设计算法\(A\),在假设集合\(H\)里,根据给定数据集\(D\),选出与实际模式\(f\)最为相近 ...
- 林轩田机器学习基石笔记4—Feasibility of Learning
上节课介绍了机器学习可以分为不同的类型.其中,监督式学习中的二元分类和回归分析是最常见的也是最重要的机器学习问题.本节课,我们将介绍机器学习的可行性,讨论问题是否可以使用机器学习来解决. 一.Lear ...
- 林轩田机器学习基石笔记3—Types of Learning
上节课我们主要介绍了解决线性分类问题的一个简单的方法:PLA.PLA能够在平面中选择一条直线将样本数据完全正确分类.而对于线性不可分的情况,可以使用Pocket Algorithm来处理.本节课将主要 ...
- 林轩田机器学习基石笔记2—Learning to Answer Yes/No
机器学习的整个过程:根据模型H,使用演算法A,在训练样本D上进行训练,得到最好的h,其对应的g就是我们最后需要的机器学习的模型函数,一般g接近于目标函数f.本节课将继续深入探讨机器学习问题,介绍感知机 ...
- 林轩田机器学习基石笔记1—The Learning Problem
机器学习分为四步: When Can Machine Learn? Why Can Machine Learn? How Can Machine Learn? How Can Machine Lear ...
- 06 Theory of Generalization
若H的断点为k,即k个数据点不能被H给shatter,那么k+1个数据点也不能被H给shatter,即k+1也是H的断点. 如果给定的样本数N是大于等于k的,易得mH(N)<2N,且随着N的增大 ...
随机推荐
- ubuntu开启远程shell,开启上传下载
需要先安装openshell-server 具体命令如下: 1.先更新下源 sudo apt-get update 2.安装openshell-server sudo apt-get install ...
- TaskScheduler
一初始化 在SparkContext初始化的时候,同时初始化三个对象.DAGScheduler,TaskScheduler,SchedulerBackend.DAGScheduler,前面已经讲到,做 ...
- springboot整合dubbox与zookeeper
springboot中dubbo依赖的引入和配置(application.properties)参见:https://blog.csdn.net/wohaqiyi/article/details/72 ...
- CentOS7 安装oracle客户端
1.本机环境CentOS7 64 [root@localhost etc]# uname -a Linux localhost.localdomain 3.10.0-693.el7.x86_64 #1 ...
- php一些简单的作业题
- [SoapUI] 从测试套件,测试用例,测试步骤,测试数据各个级别控制是否执行
自动保存 # -*- coding: utf-8 -*- import java.awt.Color import org.apache.poi.ss.usermodel.Cell import or ...
- 图解HTTP第一章
了解 Web 及网络基础 Web 页面是如何呈现的吗? Web 使用一种名为 HTTP(HyperText Transfer Protocol,超文本传输协议)的协议作为规范,完成从客户端到服务器端等 ...
- C++ MFC棋牌类小游戏day3
今天开始设计小人棋子. 画法跟画虎一样,唯一不一样的是小人在刚开始会有重叠的情况,所以画起来可能比虎的棋子能够难一点. 我打算用Location结构体中的num来标记每个棋盘坐标存在棋子的个数,isH ...
- PCL-Kinfu编译手册
1:配置要求 硬件 Win7-62bit 显卡需要compute Capability >=2.0 可以从https://developer.nvidia.com/cuda-gpus 中查找 实 ...
- 06-jQuery的文档操作
之前js中咱们学习了js的DOM操作,也就是所谓的增删改查DOM操作.通过js的DOM的操作,大家也能发现,大量的繁琐代码实现我们想要的效果.那么jQuery的文档操作的API提供了便利的方法供我们操 ...
