斜率DP个人理解

斜率DP

斜率DP的一版模式：给你一个序列，至多或分成m段，每段有花费和限制，问符合情况的最小花费是多少；

一版都用到sum[]，所以符合单调，然后就可以用斜率优化了，很模板的东西；

如果看不懂可以先去看一下本博客----斜率DP题目，看一下第一道题目，然后在回来看push,pop是为什么这样操作；

首先通过对方程的化简得到如下递推方程
DP[i] = min/max( -a[i]*x[j] + y[j] ) + w[i]; (1<=j<i)

一般情况下，x[j],y[j]，a[i]都是单调递增的，(求最小值,维护的是下右凸包)
当然也可以x[j]单调递减，y[j]单调递增，a[i]单调递增；(求最小值，维护的是下左凸包)

对于DP[i],显然只要找到一个j使a[i]*x[j]+y[j]最小就可以了，
注意对于DP[i]来说，a[i],w[i]都是常量;

一般对于DP[i] =min/max(-a[i]*x[j] + y[j] )+ w[i],最朴素的时间复杂度是O(n^2);
为什么可以优化呢

设G = -a[i]*x[j] + y[j],
移项： y[j] = a[i]*x[j] + G;
现在的问题就是：已知道a[i]也就是斜率，给你几个点（x[j],y[j]），找一个点带入使得G最小；
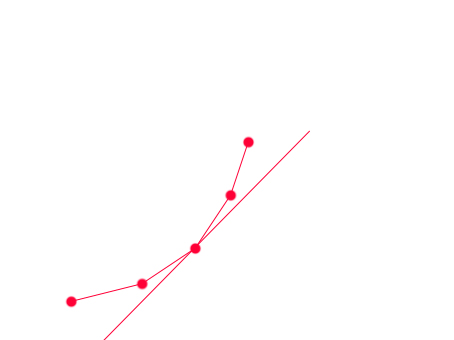
G是直线与Y轴的交点的纵坐标的值，显然这个点一定在这些点形成的凸包上，

（图是x[i],y[i],单调递增，斜率为正的情况）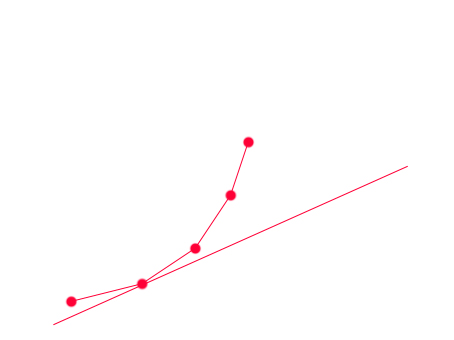

因为我们在从小到大递推求解，求DP[i]的时候DP[j]（0<=j<i）都是已知的
所以我们可以在求完DP[i]之后可以马上把点（x[i],y[i]）加入，来维护一个凸包；

这里还需要一个小知识点，就是凸包的维护，如果写过凸包的话，我们都知道在维护前
都要先把点排序（不管是水平序，还是极角序）
这就是为什么要x[i],y[i]是单调的原因了，只有单调才可以按照递推的顺序直接维护凸包了；

但如果所有的点都在凸包上，那么这个优化也就不算优化了，

所以问题变成：
对于一条已知斜率的直线，如何从凸包上找一个点使它与Y轴的交点的纵坐标值最小；

对于一个下凸包，且斜率单调递增：（求最小值的情况下）
我们现在假设直线和下凸包里斜率最小的直线重合，不断的变大这条直线的斜率，
也就是沿着这个凸包旋转，
我们发现，这条直线要么跟凸包的一条直线重合，要么经过凸包的一个点，
且一旦一个点被旋转过去后，接下来斜率变大的直线都不可会再经过这个点重合，
也就是说一旦一个点被淘汰了，那么它在接下来的过程中也不会被用到，

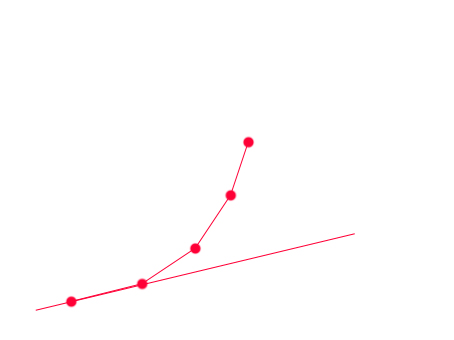
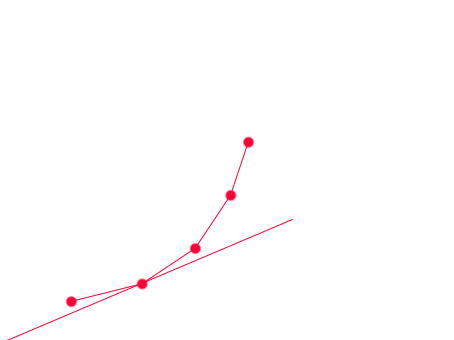
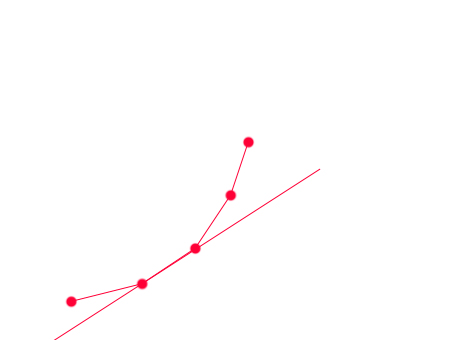
这样我们就有一个O(n)的算法，每次从凸包队列里从头比较相临的俩个点，谁得到的G
比较小，如果后一个点得到的G小，说明前一个点在接下来的状况下也不是最优的，所以
可以直接淘汰。

而所谓的单调队列优化其实也是这样，就是在队列里维护可能提供最优值的那些状态，
不断的插入新的点，不断的删掉不符合或者不优的点；
然后在维护的队列里快速的找到那个使当前状态最优的那个状态；

 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<vector>
 #include<set>
 using namespace std;
 const int N=+;
 typedef long long LL;
 struct Point{
     LL x,y;
     Point (LL a=,LL b=):x(a),y(b){}
     Point operator - (const Point &p) const{
         return Point(x-p.x,y-p.y);
     }
 };
 typedef Point Vector;
 inline LL Cross(const Vector &u,const Vector &v){
     return u.x*v.y - u.y*v.x;
 }
 int n,M;
 struct dequeue{
     Point q[N];
     int head,tail;
     void init(){
         head = ; tail = ;
     }
     void push(const Point &u){
         while (head < tail && Cross(q[tail]-q[tail-],u-q[tail-]) <=  ) tail--;
         q[++tail] = u;
     }
     Point pop(const LL &k){//斜率的大小
         while (head < tail && k*q[head].x + q[head].y >= k*q[head+].x + q[head+].y ) head++;
         return q[head];
     }
 }H;
 // dp[i] = -k*x[j] + y[j] + w;
 // 写成结构体常数比较大;
 void solve(){

     H.init();
     //队列里初始值得看情况,比如H.push(Point(0,0));
     for (int i=;i<=n;i++){
         Point t = H.pop(k);
         dp[i] = -k*t.x + t.y + W;
         H.push(Point(x[i],y[i]));
     }
 }

还有就是不满足单调的，首先是
斜率不满足单调性，x[i],y[i]还是满足单调；
这样凸包还是可以直接维护的，但是找凸包上的点就不能在o(1)的时间找到；
但是我们可以用三分找，因为按照队列里点的顺序G值是先变小后变大的；

也可以二分斜率，因为在凸包上相邻两个点的斜率是单调递增的；

     用find()代替pop();
     int find(const LL &k){
         int l = head, r = tail;
         while (r - l >= ){
             int m1 = l + (r-l)/;
             int m2 = r - (r-l)/;
             if (k*q[m1].x+q[m1].y >= k*q[m2].x+q[m2].y ) l = m1+;
             else r = m2-;
         }
         int ret = l;
         for (int i = l+; i <= r; i++) {
             if (k*q[i].x+q[i].y <= k*q[ret].x+q[ret].y) ret = i;
         }
         return ret;
     }

然后如果x[i],y[i]也不满足单调，这样就不能直接维护凸包了，需要动态维护凸包
简单点的就是用set,但是set无法实现kth大，所以得自己写平衡树；

先找到插入点前驱，和后继（水平序），然后分两边同时维护凸包，（如果还不太清楚可以看一下本博客的动态凸包的代码）

再用三分找最小；

要用到的就是findPre(),findNext(),kth();当然也可以在插入的时候记录下该点跟前驱的斜率，然后

直接查找第一个比读入斜率大的点就可以，因为在平衡树里斜率也是满足二叉树的性质的，这样就不用kth()了，

代码可以参看hust里；

因为一个点被删除后就不会在进入凸包，时间O(logn),查找要logn;
所以总时间复杂度为O(logn*logn*n)；

http://acm.hust.edu.cn/vjudge/problem/viewProblem.action?id=31649

货币兑换：splay  dp[i] = ai[i]*x[j]+bi[i]*y[j] ----->  dp[i]/bi[i] = ai[i]/bi[i] *x[j] +y[j];

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<vector>
 #include<cstdlib>
 using namespace std;
 const int N=+;
 const  double eps=1e-;
 inline int dcmp(double x){
     return x<-eps ? - : x>eps;
 }
 struct Point{
     double x,y;
     Point(double a=,double b=):x(a),y(b){}
     Point operator - (const Point &p)const{
         return Point(x-p.x,y-p.y);
     }
     double operator * (const Point &p)const{
         return x*p.y - y*p.x;
     }
     bool operator < (const Point &p)const{
         return dcmp(x-p.x)< || (dcmp(x-p.x)== && dcmp(y-p.y)<);
     }
 };
 struct splay_tree{
     int sz,root,ch[N][],pre[N],ss[N];
     Point val[N];
     void rotate(int x){
         int y = pre[x];
         int f = (ch[y][]==x);
         ch[y][f^] = ch[x][f];
         pre[ ch[x][f] ] = y;
         pre[ x ] = pre[ y ];
         ch[ pre[y] ][ ch[ pre[y] ][  ] == y ] = x;
         ch[x][f] = y;
         pre[y] = x;
         pushup(y);
     }
     void splay(int x,int goal){
         while (pre[x] != goal ){
             int y = pre[x], z = pre[y];
             if (z==goal){
                 rotate(x);
             }else {
                 int f = (ch[z][]==y);
                 if (ch[y][f] == x){
                     rotate(x); rotate(x);
                 }else {
                     rotate(y); rotate(x);
                 }
             }
         }
         pushup(x);
         if (goal == ) root=x;
     }
     void init(){
         sz=; ch[][]=ch[][]=pre[]=; val[]=Point(,); ss[]=;
     }
     void pushup(int x){
         ss[x] = ss[ ch[x][] ] + ss[ ch[x][] ] + ;
     }
     void insert(Point x){
         val[++sz]=x; ss[sz]=;
         ch[sz][]=ch[sz][]=pre[sz]=;
         if (sz==){
             root=; return;
         }
         int u,f;
         for (u=root; ch[u][f=val[u]<x]; u=ch[u][f]);
         ch[u][f] = sz;
         pre[sz] = u;
         splay(sz,);
         if (sz<=) return;
         ins(sz);
     }
     void remove(int x){
         int u = findPre(x), v = findNext(x);
         splay(u,); splay(v,u);
         ch[v][]=;
         splay(v,);
     }
     int findPre(int x){
         splay(x,);
         int u;
         if (ch[x][]==) return ;
         for (u=ch[x][]; ch[u][]; u=ch[u][]);
         return u;
     }
     int findNext(int x){
         splay(x,);
         int u;
         if (ch[x][]==) return ;
         for (u=ch[x][]; ch[u][]; u=ch[u][]);
         return u;
     }
     void ins(int x){
         int u = findPre(x), v = findNext(x);
         if (u!= && v!=) {
             double k= (val[u]-val[x])*(val[v]-val[x]);
             if (dcmp(k)<=) {
                 remove(x); return;
             }
         }
         while (){
             u=findNext(x);
             if (u==) break;
             v=findNext(u);
             if (v==) break;
             double k=(val[u]-val[x])*(val[v]-val[x]);
             if (dcmp(k)>=){
                 remove(u);
             }else break;
         }
         while (){
             u=findPre(x);
             if (u==) break;
             v=findPre(u);
             if (v==) break;
             double k=(val[u]-val[x])*(val[v]-val[x]);
             if (dcmp(k)<=){

                 remove(u);
             }else break;
         }
     }
     int kth(int k){
         int tmp=k;
         if (k>ss[root]) return ;
         int x = root;
         while (ss[ ch[x][] ]+!=k){
             int c = ss[ ch[x][] ];
             if (k<=c) x = ch[x][];
             else {
                 x = ch[x][];
                 k -= c+;
             }
         }
         splay(x,);
         return x;
     }
     double cal(double k,int x){
         return k*val[x].x+val[x].y;
     }
     Point find(double k){
         int l=,r=ss[root];
         while (r-l>){
             int m1= l+(r-l)/;
             int m2= r-(r-l)/;
             if (cal(k,kth(m1))>cal(k,kth(m2))) r=m2-;
             else l=m1+;
         }
         int ret=kth(l);
         double tmp=cal(k,ret);
         for (int i=l+;i<=r;i++){
             int t=kth(i);
             double t2=cal(k,t);
             if (tmp<t2) {
                 ret=t; tmp=t2;
             }
         }
         return val[ret];
     }
     void debug(){
         printf("root: %d\n",root);print_tree(root);
     }
     void print_tree(int x){
         if (x){
             print_tree(ch[x][]);
             printf("now: %d ,fa: %d ,son0: %d ,son1: %d ,size: %d\n",x,pre[x],ch[x][],ch[x][],ss[x]);
             print_tree(ch[x][]);
         }

     }
 }H;
 int n,s;
 double ak[N],bk[N],rk[N];
 double dp[N];
 void solve(){
     H.init();
     double x,y;
     dp[]=s;
     y = (double)s/(rk[]*ak[]+bk[]);
     x = rk[]*y;
     H.insert(Point(x,y));
     for (int i=;i<=n;i++){
         Point t = H.find(ak[i]/bk[i]);
         dp[i] =max(dp[i-], ak[i]*t.x+bk[i]*t.y);
         y = dp[i]/(rk[i]*ak[i]+bk[i]);
         x = rk[i]*y;
         H.insert(Point(x,y));
     }
     printf("%.3lf\n",dp[n]);
 }
 int main(){
 //    freopen("in.txt","r",stdin);
 //    freopen("1.out","w",stdout);
     while (~scanf("%d%d",&n,&s)){
         for (int i=;i<=n;i++) scanf("%lf%lf%lf",&ak[i],&bk[i],&rk[i]);
         solve();
     }

     return ;
 }

这样对于形如 DP[i] = min/max(-a[i]*x[j]+y[j])+w[i]; (1<=j<i)
的DP方程都可以解决了；