线性回归（linear regression）

基本形式

最小二乘法估计拟合参数

最小二乘法：基于均方误差最小化来进行模型求解的方法称为“最小二乘法”（least square method）

　　　　　　即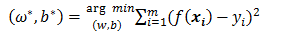（左边代表 $\mathbf{\omega }$ 和 b 的解）

为了计算的方便，可以把常数 b 看出一个特殊的值为 1 的 x 。

将 $\mathbf{\omega }$ 和 b 吸收入向量形式，如下所示：

$X = \begin{pmatrix}
x_{11} &x_{12} &... &x_{1d} &1\\
x_{21} &x_{2} &... &x_{2d} &1\\
\vdots &\vdots &\ddots &\vdots &\vdots \\
x_{m1} &x_{m2} &... &x_{md} &1
\end{pmatrix} = \begin{pmatrix}
\mathbf{x_{1}^{T}}& 1\\
\mathbf{x_{2}^{T}}&1 \\
\vdots & \vdots \\
\mathbf{x_{m}^{T}}& 1
\end{pmatrix}$

把标记也写成向量形式$\mathbf{y}=(y_{1};y_{2};...;y_{m})$，则参数的求解为：

$ \hat{\mathbf{\omega} }^{*}=_{\hat{\mathbf{\omega} }}^{arg\ min}\  \textrm{}(\mathbf{y}-\mathbf{X}\hat{\mathbf{\omega} })^{T}(\mathbf{y}-\mathbf{X\hat{\mathbf{\omega} }})$

令$E_{\hat{\mathbf{\omega} }}=(\mathbf{y}-\mathbf{X}\hat{\mathbf{\omega} })^{T}(\mathbf{y}-\mathbf{X\hat{\mathbf{\omega} }})$，对$\hat{\mathbf{\omega} }$求导得到：

$\frac{\partial E_{\hat{\mathbf{\omega} }}}{\partial\hat{\mathbf{\omega} }} = 2\mathbf{X}^{T}(\mathbf{X\hat{\mathbf{\omega} }-\mathbf{y}})$

要得到这个求导结果，需要知道一些矩阵求导的常见性质：

$f(x)=Ax,则\frac{\partial f(x)}{\partial x^{T}}=\frac{\partial (Ax)}{\partial x^{T}}=A$

$f(x)=x^{T}Ax,则\frac{\partial f(x)}{\partial x}=\frac{\partial (x^{T}Ax)}{\partial x}=Ax+A^{T}x$

$f(x)=a^{T}x,则\frac{\partial f(x)}{\partial x}=\frac{\partial (a^{T}x)}{\partial x}=\frac{\partial x^{T}a}{\partial x}=a$

令上式为0即可得参数的最优解，由于涉及到矩阵逆计算，所有只有当$\mathbf{X}^{T}\mathbf{X})^{-1}$为满秩矩阵或正定矩阵才可以得到如下结果：

$\hat{\mathbf{\omega} }^{*}=(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{y}$

简单例子

该例子来自《机器学习实战》。

数据如下：

这里第一列均为1，目的就是将式子中的b转化为1。

首先可以绘制图形大致观察一下：

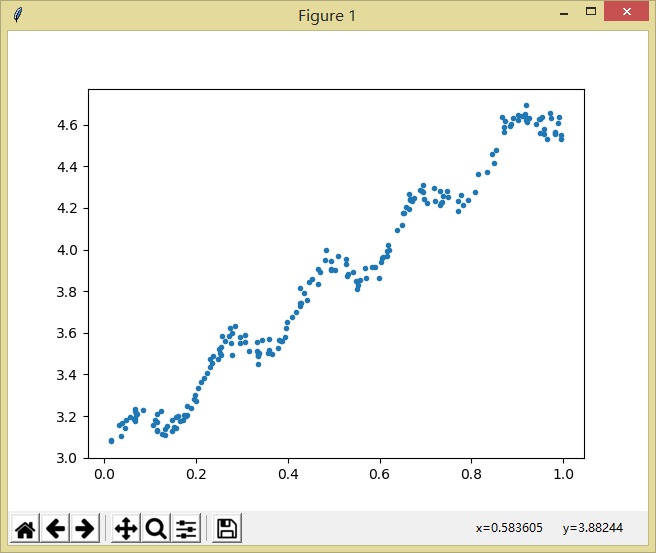
只要明白上面的，计算参数其实很简单，代码如下：

 import numpy as np

 def load_data_set(filename):    # 数据导入
     fr = open(filename)
     num_feat = len(open(filename).readline().split('\t'))-1

     data_mat = []
     label_mat = []

     for line in fr.readlines():
         line_arr = []
         cur_line = line.strip().split('\t')
         for i in range(num_feat):
             line_arr.append(float(cur_line[i]))

         data_mat.append(line_arr)
         label_mat.append(float(cur_line[-1]))
     return data_mat, label_mat

 def stand_regress(x_arr, y_arr):  # 计算拟合参数
     x_mat = np.mat(x_arr)
     y_mat = np.mat(y_arr).T
     xtx = x_mat.T * x_mat
     if np.linalg.det(xtx) == 0:
         print("This matrix is singular, cannot do inverse")
         return
     ws = xtx.I * x_mat.T * y_mat
     return ws    # 返回最后得到的参数值

第一个函数打开用tab分隔的文本文件，提取出其中的数据。

第二个函数计算最佳拟合直线，代码中numpy的linalg.det()可以计算行列式的值。计算的公式直接套用上面所讲的最终公式即可。

最后得到的参数值为：