FSM（状态机）、HFSM（分层状态机）、BT（行为树）的区别

游戏人工智能AI中最常听见的就是这三个词拉：

FSM

这个不用说拉，百度一大堆解释，

简单将就是将游戏AI行为分为一个一个的状态，状态与状态之间的过渡通过事件的触发来形成。

比如士兵的行为有“巡逻”，“追击敌人”，“攻击敌人”，“逃跑”等行为，

响应的事件就有“发现敌人”，“追到敌人”，“敌人逃跑”，“敌人死亡”，“自己血量不足”等。

那么可以写成这样一个状态机：

1.士兵 “巡逻”，如果 “发现敌人”，那么，“追击敌人”

2.士兵 “追击敌人”， 如果 “追到敌人”， 那么，“攻击敌人”

3.士兵 “追击敌人”， 如果 “敌人死亡”， 那么，继续 “巡逻”

4.士兵 “攻击敌人”， 如果 “敌人死亡”， 那么，继续 “巡逻”

5.士兵 “攻击敌人”， 如果 “血量不足”， 那么，“逃跑”

其中，士兵就是这个FSM的执行者，红色的就是状态，蓝色的就是事件，

整个状态机的行为可以总结为：

当前状态=>是否满足条件1，如果是，则跳转到对应状态

　　否则=>是否满足条件2，如果是，则跳转到对应状态

由此可看出，状态机是一种“事件触发型”AI，就是只有事件的触发才会发生引起状态的变化。

HFSM

简单来说，就是FSM当状态太多的时候，不好维护，于是将状态分类，抽离出来，将同类型的

状态做为一个状态机，然后再做一个大的状态机，来维护这些子状态机。

举个决策小狗行为的例子：

我们对小狗定义了有很多行为，比如跑，吃饭，睡觉，咆哮，撒娇，摇尾巴等等，如果每个行为都是一个状态，

用常规状态机的话，我们就需要在这些状态间定义跳转，比如在“跑”的状态下，如果累了，那就跳转到“睡觉”状态，

再如，在“撒娇”的状态下，如果感到有威胁，那就跳转到“咆哮”的状态等等，我们会考量每一个状态间的关系，定

义所有的跳转链接，建立这样一个状态机。如果用层次化的状态机的话，我们就先会把这些行为“分类”，把几个小状

态归并到一个状态里，然后再定义高层状态和高层状态中内部小状态的跳转链接。

其实层次化状态机从某种程度上，就是限制了状态机的跳转，而且状态内的状态是不需要关心外部状态的跳转的，

这样也做到了无关状态间的隔离，比如对于小狗来说，我们可以把小狗的状态先定义为疲劳，开心，愤怒，然后这些

状态里再定义小状态，比如在开心的状态中，有撒桥，摇尾巴等小状态，这样我们在外部只需要关心三个状态的跳

转（疲劳，开心，愤怒），在每个状态的内部只需要关心自己的小状态的跳转就可以了。这样就大大的降低了状态机的复杂度，

另外，如果觉得两层的状态机还是状态太多的话，可以定义更多的状态层次以降低跳转链接数。

（摘自此文章）

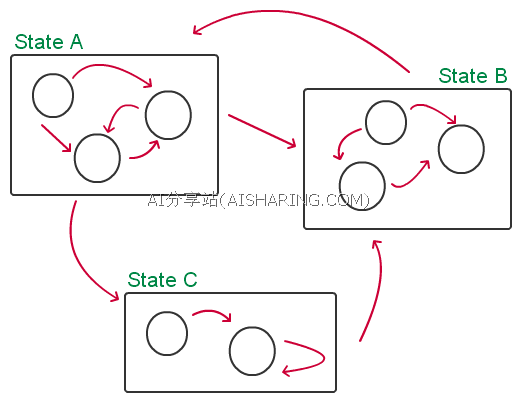
Behavir Tree

有空再更新，先看之前的文章：http://www.cnblogs.com/jeason1997/p/4803243.html

行为树与FSM不同，它是一种“轮询式机制”，即每次更新都会遍历树，判定逻辑是否成立，是否该继续往下执行。