POJ-3067 Japan---树状数组逆序对变形

题目链接：

https://vjudge.net/problem/POJ-3067

题目大意：

日本岛东海岸与西海岸分别有N和M个城市，现在修高速公路连接东西海岸的城市，求交点个数。

解题思路：

记每条告诉公路为(x,y), 即东岸的第x个城市与西岸的第y个城市修一条路。当两条路有交点时，满足（x1-x2）*（y1-y2） < 0。所以，将每条路按x从小到达排序，若x相同，按y从小到大排序。 然后按排序后的公路用树状数组在线更新，求y的逆序数之和 即为交点个数。

比如样例

1 4
2 3
3 2
3 1

排完序后

1 4
2 3
3 1
3 2

1、加入1 4，此时比4大的元素为0，交点数目为0

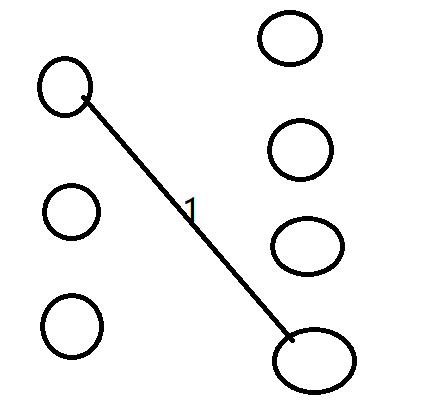
2、加入2 3，此时比3大的元素数目为1，交点数目为1

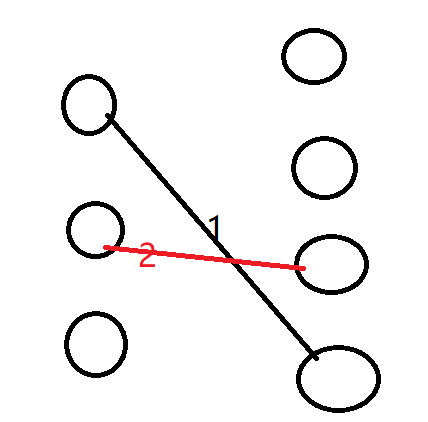
3、加入3 1，此时比1大的数字有两个，交点数目为3

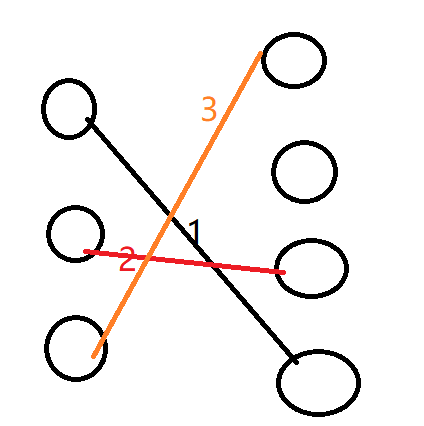
4、加入3 2，此时比2大的数字有2个，交点数目为5

如果先加人3 2，再加入3 1的话会导致3 1这条计算交点的时候吧3 2算进去，但实际上并没有交点，所以排序顺序在x相同的y从小到大排序

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<string>
 #include<map>
 #include<set>
 #include<cmath>
 #include<algorithm>
 using namespace std;
 typedef long long ll;
 const int maxn =  + ;
 int n, m, T, k, cases;
 struct node
 {
     int x, y;
     bool operator <(const node& a)const
     {
         return x < a.x || x == a.x && y < a.y;
     }
 };
 node a[maxn];
 int tree[];
 int lowbit(int x)
 {
     return x & (-x);
 }
 ll sum(int x)
 {
     ll ans = ;
     while(x)
     {
         ans += tree[x];
         x -= lowbit(x);
     }
     return ans;
 }
 void add(int x, int d)
 {
     while(x <= m)
     {
         tree[x] += d;
         x += lowbit(x);
     }
 }
 int main()
 {
     cin >> T;
     while(T--)
     {
         cin >> n >> m >> k;
         memset(tree, , sizeof(tree));
         for(int i = ; i <= k; i++)
         {
             scanf("%d%d", &a[i].x, &a[i].y);
         }
         sort(a + , a +  + k);
         ll ans = ;
         for(ll i = ; i <= k; i++)
         {
             add(a[i].y, );
             ans += (i - sum(a[i].y));
         }
         printf("Test case %d: %lld\n", ++cases, ans);
     }
     return ;
 }