计算1到n的n次方之和

实现效果：

　　

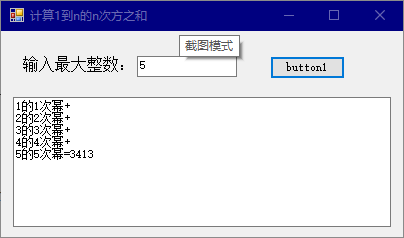
知识运用：
　　Math类的Pow方法:返回指定数字的指定次幂

　　public static double Pow(double x,double y)

实现代码：

        public string sum(int num) {
            string result = "";
            double sum = 0;
            for (int i = 1; i <= num;i++ )
            {
                sum += Math.Pow(i,i);
                result += i + "的" + i + "次幂" + "+"+Environment.NewLine;
            }
            return result.Substring(0,result.Length-3)+"="+sum;
        }