DFS算法模板(2488:A Knight's Journey)
DFS算法(C++版本)
题目一:
链接:http://bailian.openjudge.cn/practice/2488/

解析思路:
骑士找路就是基本的DFS,用递归不断找到合适的路,找不到就回头直到找到合适的路。
该题难点:要是实现字典序,也就是同样的两种选择,要走到A1而不是B1。所以就有了{-1,-2},{1,-2},{-2,-1},{2,-1},{-2,1},{2,1},{-1,2},{1,2}寻路时走路的尝试走路顺序。注意:我的程序输入的行(m)是表示的数字,列(n)表示的是字母这也是为什么尝试走路的顺序是列小的排在前面优先选择。
代码思路:
根据每次输入的m和n构建棋盘,visit数组默认是全为0,visit数组是棋盘的位置是1,然后经过DFS,走过的棋盘点在visit数组对应的位置置为2,不走走过的棋盘点也就是visit数组是2的点。用road数组记录如果成功走完了棋盘的路径,如果road数组的元素个数不等于m*n(棋盘点的个数),输出impossible,否则输出road数组。完工!!!!!!!!!!!!!!!!!!!
代码实现:
#include<iostream>
#include<cstring>
using namespace std;
//骑士之旅 http://bailian.openjudge.cn/practice/2488/
//右(上)上 {1,2} 右(下)上 {2,1}
//右(上)下 {2,-1} 右(下)下 {1,-2}
//左(上)上 {-1,2} 左(下)上 {-2,1}
//左(上)下 {-2,-1} 左(下)下 {-1,-2}
char alf[27] = { '0','A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z' };
int number[10] = { 0,1,2,3,4,5,6,7,8,9 };
int visit[11][11];//棋盘点 1表示棋盘 2走过的棋盘点
int road[40];//走的路线 十位表示行 个位表示列
int freq;//用于记录有多少次的输出
int step = 0; //走过了多少步
char re_sign;//0表示没走到头 1表示走到头了
void ways(int i, int j, int m, int n)
{
//走过的路
visit[i][j] = 2;
road[step++] = (i + 1) * 10 + (j + 1);//除去i和j为0的情况
//走通了
if (step == m * n)
{
re_sign = 1;
return;
}
//走路的操作
// 数字+字母 字母的字典序优先(A7>B1)
//{-1,-2},{1,-2},{-2,-1},{2,-1},{-2,1},{2,1},{-1,2},{1,2}
if (i - 1 >= 0 && j - 2 >= 0 && visit[i - 1][j - 2] == 1)
ways(i - 1, j - 2, m, n);
if (i + 1 < m && j - 2 >= 0 && visit[i + 1][j - 2] == 1)
ways(i + 1, j - 2, m, n);
if (i - 2 >= 0 && j - 1 >= 0 && visit[i - 2][j - 1] == 1)
ways(i - 2, j - 1, m, n);
if (i + 2 < m && j - 1 >= 0 && visit[i + 2][j - 1] == 1)
ways(i + 2, j - 1, m, n);
if (i - 2 >= 0 && j + 1 < n && visit[i - 2][j + 1] == 1)
ways(i - 2, j + 1, m, n);
if (i + 2 < m && j + 1 < n && visit[i + 2][j + 1] == 1)
ways(i + 2, j + 1, m, n);
if (i - 1 >= 0 && j + 2 < n && visit[i - 1][j + 2] == 1)
ways(i - 1, j + 2, m, n);
if (i + 1 < m && j + 2 < n && visit[i + 1][j + 2] == 1)
ways(i + 1, j + 2, m, n);
if (re_sign == 1)
{
return;
}
//路走不通,把road还原(waiting)
visit[i][j] = 1;//恢复棋盘点
road[--step] = 0;//把原来记录走路的点恢复,再Sn减1==现走了几步
}
int main()
{
//要将要输入几组数据
int t;
cin >> t;
while (t--)
{
int m, n;
cin >> m >> n;// m 字母(A B C D) n 数字(1 2 3 4)
cout << "Scenario #" << ++freq << ":" << endl; //打印序号
if (m == 0 && n == 0)//输入错误信息
{
cout << "这样子的棋盘不存在" << endl;
continue;
}
//初始化
step = 0;
re_sign = 0;
memset(road, 0, sizeof(road));
memset(visit, 0, sizeof(visit));
//只考虑在A1开始寻路的情况
for (int i = 0; i < m; ++i)
{
for (int j = 0; j < n; ++j)
{
visit[i][j] = 1;
}
}
ways(0, 0, m, n);//起始点开始DFS
//结果输出
if (step == m * n)
{
for (int i = 0; i < step; i++)
{
//输出走过的路
cout << alf[road[i] % 10] << number[road[i] / 10];
}
cout << endl<<endl;
}
else
{
cout << "impossible"<<endl<<endl;
}
}
}
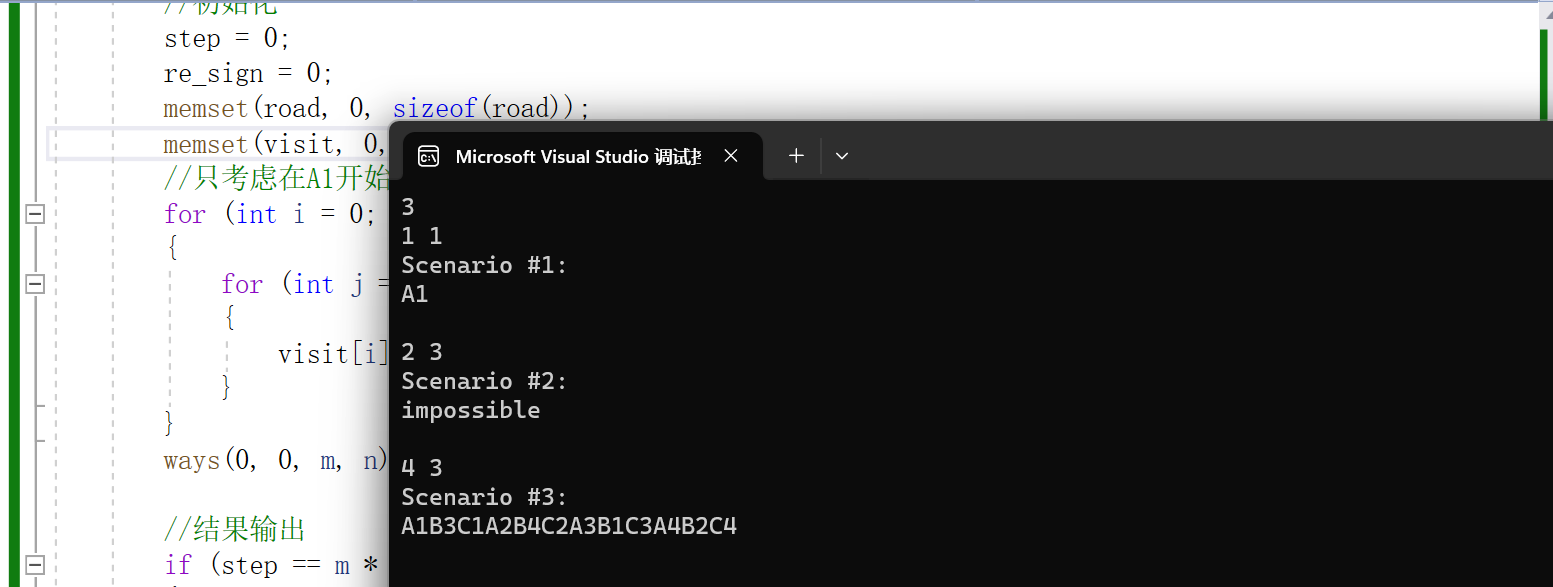
运行结果:
DFS算法模板(2488:A Knight's Journey)的更多相关文章
- POJ 2488 -- A Knight's Journey(骑士游历)
POJ 2488 -- A Knight's Journey(骑士游历) 题意: 给出一个国际棋盘的大小,判断马能否不重复的走过所有格,并记录下其中按字典序排列的第一种路径. 经典的“骑士游历”问题 ...
- DFS 算法模板
dfs算法模板: 1.下一层是多节点的dfs遍历 def dfs(array or root, cur_layer, path, result): if cur_layer == len(array) ...
- POJ 2488 A Knight's Journey(DFS)
A Knight's Journey Time Limit: 1000MSMemory Limit: 65536K Total Submissions: 34633Accepted: 11815 De ...
- POJ 2488 A Knight's Journey(深搜+回溯)
A Knight's Journey Time Limit : 2000/1000ms (Java/Other) Memory Limit : 131072/65536K (Java/Other) ...
- DFS算法(——模板习题与总结)
首先,需要说明的是搜索算法本质上也是枚举的一种,时间复杂度还是很高的,遇到问题(特别是有水平的比赛上),不要优先使用搜索算法. 这里总结一下DFS算法: 1.从图中某个顶点出发,访问v. 2.找出刚访 ...
- [poj]2488 A Knight's Journey dfs+路径打印
Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 45941 Accepted: 15637 Description Bac ...
- poj 2488 A Knight's Journey( dfs )
题目:http://poj.org/problem?id=2488 题意: 给出一个国际棋盘的大小,判断马能否不重复的走过所有格,并记录下其中按字典序排列的第一种路径. #include <io ...
- poj 2488 A Knight's Journey 【骑士周游 dfs + 记忆路径】
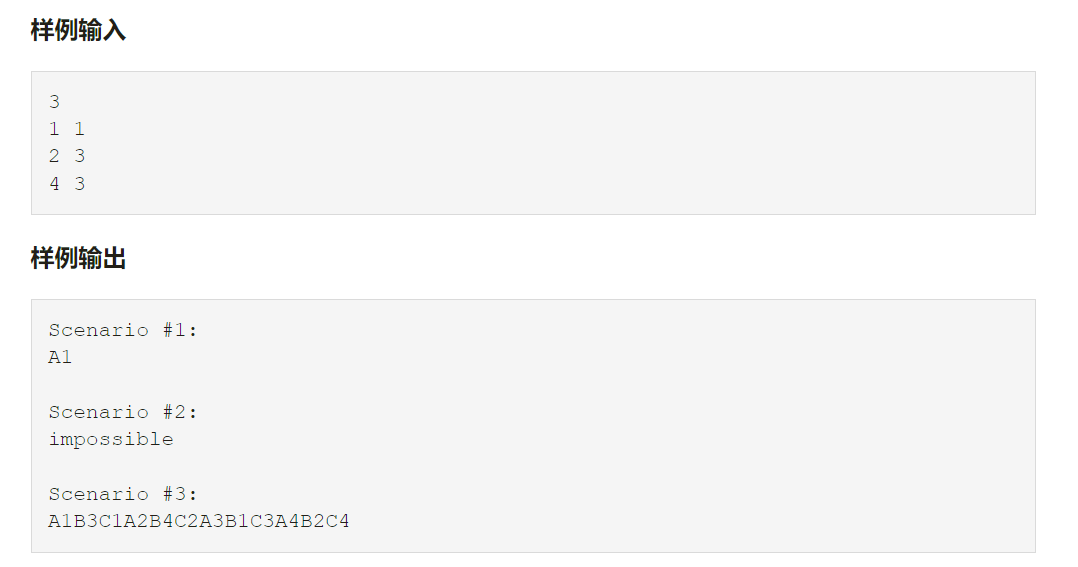
题目地址:http://poj.org/problem?id=2488 Sample Input 3 1 1 2 3 4 3 Sample Output Scenario #1: A1 Scenari ...
- POJ 2488 A Knight's Journey【DFS】
补个很久之前的题解.... 题目链接: http://poj.org/problem?id=2488 题意: 马走"日"字,让你为他设计一条道路,走遍所有格,并输出字典序最小的一条 ...
- POJ 2488 A Knight's Journey (DFS)
poj-2488 题意:一个人要走遍一个不大于8*8的国际棋盘,他只能走日字,要输出一条字典序最小的路径 题解: (1)题目上说的"The knight can start and end ...
随机推荐
- Redis内存问题的学习之一
Redis内存问题的学习之一 背景 前几天帮同事看redis的问题 发现info memory 显示 60GB 但是实际上 save出来的dump文件只有 800M 然后导入到其他的redis之后, ...
- [转帖]SQL中 join 、in 、exists 使用场景和执行效率
https://www.jianshu.com/p/c825c9bf42c2 众所周知,在sql 中,join /in /exists 都可以用来实现,"查询A表中在(或者不在)B表中的记录 ...
- [转帖]从理论到实践,异步I/O模式下NVMe SSD高性能之道
在早期NVMe的讨论话题中,常常将之AHCI协议进行对比,在支持的最大队列深度.并发进程数以及消耗时钟周期数等方面,NVMe吊打了AHCI.最直观也最权威的就是下面这张对比图片. NVMe与AHCI协 ...
- [转帖]021系统状态检测命令sosreport
https://www.cnblogs.com/anyoneofus/p/16467677.html sosreport命令用于收集系统配置及架构信息并输出诊断文档.
- [转帖]Linux下的I/O复用与epoll详解
https://blog.csdn.net/weixin_39094034/article/details/110393127 前言 I/O多路复用有很多种实现.在linux上,2.4内核前主要是se ...
- [转帖]/etc/profile和/etc/environment的区别
时间 2019-11-07 标签 profile environment 区别 繁體版 原文 https://my.oschina.net/u/2885925/blog/2989579 /etc ...
- [转帖]谈 JVM 参数 GC 线程数 ParallelGCThreads 合理性设置
https://my.oschina.net/u/4090830/blog/7926038 1. ParallelGCThreads 参数含义 在讲这个参数之前,先谈谈 JVM 垃圾回收 (GC) 算 ...
- 如何给所有的 await async 函数添加try/catch?
如何给所有的 await async 函数添加try/catch?做全局捕获异常. 面试官:如何给所有的 await async 函数添加try/catch?做全局捕获异常. 我们可以使用 windo ...
- Redis做Mybatis的二级缓存
Redis做mybatis的二级缓存 作用提升速度,保证多台服务器访问同一数据库时不会崩 注意:保证本地有下载redis且已经打开,否则无法使用. [本文只讲述了实现步骤,并没有原理讲解] 保证有导入 ...
- 【K哥爬虫普法】辛苦钱被中间商抽走八成,还因此锒铛入狱
我国目前并未出台专门针对网络爬虫技术的法律规范,但在司法实践中,相关判决已屡见不鲜,K 哥特设了"K哥爬虫普法"专栏,本栏目通过对真实案例的分析,旨在提高广大爬虫工程师的法律意识, ...
