基于tensorflow的RBF神经网络案例

1 前言

在使用RBF神经网络实现函数逼近中，笔者介绍了使用 Matlab 训练RBF神经网络。本博客将介绍使用 tensorflow 训练RBF神经网络。代码资源见：RBF案例（更新版）

这几天，笔者在寻找 tensorflow 中 RBF 官方案例，没找到，又看了一些博客，发现这些博客或不能逼近多元函数，或不能批量训练。于是，自己手撕了一下代码。

RBF神经网络中需要求解的参数有4个：基函数的中心和方差、隐含层到输出层的权值和偏值。

RBF 神经网络的关键在于中心的选取，一般有如下三种方法：

• 直接计算法：直接通过先验经验固定中心，并计算方差，再通过有监督学习得到其他参数
• 自组织学习法：先通过k-means等聚类算法求出中心（无监督学习），并计算方差，再通过有监督学习得到其他参数
• 有监督学习法：直接通过有监督学习求出所有参数

在直接计算法和自组织学习法中，方差的计算公式如下：

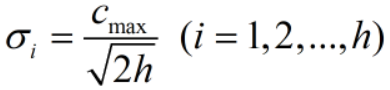
其中 Cmax 表示 h 个中心间的最大距离。

本博客主要介绍后两种中心计算方法实现 RBF 神经网络。

笔者工作空间如下：

2 RBF神经网络实现

2.1 自组织学习选取RBF中心

RBF_kmeans.py

import tensorflow as tf
import numpy as np
from sklearn.cluster import KMeans

class RBF:
    #初始化学习率、学习步数
    def __init__(self,learning_rate=0.002,step_num=10001,hidden_size=10):
        self.learning_rate=learning_rate
        self.step_num=step_num
        self.hidden_size=hidden_size

    #使用 k-means 获取聚类中心、标准差
    def getC_S(self,x,class_num):
        estimator=KMeans(n_clusters=class_num,max_iter=10000) #构造聚类器
        estimator.fit(x) #聚类
        c=estimator.cluster_centers_
        n=len(c)
        s=0;
        for i in range(n):
            j=i+1
            while j<n:
                t=np.sum((c[i]-c[j])**2)
                s=max(s,t)
                j=j+1
        s=np.sqrt(s)/np.sqrt(2*n)
        return c,s

    #高斯核函数(c为中心，s为标准差)
    def kernel(self,x,c,s):
        x1=tf.tile(x,[1,self.hidden_size]) #将x水平复制 hidden次
        x2=tf.reshape(x1,[-1,self.hidden_size,self.feature])
        dist=tf.reduce_sum((x2-c)**2,2)
        return tf.exp(-dist/(2*s**2))

    #训练RBF神经网络
    def train(self,x,y):
        self.feature=np.shape(x)[1] #输入值的特征数
        self.c,self.s=self.getC_S(x,self.hidden_size) #获取聚类中心、标准差

        x_=tf.placeholder(tf.float32,[None,self.feature]) #定义placeholder
        y_=tf.placeholder(tf.float32,[None,1]) #定义placeholder

        #定义径向基层
        z=self.kernel(x_,self.c,self.s)  

        #定义输出层
        w=tf.Variable(tf.random_normal([self.hidden_size,1]))
        b=tf.Variable(tf.zeros([1]))
        yf=tf.matmul(z,w)+b

        loss=tf.reduce_mean(tf.square(y_-yf))#二次代价函数
        optimizer=tf.train.AdamOptimizer(self.learning_rate) #Adam优化器
        train=optimizer.minimize(loss) #最小化代价函数
        init=tf.global_variables_initializer() #变量初始化

        with tf.Session() as sess:
            sess.run(init)
            for epoch in range(self.step_num):
                sess.run(train,feed_dict={x_:x,y_:y})
                if epoch>0 and epoch%500==0:
                    mse=sess.run(loss,feed_dict={x_:x,y_:y})
                    print(epoch,mse)
            self.w,self.b=sess.run([w,b],feed_dict={x_:x,y_:y})

    def kernel2(self,x,c,s): #预测时使用
        x1=np.tile(x,[1,self.hidden_size]) #将x水平复制 hidden次
        x2=np.reshape(x1,[-1,self.hidden_size,self.feature])
        dist=np.sum((x2-c)**2,2)
        return np.exp(-dist/(2*s**2))

    def predict(self,x):
        z=self.kernel2(x,self.c,self.s)
        pre=np.matmul(z,self.w)+self.b
        return pre

2.2 有监督学习选取RBF中心

RBF_Supervised.py

import numpy as np
import tensorflow as tf

class RBF:
    #初始化学习率、学习步数
    def __init__(self,learning_rate=0.002,step_num=10001,hidden_size=10):
        self.learning_rate=learning_rate
        self.step_num=step_num
        self.hidden_size=hidden_size

    #高斯核函数(c为中心，s为标准差)
    def kernel(self,x,c,s): #训练时使用
        x1=tf.tile(x,[1,self.hidden_size]) #将x水平复制 hidden次
        x2=tf.reshape(x1,[-1,self.hidden_size,self.feature])
        dist=tf.reduce_sum((x2-c)**2,2)
        return tf.exp(-dist/(2*s**2))

    #训练RBF神经网络
    def train(self,x,y):
        self.feature=np.shape(x)[1] #输入值的特征数
        x_=tf.placeholder(tf.float32,[None,self.feature]) #定义placeholder
        y_=tf.placeholder(tf.float32,[None,1]) #定义placeholder

        #定义径向基层
        c=tf.Variable(tf.random_normal([self.hidden_size,self.feature]))
        s=tf.Variable(tf.random_normal([self.hidden_size]))
        z=self.kernel(x_,c,s)

        #定义输出层
        w=tf.Variable(tf.random_normal([self.hidden_size,1]))
        b=tf.Variable(tf.zeros([1]))
        yf=tf.matmul(z,w)+b

        loss=tf.reduce_mean(tf.square(y_-yf))#二次代价函数
        optimizer=tf.train.AdamOptimizer(self.learning_rate) #Adam优化器
        train=optimizer.minimize(loss) #最小化代价函数
        init=tf.global_variables_initializer() #变量初始化

        with tf.Session() as sess:
            sess.run(init)
            for epoch in range(self.step_num):
                sess.run(train,feed_dict={x_:x,y_:y})
                if epoch>0 and epoch%500==0:
                    mse=sess.run(loss,feed_dict={x_:x,y_:y})
                    print(epoch,mse)
            self.c,self.s,self.w,self.b=sess.run([c,s,w,b],feed_dict={x_:x,y_:y})

    def kernel2(self,x,c,s): #预测时使用
        x1=np.tile(x,[1,self.hidden_size]) #将x水平复制 hidden次
        x2=np.reshape(x1,[-1,self.hidden_size,self.feature])
        dist=np.sum((x2-c)**2,2)
        return np.exp(-dist/(2*s**2))

    def predict(self,x):
        z=self.kernel2(x,self.c,self.s)
        pre=np.matmul(z,self.w)+self.b
        return pre

3 案例

3.1 一元函数逼近

待逼近函数：

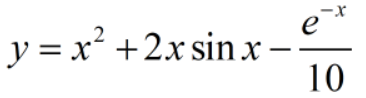
（1）自组织学习选取RBF中心

test_kmeans.py

import numpy as np
import matplotlib.pyplot as plt
from RBF_kmeans import RBF

#待逼近的函数
def fun(x):
    return x*x+2*x*np.sin(x)-np.exp(-x)/10

#生成样本
def generate_samples():
    n=150 #样本点个数
    wideX=0.03 #横轴噪声的宽度
    wideY=0.5 #纵轴噪声宽度
    t=np.linspace(-5,5,n).reshape(-1,1) #横轴理想值
    u=fun(t) #纵轴理想值
    noisyX=np.random.uniform(-wideX,wideX,n).reshape(n,-1) #横轴噪声
    noisyY=np.random.uniform(-wideY,wideY,n).reshape(n,-1) #纵轴噪声
    x=t+noisyX #横轴实际值
    y=u+noisyY #纵轴实际值
    return t,u,x,y

t,u,x,y=generate_samples()
rbf=RBF(0.003,20001,4) #学习率
rbf.train(x,y)
pre=rbf.predict(t)
plt.plot(x,y,'+')
plt.plot(t,u)
plt.plot(t,pre)
plt.legend(['dot','real','pre'],loc='upper left')

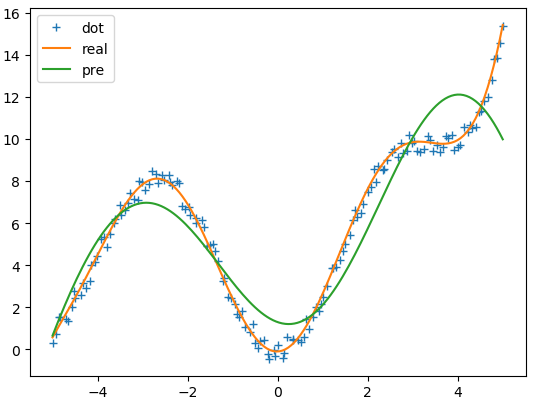自组织学习选取RBF中心

（2）有监督学习选取RBF中心

test_Supervised.py

import numpy as np
import matplotlib.pyplot as plt
from RBF_Supervised import RBF

#待逼近的函数
def fun(x):
    return x*x+2*x*np.sin(x)-np.exp(-x)/10

#生成样本
def generate_samples():
    n=150 #样本点个数
    wideX=0.03 #横轴噪声的宽度
    wideY=0.5 #纵轴噪声宽度
    t=np.linspace(-5,5,n).reshape(-1,1) #横轴理想值
    u=fun(t) #纵轴理想值
    noisyX=np.random.uniform(-wideX,wideX,n).reshape(n,-1) #横轴噪声
    noisyY=np.random.uniform(-wideY,wideY,n).reshape(n,-1) #纵轴噪声
    x=t+noisyX #横轴实际值
    y=u+noisyY #纵轴实际值
    return t,u,x,y

t,u,x,y=generate_samples()
rbf=RBF(0.003,20001,4) #学习率
rbf.train(x,y)
pre=rbf.predict(t)
plt.plot(x,y,'+')
plt.plot(t,u)
plt.plot(t,pre)
plt.legend(['dot','real','pre'],loc='upper left')

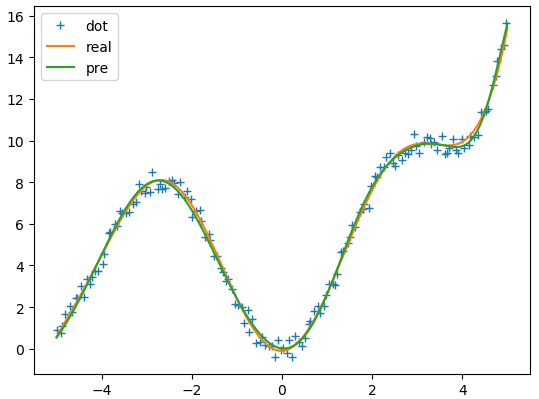有监督学习选取RBF中心

3.2 二元函数逼近

待逼近函数：

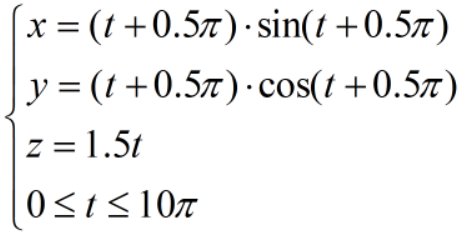
（1）自组织学习选取RBF中心

test_kmeans2.py

import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from RBF_kmeans import RBF

#待逼近的函数
def fun(t):
    x1=(t+0.5*np.pi)*np.sin(t+0.5*np.pi)
    x2=(t+0.5*np.pi)*np.cos(t+0.5*np.pi)
    y=1.5*t
    x=np.append(x1,x2,1)
    return x,y

#生成样本
def generate_samples():
    n=200 #样本点个数
    wideX=0.6 #水平方向噪声的宽度
    wideY=1 #纵轴噪声宽度
    t=np.linspace(0,10*np.pi,n).reshape(-1,1) #横轴理想值
    u,v=fun(t) #纵轴理想值
    noisyX=np.random.uniform(-wideX,wideX,u.shape).reshape(n,-1) #水平方向噪声
    noisyY=np.random.uniform(-wideY,wideY,n).reshape(n,-1) #纵轴噪声
    x=u+noisyX #横轴实际值
    y=v+noisyY #纵轴实际值
    return u,v,x,y

u,v,x,y=generate_samples()
rbf=RBF(0.02,20001,10) #学习率
rbf.train(x,y)
pre=rbf.predict(u)

ax=plt.figure().gca(projection='3d')
ax.plot(x[:,0],x[:,1],y[:,0],'+')
ax.plot(u[:,0],u[:,1],v[:,0])
ax.plot(u[:,0],u[:,1],pre[:,0])
plt.legend(['dot','real','pre'],loc='upper left')
plt.show()

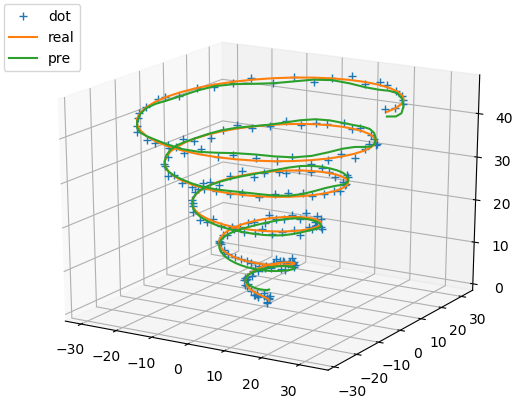自组织学习选取RBF中心

（2）有监督学习选取RBF中心

test_Supervised2.py

import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from RBF_Supervised import RBF

#待逼近的函数
def fun(t):
    x1=(t+0.5*np.pi)*np.sin(t+0.5*np.pi)
    x2=(t+0.5*np.pi)*np.cos(t+0.5*np.pi)
    y=1.5*t
    x=np.append(x1,x2,1)
    return x,y

#生成样本
def generate_samples():
    n=200 #样本点个数
    wideX=0.6 #水平方向噪声的宽度
    wideY=1 #纵轴噪声宽度
    t=np.linspace(0,10*np.pi,n).reshape(-1,1) #横轴理想值
    u,v=fun(t) #纵轴理想值
    noisyX=np.random.uniform(-wideX,wideX,u.shape).reshape(n,-1) #水平方向噪声
    noisyY=np.random.uniform(-wideY,wideY,n).reshape(n,-1) #纵轴噪声
    x=u+noisyX #横轴实际值
    y=v+noisyY #纵轴实际值
    return u,v,x,y

u,v,x,y=generate_samples()
rbf=RBF(0.02,20001,10) #学习率
rbf.train(x,y)
pre=rbf.predict(u)

ax=plt.figure().gca(projection='3d')
ax.plot(x[:,0],x[:,1],y[:,0],'+')
ax.plot(u[:,0],u[:,1],v[:,0])
ax.plot(u[:,0],u[:,1],pre[:,0])
plt.legend(['dot','real','pre'],loc='upper left')
plt.show()

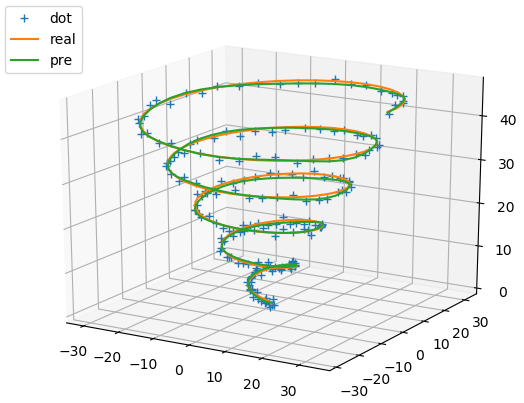有监督学习选取RBF中心

通过实验可以看到：无论是一元函数逼近还是二元函数逼近，在隐藏层神经元个数、学习率、学习步数相同的情况下，有监督学习法都比自组织学习法效果好。

​ 声明：本文转自基于tensorflow的RBF神经网络案例