HanLP — HMM隐马尔可夫模型 -- 维特比(Viterbi)算法 --示例代码 - Java

Viterbi 维特比算法解决的是篱笆型的图的最短路径问题，图的节点按列组织，每列的节点数量可以不一样，每一列的节点只能和相邻列的节点相连，不能跨列相连，节点之间有着不同的距离，距离的值就不在

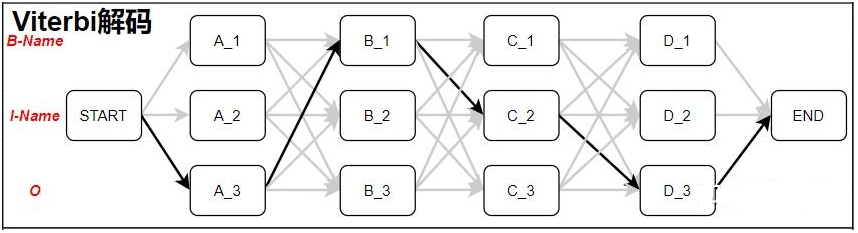
题目背景

从前有个村儿，村里的人的身体情况只有两种可能：健康、发烧。

假设这个村儿的人没有体温计或者百度这种神奇东西，他唯一判断他身体情况的途径就是到村头我的偶像金正月的小诊所询问。月儿通过询问村民的感觉，判断她的病情，再假设村民只会回答正常、头晕或冷。

有一天村里奥巴驴就去月儿那去询问了。

• 第一天她告诉月儿她感觉正常。
• 第二天她告诉月儿感觉有点冷。
• 第三天她告诉月儿感觉有点头晕。
  
  那么问题来了，月儿如何根据阿驴的描述的情况，推断出这三天中阿驴的一个身体状态呢?

已知情况

隐含的身体状态 = {健康,发烧}

可观察的感觉状态 = {正常,冷,头晕}

月儿预判的阿驴身体状态的概率分布（初始状态矩阵） = {健康:0.6,发烧:0.4}

月儿认为的阿驴身体健康状态的转换概率分布（转移矩阵） =

{
健康->健康： 0.7 ,
健康->发烧： 0.3 ,
发烧->健康：0.4 ,
发烧->发烧： 0.6
}

月儿认为的在相应健康状况条件下，阿驴的感觉的概率分布(发射矩阵) =

{
健康，正常：0.5 ，冷 ：0.4 ，头晕： 0.1 ；
发烧，正常：0.1 ，冷 ：0.3 ，头晕： 0.6
}

由上面我们可以发现，HMM的三要素都齐备了，下面就是解决问题了。

阿驴连续三天的身体感觉依次是： 正常、冷、头晕 。

过程：

第一天的时候，对每一个状态（健康或者发烧），分别求出第一天身体感觉正常的概率：P(第一天健康) = P(正常|健康)P(健康|初始情况) = 0.5 * 0.6 = 0.3 P(第一天发烧) = P(正常|发烧)P(发烧|初始情况) = 0.1 * 0.4 = 0.04

第二天的时候，对每个状态，分别求在第一天状态为健康或者发烧情况下观察到冷的最大概率。在维特比算法中，我们先要求得路径的单个路径的最大概率，然后再乘上观测概率。P(第二天健康) = max{0.30.7, 0.040.4}0.4=0.30.70.4=0.084 此时我们需要记录概率最大的路径的前一个状态，即0.084路径的前一个状态，我们在小本本上记下，第一天健康。 P(第二天发烧)=max{0.30.3, 0.040.6}0.3=0.027, 同样的在0.027这个路径上，第一天也是健康的。

第三天的时候，跟第二天一样。P(第三天健康)=max{0.0840.7, 0.0270.4}0.1=0.00588，在这条路径上，第二天是健康的。P(第三天发烧)=max{0.0840.3, 0.0270.6}0.6=0.01512,在这条路径上，第二天是健康的。

最后一天的状态概率分布即为最优路径的概率，即P(最优)=0.01512，这样我们可以得到最优路径的终点，是发烧

由最优路径开始回溯。请看我们的小本本，在求得第三天发烧概率的时候，我们的小本本上面写的是第二天健康，好了，第二天就应该是健康的状态，然后在第二天健康的情况下，我们记录的第一天是健康的。这样，我们的状态序列逆推出来了。即为：健康，健康，发烧

简略的画个图吧：



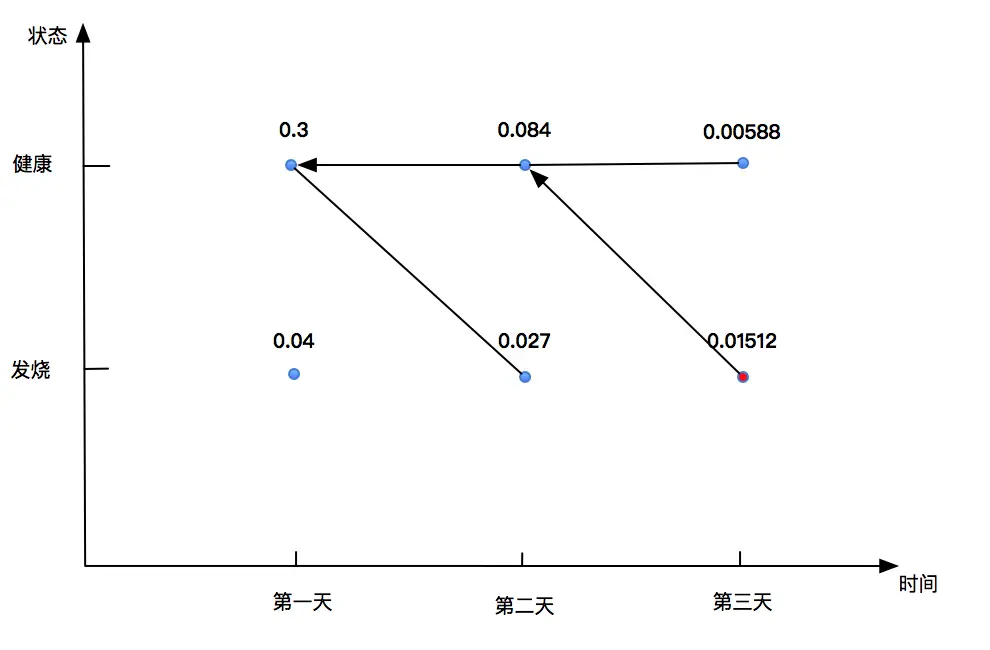
这儿的箭头指向就是一个回溯查询小本本的过程，我们在编写算法的时候，其实也得注意，每一个概率最大的单条路径上都要把前一个状态记录下来。

代码

Viterbi

package com.vipsoft.viterbi;
/**
 * 维特比算法
 * @author hankcs
 */
public class Viterbi
{
    /**
     * 求解HMM模型
     * @param obs 观测序列
     * @param states 隐状态
     * @param start_p 初始概率（隐状态）
     * @param trans_p 转移概率（隐状态）
     * @param emit_p 发射概率 （隐状态表现为显状态的概率）
     * @return 最可能的序列
     */
    public static int[] compute(int[] obs, int[] states, double[] start_p, double[][] trans_p, double[][] emit_p)
    {
        double[][] V = new double[obs.length][states.length];
        int[][] path = new int[states.length][obs.length];
        for (int y : states)
        {
            V[0][y] = start_p[y] * emit_p[y][obs[0]];
            path[y][0] = y;
        }
        for (int t = 1; t < obs.length; ++t)
        {
            int[][] newpath = new int[states.length][obs.length];
            for (int y : states)
            {
                double prob = -1;
                int state;
                for (int y0 : states)
                {
                    double nprob = V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]];
                    if (nprob > prob)
                    {
                        prob = nprob;
                        state = y0;
                        // 记录最大概率
                        V[t][y] = prob;
                        // 记录路径
                        System.arraycopy(path[state], 0, newpath[y], 0, t);
                        newpath[y][t] = y;
                    }
                }
            }
            path = newpath;
        }
        double prob = -1;
        int state = 0;
        for (int y : states)
        {
            if (V[obs.length - 1][y] > prob)
            {
                prob = V[obs.length - 1][y];
                state = y;
            }
        }
        return path[state];
    }
}

DoctorExample

package com.vipsoft.viterbi;
import static com.vipsoft.viterbi.DoctorExample.Feel.cold;
import static com.vipsoft.viterbi.DoctorExample.Feel.dizzy;
import static com.vipsoft.viterbi.DoctorExample.Feel.normal;
import static com.vipsoft.viterbi.DoctorExample.Status.Fever;
import static com.vipsoft.viterbi.DoctorExample.Status.Healthy;
public class DoctorExample
{
    enum Status
    {
        /**
         * 健康
         */
        Healthy,
        /**
         * 发热
         */
        Fever,
    }
    enum Feel
    {
        /**
         *  正常
         */
        normal,
        /**
         * 冷
         */
        cold,
        /**
         * 头晕
         */
        dizzy,
    }
    static int[] states = new int[]{Healthy.ordinal(), Fever.ordinal()};
    /**
     * 初始矩阵
     * { 健康：0.6 , 发烧： 0.4 }
     */
    static double[] start_probability = new double[]{0.6, 0.4};
    /**
     * 转移矩阵
     * {
     *  健康->健康：0.7 ,
     *  健康->发烧：0.3 ,
     *  发烧->健康：0.4 ,
     *  发烧->发烧：0.6
     * }
     */
    static double[][] transititon_probability = new double[][]{
            {0.7, 0.3},
            {0.4, 0.6},
    };
    /**
     * 发射矩阵
     * {
     *   健康，正常：0.5 ，冷 ：0.4 ，头晕： 0.1 ；
     *   发烧，正常：0.1 ，冷 ：0.3 ，头晕： 0.6
     * }
     */
    static double[][] emission_probability = new double[][]{
            {0.5, 0.4, 0.1},
            {0.1, 0.3, 0.6},
    };
    public static void main(String[] args)
    {
        // 连续三天的身体感觉依次是： 正常、冷、头晕，推算出这三天的身体状态
        int[] observations = new int[]{normal.ordinal(), cold.ordinal(), dizzy.ordinal()};
        int[] result = Viterbi.compute(observations, states, start_probability, transititon_probability, emission_probability);
        for (int r : result)
        {
            System.out.print(Status.values()[r] + " ");
        }
        System.out.println();
    }
}

源码：https://gitee.com/VipSoft/VipBoot/tree/develop/vipsoft-viterbi/src/main/java/com/vipsoft/viterbi

引用：https://www.zhihu.com/question/20136144 里的问题回答，正好是 HanLP 的Demo示例