力扣5(java)-最长回文串（中等）

题目：

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。
示例 2：

输入：s = "cbbd"
输出："bb"

提示：

1 <= s.length <= 1000
s 仅由数字和英文字母组成

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/longest-palindromic-substring
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路：

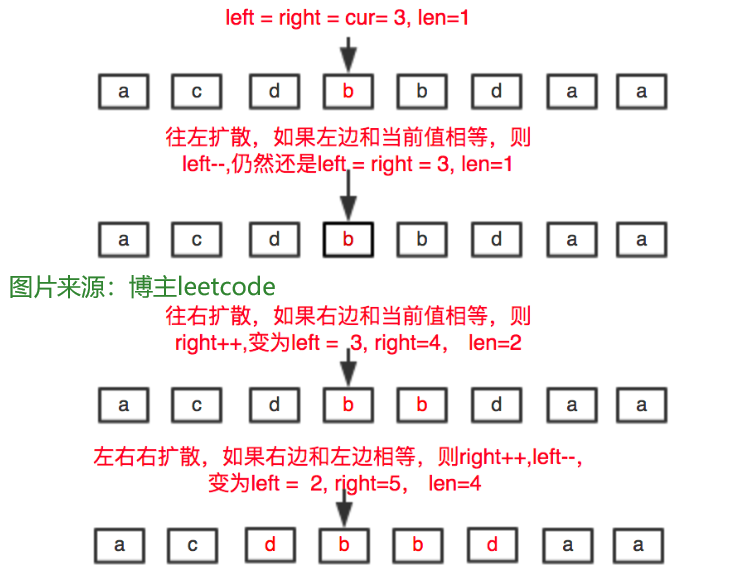
中心扩散法

从每一个位置向两边扩散，记录最大回文串的长度和起始位置

• 首先向左边扩散，如果左边的字符与当前字符相同，则 left--，回文串长度len++,否则退出当前左边扩散；
• 然后向右边扩散，如果右边的字符与当前字符相同，则 right++，回文串长度len++,否则退出当前右边扩散；
• 最后向左右两边扩散，如果左边和右边的字符相同，则left--,right++,回文串长度加2，否则退出当前扩散。

更新回文串的最大长度和起始位置，将当前回文串的长度置为1，扩散结束后，返回最大回文串--

s.substring(maxstart + 1, maxstart + 1 + maxlen)：由于之前遍历结束后已经将left的值更新过才会不满足While条件，这时left已经在起始位置的前一个位置，故这里需要加1，结束位置也同样需要加1，并且这里的substring取值是左开右闭区间。

例如：

直观一点：

代码：

 1 class Solution {
 2     public String longestPalindrome(String s) {
 3         //定义回文长度是初始值
 4         int len = 1;
 5         int n = s.length();
 6         int left = 0,right = 0;
 7         //记录最长回文的起始位置和最大长度
 8         int maxlen = 0, maxstart = 0;
 9         for(int i = 0; i < n; i++){
10             left = i - 1;
11             right = i + 1;
12             //向左扩展
13             while(left >= 0 && s.charAt(left) == s.charAt(i)){
14                 left--;
15                 len++;
16             }
17             //向右扩展
18             while(right <= n-1 && s.charAt(right) == s.charAt(i)){
19                 right++;
20                 len++;
21             }
22             //向左右两边扩展
23             while(left >= 0 && right <= n-1 && s.charAt(left) == s.charAt(right)){
24                 right++;
25                 left--;
26                 len += 2;
27             }
28             //如果当前会问长度大于最大长度，则更新最大长度和起始位置
29             if(len > maxlen){
30                 maxlen = len;
31                 maxstart = left;
32             }
33             //将当前长度重置
34             len = 1;
35         }
36         return s.substring(maxstart + 1, maxstart + 1 + maxlen);
37     }
38 }