【强化学习】Markov Decision processes【二】

Markov Decision processes
- Markov Process
- Markov reward process

Markov Decision processes

马尔可夫决策过程，里面有几个术语state,episode,history,value,gain。在后续的学习中，也会有这些术语。

Markov Decision processes 广泛应用于计算机科学和其他工程领域。所以很好的理解它。我们可以分解如下:

Markov Process(MP).(别名：Markov chain)
Markov reward Processes.这里扩展了一个Reward值。
Mark Decision Processes(MDPs).

Markov Process

这个过程，你只能观察他们的状态。这些状态它们本身有自己的动态变化规则。不为你的意志为转移，我们就只能观察他们。

这些状态的集合，有个名字叫做state space。然后我们随着时间的推移可以获得一个状态链子。（这就是为什么它的别名叫做Markov chain）。举例：中国的南昌市，有晴天和雨天。那么，5天的工作日可能就是[晴天，雨天，雨天，晴天，晴天]。我们观察到就是这个状态链子,我们也称它们为history。

马可夫性质（英语：Markov property），当一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态。啥意思呢？就是今天是晴天，那么明天是晴天还是雨天？依赖于【今天晴天】转为为【明天晴天】和【明天雨天】的概率是多少？

这里我们就可以用一个transition matrix【转移矩阵】来代表上述状态的转移概率。如下表:

	晴天	雨天
晴天	0.8	0.2
雨天	0.1	0.9

这是一个方形矩阵，有i行和j列。那么它的数值表示是state i转移到state j的概率。

什么意思呢？就是如上表，第一行的【晴天】，转移成【明天晴天】的概率是80%，转移成【明天雨天】的概率是20%。第二行的【雨天】，转移成【明天晴天】的概率是10%，转移成【明天雨天】的概率是90%。

所以Markov Process的定义：

有一个状态的集合,states(S)
有一个转移矩阵,transition matrix(T),代表是转移的概率。

MP的可视化表示:

可以看出，我们只能观察上述的变化。没有办法影响他们。【一切都是根据概率随机的变化】

我们给出一个更复杂的例子，来观察他们的状态变化。我们的state space如下:

家：家里休息
科学研究：去实验室做科学研究
喝咖啡:在实验室喝一杯咖啡
聊天：和同事针对某个问题讨论，当然，也可能聊闲天。

如下图:

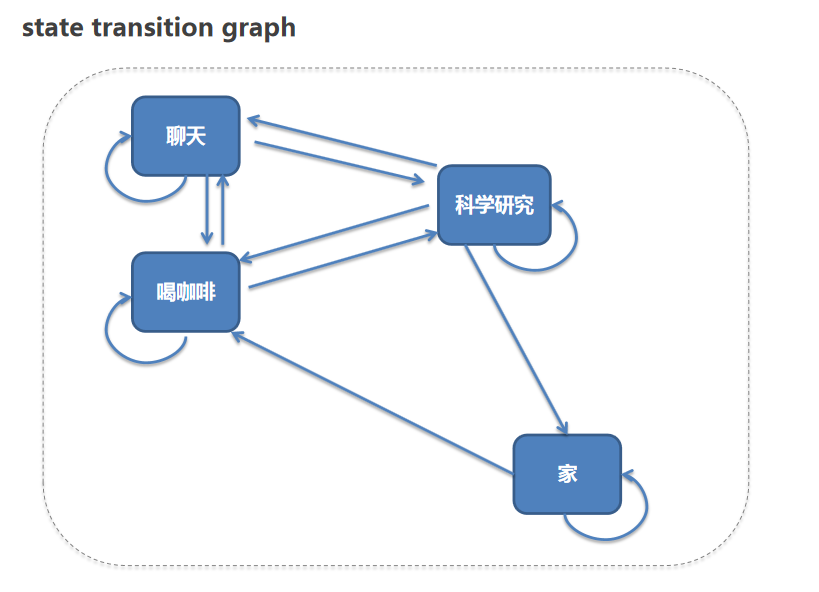
我们假定一些规则。例如:你可能从家里去实验室做科研研究，或者去实验室先去喝一杯咖啡再工作。例如，工作遇到问题会去找同事交流沟通等等。那么这些状态变化的概率【概率也是我们自己人为设定的】，我们做一个矩阵。

	家	喝咖啡	聊天	科学研究
家	60%	40%	0%	0%
喝咖啡	0%	10%	70%	20%
聊天	0%	20%	50%	30%
科学研究	20%	20%	10%	50%

加上状态变化的概率图，如下:

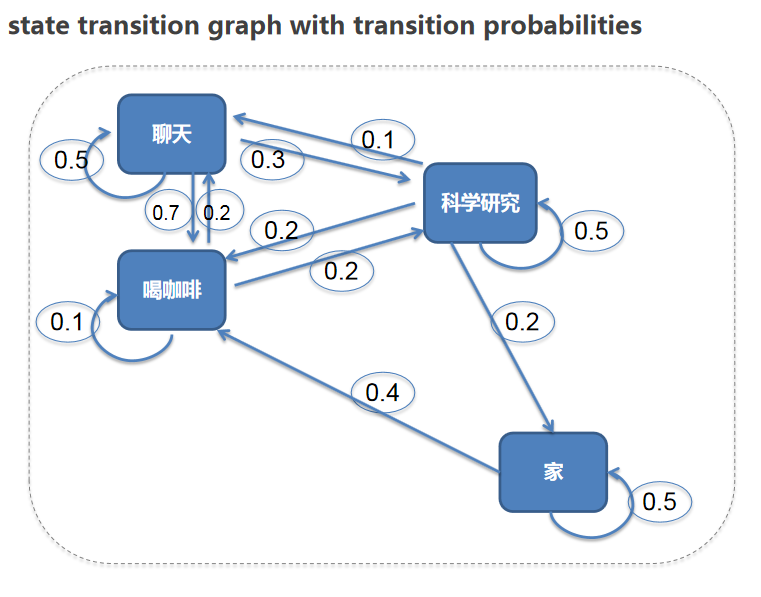
这个如果想象成一个真实的时间，每天都会发生不同的经历片段(episodes)：

家->喝咖啡->聊天->科学研究->家
家->喝咖啡->聊天->聊天->科学研究->聊天—>喝咖啡->科学研究->家
家->喝咖啡->科学研究->家

我们会发现，每天可能呈现的片段都是不一样的。但是如果你采样的数据足够多，它们的概率分布会是相同的。例如:硬币丢正反。可能10盘里面，70%是正面，30%是反面。但是如果丢10万盘，那么他们的正反面就会无限接近50%的概率。这种概率统计它的魅力也就在于此。

对于RL来说，这种不加手段的自我变化。对于我们来说，是没有很大意义的。为了让他们的变化，接近我们的目标。我们就必须加入reward。来强化它们的行为。那么它就叫做Markov reward process

Markov reward process

可以看到上述图中状态的变化是根据我们设定的概率进行变化的。我们现在给它加个scalar number。

例如:从【家】到【喝咖啡】这个状态变化概率相当于从state i到state j这个状态。我们给与奖励值可以正面的，也可以是负面的。是一个数值。这样就会让他们变化效果更符合我们预期。

除了reward还有一个参数，discount facter γ(gamma)。

上面讨论过，通过观察，我们会获得一个状态链子如:【家->喝咖啡->聊天->科学研究->家】，由于我们给了一个额外的奖励值。所以，对于每一个的episode。我们都可以算出一个这个时间t我们获取的奖励值数量。公式如下:

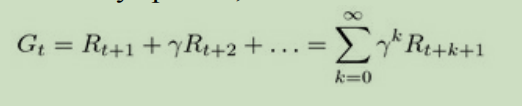
我们把上述的公式，在多扩展几项如下:

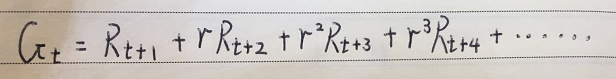
可以看到，离我们距离越远的时间，我们的γ相乘数越高。例如：0.9的50次方。就是0.005.这个公式，也是为了表现agent的前瞻性。同时，γ的取值在0~1.

这里，由于每一个状态链子都可能不一样，那么获得奖励值数量也会不同。然而，我们可以用数学期望。通过计算一个状态链子的平均值。这个叫做:value of state公式如下:

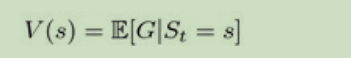
由于理论是空洞难懂的。我们继续举上面那个例子。我们对每一个状态变化设一个奖励值:

家->家：得 1 分
家->喝咖啡 : 得1分
科学研究 ->科学研究 : 得 5 分
科学研究 ->聊天: 得 -3 分
聊天 -> 科学研究: 得 2 分
科学研究 ->喝咖啡 : 得 1 分
喝咖啡 ->科学研究 : 得 3 分
喝咖啡 ->喝咖啡 : 得 1 分
喝咖啡 ->聊天 : 得 2 分
聊天 ->喝咖啡 : 得 1 分
聊天 ->聊天 : 得 -1 分

未完待续