【HDU5955】Guessing the Dice Roll/马尔科夫

先从阿里机器学习算法岗网络笔试题说起：甲乙两人进行一个猜硬币的游戏。每个人有一个目标序列，由裁判来抛硬币。谁先得到裁判抛出的一串连续结果，谁赢。

甲的目标序列是正正正，乙的目标序列是反正正。那么如果裁判抛出了正正反正反正正....抛到第7个结果时乙胜，因为最后三个序列是“反正正”，而前面不存在甲的“正正正”序列。

问：甲的目标序列是？？？？，乙的目标序列是？？？？，求两人各自获胜的概率。

先说例子，正正正，反正正的概率。显然是1/8和7/8.  甲获胜的情况只有一种，就是三个连续的正，P = 1/8。为什么呢？因为，一旦裁判抛出一个“反”，结果就已经确定是乙胜了。所以甲要想获胜，只能从开头就是连着三个正。

那么对于一般题怎么做呢？

AC自动机 + 高斯消元。

你可以理解成 有限状态自动机+解方程。

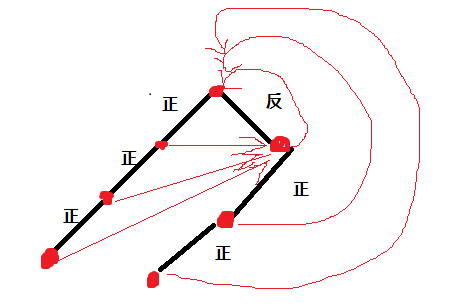
(不好意思  这个图有误，所有曲线指的不应该是根节点，而应该是根节点读入"反"后的右节点)

根节点是开始，每抛出一个硬币走一条边。谁先走到最底下的点就胜。

到底部的获胜概率就是从开始局面到底部的期望次数。(到所有终点的期望和是1，等价于所有人的获胜概率和是1)

这么转换后就能做了。每个结点的期望 = 它前驱结点的期望 的 加权平均值。

如果只有一条边出去，那么它的下一个结点的期望显然就等于它的期望。

自环也算进去，加权算。

那么就能对每个结点列方程，n元一次方程。常数项在哪里？

在根节点前虚拟一个结点，指向根结点。虚拟结点的期望是1。

然后就能高斯消元做了！

以上的过程其实是一个 马尔科夫 过程。

我们解决了自动机到终点的概率（获胜概率，也就是到终点的期望次数），我们类似可以解决自动机走到终点的期望步数。也就是裁判期望抛多少回硬币游戏能够结束？

同样是列方程。

xi表示到i结点需要走的期望步数， xi = 1+∑ (pj*xj), (xj 是xi 的前驱结点, pj是xj结点走到到xi结点的概率)？？？

xi表示从i结点走到终点的期望步数， xi = 1+∑ (pj*xj), (xj 是xi 的后继结点, pj是xj结点走到到xi结点的概率)

以上。

扩展

如果你和一个人玩游戏，是否存在一种情况，无论对方的序列是什么序列，你都能够构造出一个 等长 的序列，使你的获胜概率比对方大？

答案是：当序列长度 > 2时，你总能使自己获胜概率更大。

详见 matrix67

现场赛的题是投骰子，谁先投出自己的序列谁胜。求各自获胜概率。

正解：ac自动机+高斯消元。

有一个做n遍消元的解法：对每个人的目标点消元。具体就是设xi为i结点到目标点的概率，dp算出根结点的值就是从根节点到目标点的概率。做n次即可。

还有一种有误差的解法。矩阵快速幂。矩阵的n次幂表示从根节点走n步到各个点的概率。n足够大时，就能近似表示出到各个点的概率。可惜，精度还是不够，误差比较大。。。。

还是要贴一下AC代码的。

 #include <bits/stdc++.h>
 #define gg puts("gg");
 using namespace std;
 const double eps = 1e-;
 const int N  = ;
 int id(int c){
     return c-;
 }
 struct Tire{
     int nex[N][], fail[N], end[N];
     int root, L;
     int newnode(){
         memset(nex[L], -, sizeof(nex[L]));
         end[L] = ;
         return L++;
     }
     void init(){
         L = ;
         root = newnode();
     }
     void insert(int* s, int l, int k){
         int now = root;
         for(int i = ; i < l; i++){
             int p = id(s[i]);
             if(nex[now][p] == -)
                 nex[now][p] = newnode();
             now = nex[now][p];
         }
         end[now] = k;
     }
     void build(){
         queue<int> Q;
         fail[root] = root;
         for(int i = ; i < ; i++){
             int& u = nex[root][i];
             if(u == -)
                 u = root;
             else{
                 fail[u] = root;
                 Q.push(u);
             }
         }
         while(!Q.empty()){
             int now = Q.front();
             Q.pop();
             for(int i = ; i < ; i++){
                 int& u = nex[now][i];
                 if(u == -)
                     u = nex[ fail[now] ][i];
                 else{
                     fail[u] = nex[ fail[now] ][i];
                     end[u] |= end[ fail[u] ];
                     //last[u] = end[ fail[u] ]? fail[u] : last[ fail[u] ];
                     Q.push(u);
                 }
             }
         }
     }
 };
 Tire ac;

 double a[][], x[], ans[];
 int equ, var;
 int Gauss(){
     int i,j,k,col,max_r;
     for(k = , col = ; k < equ&&col < var; k++, col++){
         max_r = k;
         for(i = k+; i < equ; i++)
             if(fabs(a[i][col]) > fabs(a[max_r][col]))
                 max_r = i;
         if(fabs(a[max_r][col]) < eps) return ;
         if(k != max_r){
             for(j = col; j < var; j++)
                 swap(a[k][j], a[max_r][j]);
             swap(x[k], x[max_r]);
         }
         x[k] /= a[k][col];
         for(j = col+; j < var; j++) a[k][j] /= a[k][col];
         a[k][col] = ;
         for(i = ; i < equ; i++)
         if(i != k){
             x[i] -= x[k]*a[i][k];
             for(j = col+; j < var; j++) a[i][j] -= a[k][j]*a[i][col];
             a[i][col] = ;
         }
     }
     return ;
 }

 int s[];
 int main(){
     int n, l, t, ca = ; scanf("%d", &t);
     while(t--){
         ac.init();
         scanf("%d%d", &n, &l);
         for(int i = ; i <= n; i++){
             for(int j = ; j < l; j++)
                 scanf("%d", s+j);
             ac.insert(s, l, i);
         }
         ac.build();

         memset(a, , sizeof(a));
         memset(x, , sizeof(x));
         equ = ac.L, var = ac.L;
         for(int i = ; i < ac.L; i++)
             a[i][i] = -;
         x[] = -;
         for(int i = ; i < ac.L; i++){
             if(!ac.end[i])
                 for(int j = ; j < ; j++){
                     int to = ac.nex[i][j];
                     a[to][i] += 1.0/;
                 }
         }

         Gauss();

         for(int i = ; i < ac.L; i++)
             if(ac.end[i]) ans[ ac.end[i] ] = x[i];
         for(int i = ; i <= n; i++)
             printf("%.6f%c", ans[i], " \n"[i == n]);
     }
     return ;
 }