关联分析---Apriori

关联分析是一种在大规模数据集中寻找有趣关系的任务，这些关系有两种形式：频繁项集和关联规则。频繁项集是经常出现在一起的物品的集合，关联规则暗示两种物品之间可能存在的很强的关系。

如何寻找数据集中的频繁或关联关系呢？主要是通过支持度和可信度。

一个项集的支持度被定义为数据集中包含该项集的记录所占的比例。

可信度是针对关联规则来定义的，比如规则A->B的可信度为：支持度{A,B} / 支持度{A}

支持度和可信度是用来量化关联分析是否成功的方法。

Apriori原理：

要计算某个项集在数据集的支持度，需要大量的计算。一个有N个数据的集合共有2^N-1种项集的组合，即N=100的数据集可能有2¹⁰⁰-1中项集的组合，对于普通的计算机而言，需要很长的时间才能完成运算。

为了降低所需的计算时间，通常采用采用Apriori原理，来减少可能感兴趣的项集。

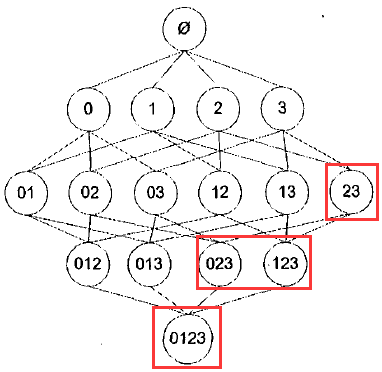
Apriori在拉丁语中指“来自以前”， Apriori原理：如果某个项集是频繁的，那么它的所有子集也是频繁的；如果一个项集是非频繁集，那么它的所有超集也是非频繁的。

比如，一旦计算出{2,3}的支持度，知道它是非频繁的项集，则可推出{1,2,3}，{0,2,3}等包含{2,3}的项集也是非频繁的，就不需要再进行计算支持度了。

使用该原理就可以避免项集数据的指数增长，从而在合理的时间内计算出频繁项集。

使用Apriori算法来发现频繁集：

def loadDataSet():
    return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]

def createC1(dataSet):
    C1 = []
    for transaction in dataSet:
        for item in transaction:
            if not [item] in C1:
                C1.append([item])

    C1.sort()
    return map(frozenset, C1)#use frozen set so we
                            #can use it as a key in a dict    

def scanD(D, Ck, minSupport):
    ssCnt = {}
    for tid in D:
        for can in Ck:
            if can.issubset(tid):
                if not ssCnt.has_key(can): ssCnt[can]=1
                else: ssCnt[can] += 1
    numItems = float(len(D))
    retList = []
    supportData = {}
    for key in ssCnt:
        support = ssCnt[key]/numItems
        if support >= minSupport:
            retList.insert(0,key)
        supportData[key] = support
    return retList, supportData

def aprioriGen(Lk, k): #creates Ck
    retList = []
    lenLk = len(Lk)
    for i in range(lenLk):
        for j in range(i+1, lenLk):
            L1 = list(Lk[i])[:k-2]; L2 = list(Lk[j])[:k-2]
            L1.sort(); L2.sort()
            if L1==L2: #if first k-2 elements are equal
                retList.append(Lk[i] | Lk[j]) #set union
    return retList

def apriori(dataSet, minSupport = 0.5):
    C1 = createC1(dataSet)
    D = map(set, dataSet)
    L1, supportData = scanD(D, C1, minSupport)
    L = [L1]
    k = 2
    while (len(L[k-2]) > 0):
        Ck = aprioriGen(L[k-2], k)
        Lk, supK = scanD(D, Ck, minSupport)#scan DB to get Lk
        supportData.update(supK)
        L.append(Lk)
        k += 1
    return L, supportData