[BZOJ1718]:[Usaco2006 Jan] Redundant Paths 分离的路径（塔尖）

题目传送门

---

题目描述

　　为了从F个草场中的一个走到另一个，贝茜和她的同伴们有时不得不路过一些她们讨厌的可怕的树．奶牛们已经厌倦了被迫走某一条路，所以她们想建一些新路，使每一对草场之间都会至少有两条相互分离的路径，这样她们就有多一些选择。
　　每对草场之间已经有至少一条路径．给出所有R条双向路的描述，每条路连接了两个不同的草场，请计算最少的新建道路的数量, 路径由若干道路首尾相连而成．两条路径相互分离，是指两条路径没有一条重合的道路．但是，两条分离的路径上可以有一些相同的草场． 对于同一对草场之间，可能已经有两条不同的道路，你也可以在它们之间再建一条道路，作为另一条不同的道路。

---

输入格式

第1行输入F和R，接下来R行，每行输入两个整数，表示两个草场，它们之间有一条道路。

---

输出格式

最少的需要新建的道路数。

---

样例

样例输入：

7 7
1 2
2 3
3 4
2 5
4 5
5 6
5 7

样例输出：

2

---

数据范围与提示

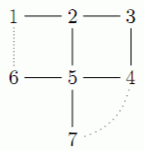
图中实线表示已有的道路，虚线表示新建的两条道路。

现在可以检验一些路径，比如：

草场1和草场2：1→2和1→6→5→2。

草场1和草场4：1→2→3→4和1→6→5→4。

草场3和草场7：3→4→7和3→2→5→7。

　　　　　　　　　事实上，每一对草场之间都连接了两条分离的路径。

1≤F≤5000，F-1≤R≤10000。

注意会有重边！！！

---

题解

看到这道题，马上想到了塔尖，缩e-DCC。

然后答案即为得到的$\frac{这棵树上的叶子节点的个数+1}{2}$，利用性质，连边为1的点即为叶子节点，统计答案即可。

代码细节较多，建议尝试自己根据自己的理解手打。

当然也有大神缩v-DCC，直接A掉。

还有这么一种解法，塔尖之后不用重新建图，而是直接判断在一条边两端的点low的值是否相同，如果不同那么就让度数+1。（他们的塔尖通过在一开始直接判断e.to是否等于father，如果相等直接continue）。

但是这样并不正确！！！

考虑这道题会有重边，所以如果low[x]≠low[y]，但是它们还可能属于一个强联通分量。

不过如果你使用了可以规避重边的方法，那么就没有问题。

综上所述，板子要理解，并能灵活运用！！！

---

代码时刻

e-DCC

#include<bits/stdc++.h>
using namespace std;
struct rec
{
	int from;
	int nxt;
	int to;
}e[200010],wzc[200010];
int head[5010],cnt=1;
int headw[5010],cntw=1;
int F,R;
int dfn[5010],low[5010],tot;
bool bridge[200010];
int c[5010],dcc;
int ans[5010];
int sum;
bool vis[5010];
void add(int x,int y)
{
	e[++cnt].nxt=head[x];
	e[cnt].from=x;
	e[cnt].to=y;
	head[x]=cnt;
}
void tarjan(int x,int in_edge)//判断桥
{
	dfn[x]=low[x]=++tot;
	for(int i=head[x];i;i=e[i].nxt)
	{
		if(!dfn[e[i].to])
		{
			tarjan(e[i].to,i);
			low[x]=min(low[x],low[e[i].to]);
			if(dfn[x]<low[e[i].to])
				bridge[i]=bridge[i^1]=1;
		}
		else if(i!=(in_edge^1))
			low[x]=min(low[x],dfn[e[i].to]);
	}
}
void dfs(int x)//求e-DCC
{
	c[x]=dcc;
	for(int i=head[x];i;i=e[i].nxt)
	{
		if(c[e[i].to]||bridge[i])continue;
		dfs(e[i].to);
	}
}
int main()
{
	scanf("%d%d",&F,&R);
	for(int i=1;i<=R;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		add(x,y);
		add(y,x);
	}
	for(int i=1;i<=F;i++)
	if(!dfn[i])tarjan(i,0);
	for(int i=1;i<=F;i++)
		if(!c[i])
		{
			++dcc;
			dfs(i);
		}
	for(int i=2;i<=cnt;i++)//开始计算答案
		if(c[e[i].from]!=c[e[i].to])ans[c[e[i].from]]++;
	for(int i=1;i<=dcc;i++)
		if(ans[i]==1)sum++;
	printf("%d",(sum+1)/2);
	return 0;
}

v-DCC

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
int const maxn=5010;
struct node{int st,to,nxt;}l[4*maxn];
vector<int>v[maxn];
int n,m,head[maxn],tot,num,in[maxn*2],ans;
int dfn[maxn],low[maxn],stack[maxn],bl[maxn*2],id[maxn*2],cut[maxn*2],top,now,cnt,rt;
void add1(int x,int y)
{
	l[++tot].to=y;
	l[tot].st=x;
	l[tot].nxt=head[x];
	head[x]=tot;
}
void tarjan(int x)//割点
{
	dfn[x]=low[x]=++now,stack[++top]=x;
	if(x==rt&&head[x]==0)
	{
		v[++cnt].push_back(x);
		bl[x]=cnt;
		return ;
	}
	int flag=0;
	for(int i=head[x];i;i=l[i].nxt)
	{
		int y=l[i].to;
		if(!dfn[y])
		{
			tarjan(y);
			low[x]=min(low[x],low[y]);
			if(low[y]>=dfn[x])
			{
				flag++;
				if(x!=rt||flag>1) cut[x]=1;
				cnt++;int z;
				do{
					z=stack[top--];
					v[cnt].push_back(z);
					bl[z]=cnt;
				}while(y!=z);
				v[cnt].push_back(x);
			}
		}
		else low[x]=min(low[x],dfn[y]);
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1,x,y;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		add1(x,y),add1(y,x);
	}
	for(int i=1;i<=n;i++) if(!dfn[i]) rt=i,tarjan(i);
	num=cnt;
	for(int i=1;i<=n;i++) if(cut[i]) id[i]=++num;
	for(int i=1;i<=cnt;i++)
		for(int j=0;j<v[i].size();j++)
			if(cut[v[i][j]]) in[i]++;
	for(int i=1;i<=cnt;i++) if(in[i]==1) ans++;
	printf("%d",(ans+1)/2);
	return 0;
}

---

rp++