TensorFlow学习笔记5-概率与信息论

本笔记内容为“概率与信息论的基础知识”。内容主要参考《Deep Learning》中文版。

$X$表示训练集的设计矩阵，其大小为m行n列，m表示训练集的大小(size)，n表示特征的个数；
$W$表示权重矩阵，其大小是n行k列，n为输入特征的个数，k为输出(特征)的个数；
$\boldsymbol{y}$表示训练集对应标签，其大小为m行，m表示训练集的大小(size)；
$\boldsymbol{y’}$表示将测试向量$x$输入后得到的测试结果；

频率派概率：概率直接与事件发生的频率相联系。贝叶斯概率：概率与事件发生的确定性水平相联系。

概率分布：随机变量(或一簇随机变量)在每个取值的可能性大小。

离散型变量：$P(x=x_1)$，$x\sim P(x)$表示随机变量$x$服从的概率分布。
- 归一化：$\sum_ {x_ {i} \in X} P(x_ {i})=1$
- 多个随机变量的概率分布称为联合概率分布。即$P(x,y)$
连续型变量：概率密度函数(Probability density function, PDF) $p(x)$表示无穷小区域的概率为 $p(x)\delta x$。
边缘概率：
- 离散型：$P(x)=\sum_y P(x,y)$
- 连续型：$p(x)=\int p(x,y)dy$
条件概率：
$P(y=y_ 0|x=x_ 0)=\frac{P(y=y_ 0,x=x_ 0)}{P(x=x_ 0)}$
条件概率的链式法则：
$P(a,b,c)=P(a|b,c)P(b,c)P(c)$
\[p(\boldsymbol{x})=p(x_ {1})\prod^{n}_ {i=2}p(x_ {i}|x_ {1},...,x_ {i-1})\]
贝叶斯规则:
\[P(x|y)=\frac{P(x)P(y|x)}{P(y)}\]
变量的独立性：
- $p(x,y)=p(x)p(y)$，记为$x \bot y$
- 条件独立性：$p(x,y|z)=p(x|z)p(y|z)$，记为$x \bot y |z$
期望：
- 离散型：$E_{x \sim P}[f(x)]= \sum_x P(x)f(x)$
- 连续型：$E_ {x \sim p}[f(x)]=\int p(x)f(x)dx$
- 线性的：$E[af(x)+bg(x)]=aE[f(x)]+bE[g(x)]$
方差：$Var(f(x))=E[(f(x)-E(f(x)))^2]$
协方差：$Cov(f(x),g(y))=E[(f(x)-E(f(x)))(g(y)-E(g(y)))]$

相互独立的两个随机变量协方差一定为0。协方差为0的两个变量不一定独立。
协方差矩阵$Cov(x)_ {i,j} = Cov(x_ i, x_ j)$，其对角元是方差$Cov(x_ i, x_ i)=Var(x_i)$

几种分布

伯努利分布(二值分布)：
\[P(x=1)=\phi \]
\[P(x=0)= 1-\phi \]
高斯分布(正态分布)：
\[f(x)=\sqrt{\frac{1}{2 \pi \sigma ^2}} \exp({- \frac{(x-\mu)^2}{2\sigma ^2}})\]
其中$\mu$为期望，$\sigma ^2$为方差，$\beta = 1/\sigma^2$为精度。
标准正态分布为$\mu=0,\sigma =1$的正态分布。
多维正态分布：
\[\boldsymbol{N(x;\mu,\Sigma)=\sqrt{\frac{1}{2 \pi \det(\Sigma)}} \exp({- \frac{(x-\mu)^T \Sigma^{-1} (x-\mu)}{2}})}\]
其中$\boldsymbol{\mu}$为期望，向量形式，$\boldsymbol{\Sigma}$是分布的协方差矩阵。
指数分布：
\[p(x;\lambda)=\lambda \exp(-\lambda x), subject\ to\ x \geq 0\]
LapLace分布：
\[Laplace(x;\mu,\gamma)=\frac{1}{2\gamma} \exp(- \frac{|x-\mu|}{\gamma})\]
Dirac分布：
\[p(x)=\delta (x-\mu)\]
经验分布：
\[\hat{p}(x)=\frac{1}{m}\sum^m_ {i=1} \delta (x-x^{(i)})\]
混合分布：
\[ P(x)=\sum_ {i} P(c=i)P(x|c=i)\]
混合分布由一系列形如$P(x|c=i)$的组件分布组成。常见的高斯混合模型的组件$P(x|c=i)$是高斯分布。可用来拟合多峰函数。
高斯混合模型是概率密度的通用近似器。

常用的函数
logistic sigmoid函数：$\sigma(x)=\frac{1}{1+\exp (-x)}$
softplus函数：$\zeta(x) = \log (1+ \exp (x))$可用来产生正态分布的$\beta$和$\sigma$参数。
- $ \sigma (x)=\frac{ \exp (x)}{\exp(x)+\exp(0)}$
- $ \frac{d}{dx}\sigma (x)=\sigma (x)(1-\sigma (x))$
- $ 1-\sigma (x)=\sigma (-x)$
- $ \log \sigma (x)= -\zeta(-x)$
- $ \frac{d}{dx}\zeta(x)=\sigma(x)$
- $ \forall x \in (0,1),\sigma^{-1}(x)= \log (\frac{x}{1-x})$
- $ \forall x>0, \zeta^{-1}(x)=\log (\exp (x)-1)$
- $ \zeta(x)=\int^x_ {-\infty} \sigma(y)dy$
- $ \zeta (x)-\zeta (-x)=x$

确定函数关系的两个随机变量的概率分布函数

设$y=g(x)$，要保证$|p_ y (g(x))dy| = |p_ x(x)dx|$ ，可以得到
\[p_y(y) = p_ {x}(g^{-1}(y))|\frac{\partial{x}}{\partial y}|\]
或
\[p_x(x) = p_ {y}(g(x))|\frac{\partial{g(x)}}{\partial x}|\]
高维空间中，扩展为：
\[p_x(\boldsymbol{x}) = p_ {y}(g(\boldsymbol{x}))|\det(\frac{\partial{g(\boldsymbol{x})}}{\partial \boldsymbol{x}})|\]

信息论基础

事件$x=x_0$的自信息为$I(x)=-\log P(x)$。当底数为$e$时，信息量单位为奈特(nats)，底数为2时，单位为比特或香农。这里底数为$e$。
香农熵为\[H(x)=E_ {x \sim P}[I(x)]=-\sum_ {i} P(x_ {i})\log P(x_ {i})\]
对同一个随机变量的两种单独的概率分布$P(x)$和$Q(x)$，其差异用KL散度衡量：\[D_ {KL}(P||Q)=E_ {x \sim P}[\log \frac{P(x)}{Q(x)}]
=E_ {x \sim P}[\log P(x) - \log Q(x)]=\sum_ {i} P(x_ {i})(\log P(x_ {i})- \log Q(x_ {i}))\]
注意计算$D_ {KL}(P||Q)$还是$D_ {KL}(Q||P)$是不一样的，因为$D_ {KL}(P||Q) \neq D_ {KL}(Q||P)$
。KL散度是不对称的。
一般已经拿到了$p(x)$的分布，用$q(x)$去近似。可以选择最小化$D_ {KL}(P||Q)$或$D_ {KL}(Q||P)$。

在机器学习中，$P(x),Q(x)$分别为基于数据集的经验分布(已知的)与设计的模型概率分布(估计的)。
最大化似然就是最小化KL散度，由于$\sum_i P(x_i)logP(x_i)$与模型无关，故最小化KL散度就是最小化交叉熵。
交叉熵：
\[H(P,Q)=-E_ {x \sim P}[\log Q(x)]=-\sum_ {i} P(x_ {i})\log Q(x_ {i}) \tag{1}\]

综上：在机器学习中，最大似然估计，等价于最小化交叉熵。即：任何时候优化函数就是交叉熵，也就是对数似然组成的损失函数(即式$(1)$)。

结构化概率模型-分解联合概率分布的计算

若3个随机变量a,b,c满足：a影响b的取值，b影响c的取值，但a和c在给定b时是条件独立的($p(a,c|b)=p(a|b)p(c|b)$)，则：
\[p(a,b,c)=p(a)p(b|a)p(c|b)\]

有向图模型分解：$p(\boldsymbol{x})=\prod_ {i} p(x_i |Pa\ g(x_i))$，其中$Pa\ g(x_i)$为节点$x_i $的父节点。
无向图模型分解：图中任何两两节点之间有边连接的节点的集合称为团，每个团有一个因子$\phi^{(i)}(C^{(i)})$，这些因子是非负的。
整体的联合分布为$p(\boldsymbol{x})=\frac{1}{Z}\prod_ {i}\phi^{(i)}(C^{(i)})$，其中$Z$为归一化常数。

独立同分布与估计

通常我们有样本，却不知道其中的概率密度模型如何。设每次采样是独立同分布的。

测试集样本独立同分布很多时，中心极限定理：样本均值接近高斯分布。

统计中的量：

样本均值：m个样本的平均值$\bar{x}=\frac{\sum_ {i}x_ {i}}{m}$
样本方差：$\sigma ^2 = \frac{1}{m}\sum^m_ {i=1}(x_ {i}-\bar{x})^2$

概率论中的量：

数学期望：$E(f(x))=\sum_ {i}f(x_ {i})P(x_ {i})$或$E(f(x))=\int f(x)p(x)dx$
方差：$var [f(x)]=E[(f(x)-E[f(x)])^2]$

常用样本均值估计：

二值分布的独立同分布的模型的 $\theta$参数 ；无偏估计。
高斯分布的 $\mu$参数 。无偏估计。

常用样本方差估计：

高斯分布的 $\sigma ^2$参数 ，有偏估计。
用 $\frac{m}{m-1}\times$样本方差 去估计高斯分布的 $\sigma ^2$参数，无偏估计。
虽然有偏，但还是用样本方差估计高斯分布的 $\sigma ^2$参数较多(样本量较大时，近似无偏)。

估计量的偏差：$bias(\hat{\theta}_ {m})=E(\hat{\theta}_ {m})-\theta$

其中,$\hat{\theta}_ {m}$为你从m个样本数据中计算出来的估计量，$\theta$为你要估计的模型中的参数。

估计量的方差用公式$Var [\hat{\theta}_ {m}]=E[(\hat{\theta}_ {m}-E[\hat{\theta}_ {m}])^2]$计算。
估计量的标准差为：$\sigma = \sqrt{Var(\hat{\theta})}$

例如：样本均值的标准差为$SE(\bar{x})=\sqrt{Var(\bar{x})}=\frac{\sigma}{\sqrt{m}}$

那么优化时，选择优化估计量的偏差还是优化估计量的方差呢?

如果选择最优化偏差，则方差可能很大，更关注整体，是一种欠拟合(训练误差较大)；
如果选择最优化方差，则偏差可能很大，更关注细节，是一种过拟合(训练误差与测试误差差距较大)。
选择最优化 均方误差(Mean Squared Error) 可以获得一种均衡。
\[MSE=E[(\hat{\theta}_ {m}-\theta)]=bias(\hat{\theta})_ {m}^2 + Var(\hat{\theta}_ {m})\]

对均方误差的进一步解释

以回归任务为例：对测试样本$x$，令$y_ {D}$为$x$在数据集中的标记，$y$为$x$的真实模型中标记，$f(x;D)$为训练集$D$上的模型的预测输出。

方差

在一个训练集$D$上模型 $f$ 对测试样本 $x$的预测输出为 $y'=f(x;D)$, 那么学习算法 $f$ 对测试样本 $x$ 的 期望预测 为:

\[\bar{f}(x)=E_ {D}[f(x;D)]\]
上面的期望预测也就是针对不同数据集 $D$, $f$ 对 $x$ 的预测值取其均值, 也被叫做 均值预测.

使用样本数相同的不同训练集产生的方差为:

\[Var(x)=E_ {D}[(f(x;D)−\bar{f}(x))^2]\]

噪声

噪声为真实标记与数据集中的实际标记间的偏差:

\[ϵ^2=E_ {D}[(y_ {D}−y)^2]\]
为方便起见，设噪声期望为0，即$E_ {D}[y_ {D}-y]=0$

偏差

期望预测与真实标记的误差称为偏差(bias), 为了方便起见, 我们直接取偏差的平方:

\[bias^2(\bar{f}(x))=(\bar{f}(x)−y)^2\]

估计的评价：均方误差(Mean Squared Error)

参考周志华老师书里的 期望泛化误差：均方误差¹：

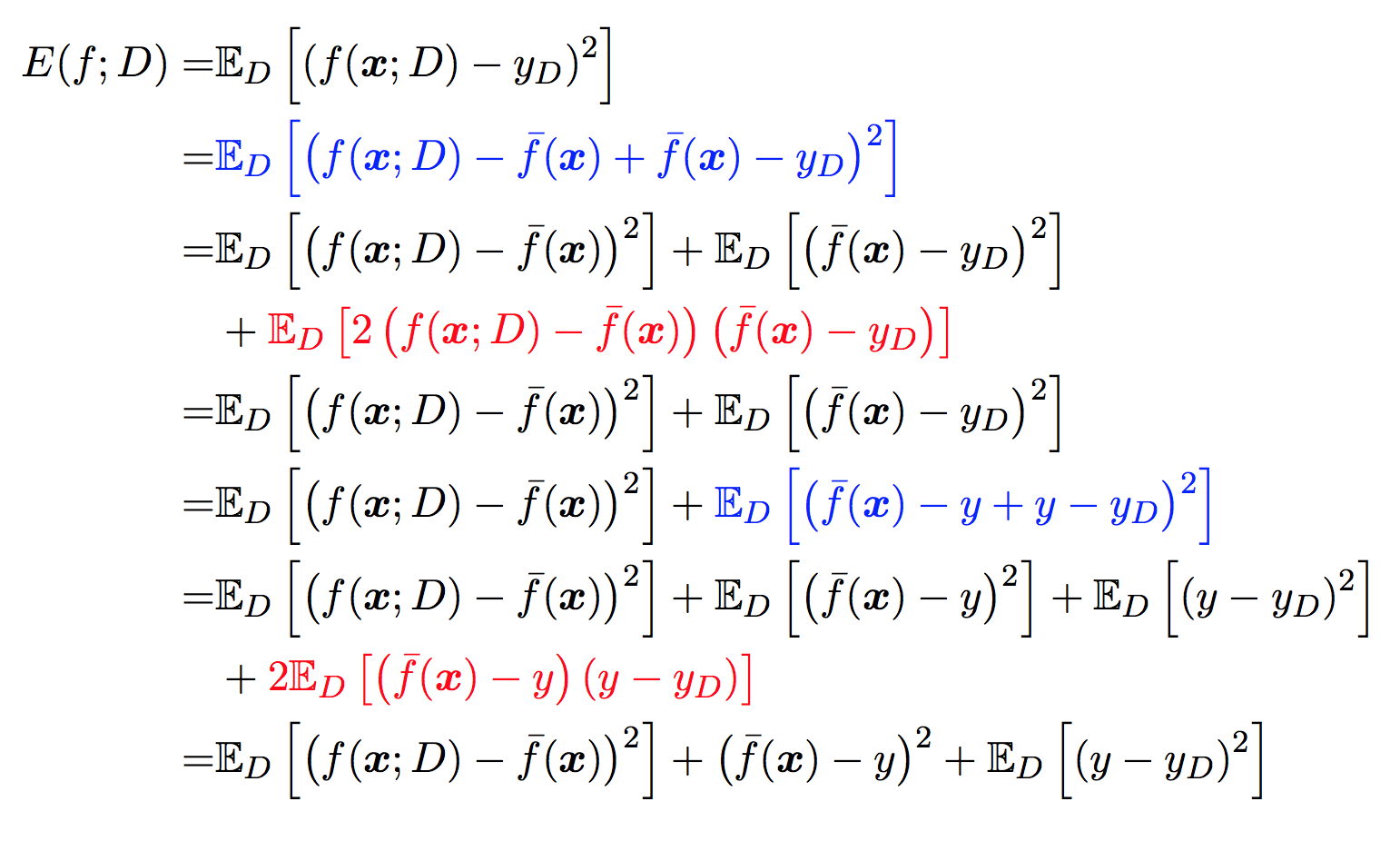
\[=Var(f(x;D))+bias^2(\bar{f}(\boldsymbol{x}))+\epsilon^2\]

其中应用到了$E_{D}[y_D -y]=0$和$E[f(x;D)]=\bar{f}(x)$。

实际应用时直接计算均方误差
\[MSE_ {train}=\frac{1}{m} \sum^m_{i=1}||y'_i-y_i||^2\]

学习算法的平方预测误差期望为(记$y'=f(x;D)$)²：
\[\begin{aligned}
Err(x)&=E[(y−f(x;D))^2]=E[(y−y')^2] \\
&=E[y'^2]-2E[yy']+E[y^2] \\
&=E[y'^2]-E(y')^2+E(y')^2-2yE[y']+y^2 \\
&=E[(y'-E(y'))^2]+[E(y')-y]^2 \\
&=Var(y')+bias(y')^2
\end{aligned} \tag{1}
\]

两者的差别在于：式$(1)$ 没有考虑$y_D$ 与 $y$ 之间的误差，这就是噪声。

源自《机器学习》周志华，第45页。个人更喜欢这个解释。↩
源自《深度学习》伊恩·古德费洛，第81页。↩