Unity3D 正六边形，环状扩散，紧密分布，的程序

最近在做一个正六边形的游戏，被一开始的布局难倒了。

需求：中心有个正六边形，输入围绕中心扩散的环数，自动创建和摆放。

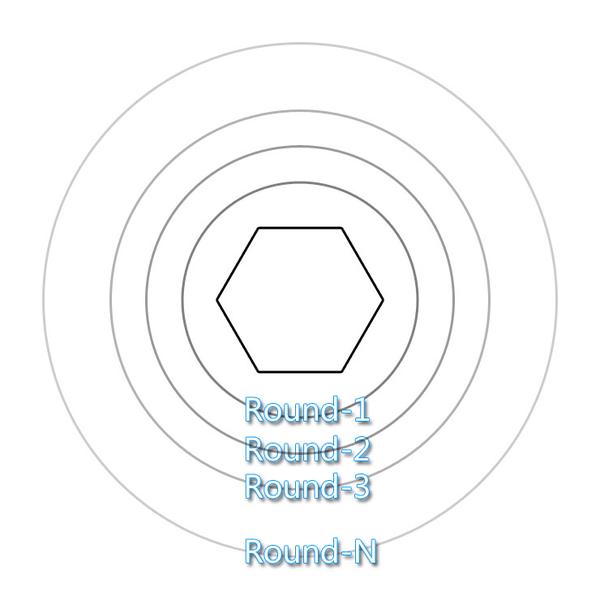
大概就是这样的吧，我觉得这个非常轻松的就可以搞定了。啊~~~~~啊~~~ 五环~~，你比四环多一环，啊~~~~啊~~~五环~~，你比六环少一环~~~

可是，到底每环要放多少个六边形？经过我缜密的观察发现一个规律。

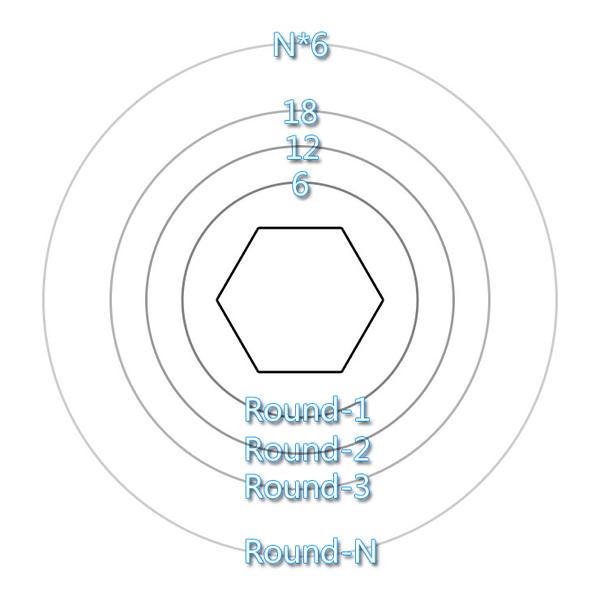
如果假设第一个环编号为1，那么每个换六边形的数量就是环数*6。啊~~~~~啊~~~ 五环~~，一环就是紫~禁~城~~~~。

可是摆放的具体位置是哪里？既然是圆形，那就需要知道角度和半径就可以依据圆形坐标公式算出来了。

二维圆上的点坐标公式:

X = Mathf.Sin(角度*Mathf.PI/180) * 半径

Y = Mathf.Cos(角度*Mathf.PI/180) * 半径

有人可能问，上面写的公式原理是啥？哈~哈~哈~~~~

啊~~~~~啊~~~ 五环~~，你比四环多一环，啊~~~~啊~~~五环~~~~~~

参见：已知圆心，半径，角度，求圆上的点坐标 - - 博客频道 - CSDN.NET

-----半径是啥？

紧密摆放的话，半径就是六边形的宽度。而每一环的半径就是环数*第一个半径。

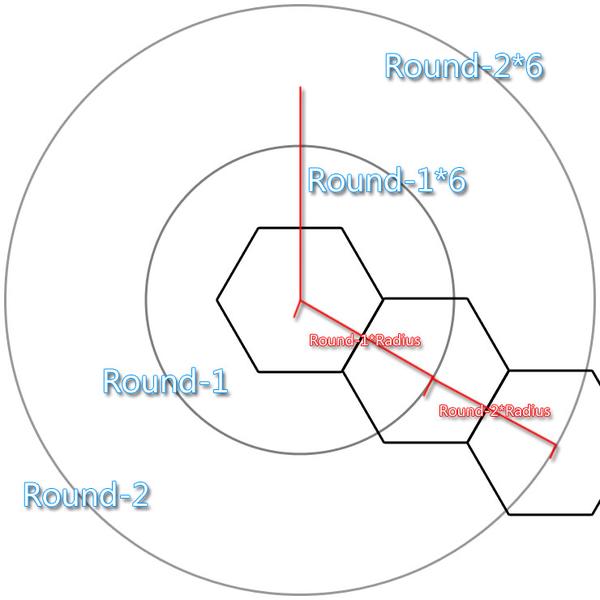
好了这个可以大概构建一个循环体了。

=========下面搭建循环体============

 Int RoundMax = ;//最大环数变量

 float Radius = 1f;//六边形最短宽度

 for（int round = ;round<=RoundMax;round++）//每一层环的循环体

 {

 for（环上每个六边形循环体）

 Vector2 = new Vector2(Mathf.Sin(角度*Mathf.PI/) * Radius * round, Mathf.Cos(角度*Mathf.PI/) * Radius * round);

 }

 }

===============

那么角度又是多少？

360 ÷ 每一环的总数 = 间隔的角度

间隔的角度 × 当前序号 = 当前角度

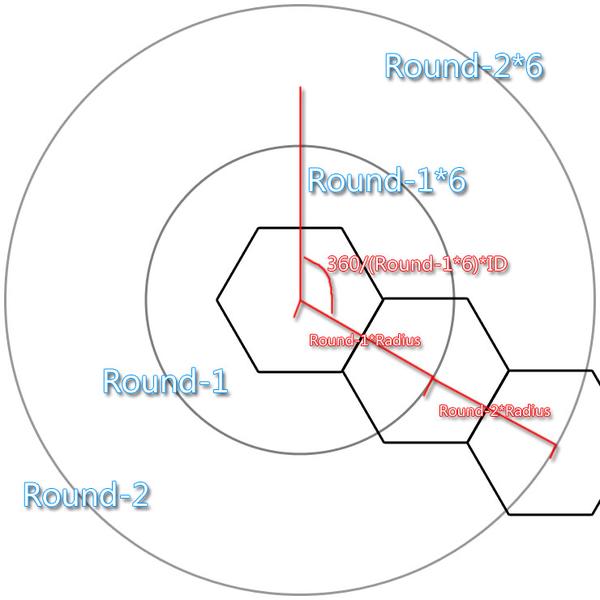
=========下面添加每一环的计算程序============

 Int RoundMax = ;//最大环数变量

 float Radius = 1f;//六边形最短宽度

 for（int round = ;round<=RoundMax;round++）//每一层环的循环体

 {

 for（int id = ; id<=round*; id++）//当前环的总个数 = round*6

 {

 Vector2 Pos= new Vector2(

 Mathf.Sin(/(round*)*id*Mathf.PI/) * Radius * round,

 Mathf.Cos(/(round*)*id*Mathf.PI/) * Radius * round

 );

 }

 }

=======下面转为三维向量========

 Int RoundMax = ;//最大环数变量

 float Radius = 1f;//六边形最短宽度

 for（int round = ;round<=RoundMax;round++）//每一层环的循环体

 {

 for（int id = ; id<=round*; id++）//当前环的总个数 = round*6

 {

 Vector3 Pos= new Vector3(

 Mathf.Sin(/(round*)*id*Mathf.PI/) * Radius * round,

 ，

 Mathf.Cos(/(round*)*id*Mathf.PI/) * Radius * round

 );

 }

 }

=====距离胜利还有一步下面引入模型和创建========

 GameObject Zero_OBJ;//六边形物体

 Int RoundMax = ;//最大环数变量

 float Radius = 1f;//六边形最短宽度

 for（int round = ;round<=RoundMax;round++）//每一层环的循环体

 {

 for（int id = ; id<=round*; id++）//当前环的总个数 = round*6

 {

 Vector3 Pos= new Vector3(

 Mathf.Sin(/(round*)*id*Mathf.PI/) * Radius * round + ,

 ，

 Mathf.Cos(/(round*)*id*Mathf.PI/) * Radius * round

 );

 Instantiate(Zero_OBJ,

 Zero_OBJ.transform.position.+ Pos ,//依据物体坐标偏移

 Quaternion.identity);

 }

 }

=======哈哈哈我是在佩服我的智慧========

天空飘来五个字那都不是事

运行结果

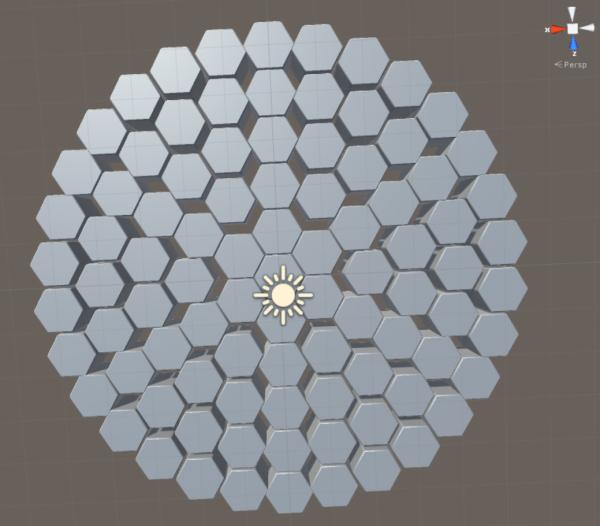
我去~~~真圆~~~~~

接下的十几分钟...

=================然后开始奋发图强的思考=============

其实还是有几个摆放正确的六边形

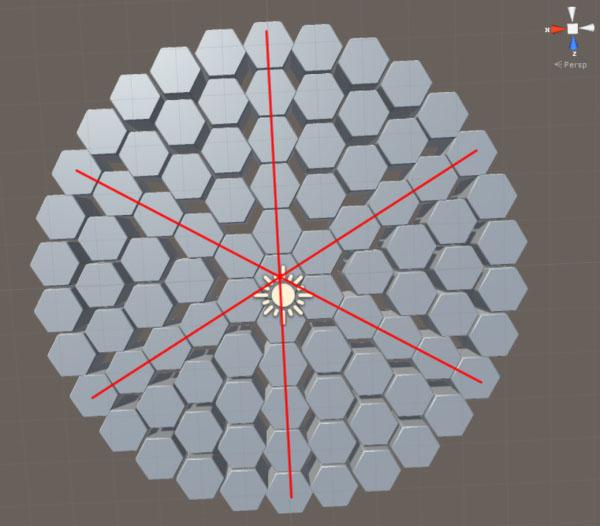
也就是说除了这0 , 60，120 , 180 , 240 , 300 角度的六边形，其余六边形其实不是正圆分布，而是直线分布。

如果是直线分布，就需要依据两点的坐标计算出排列的矢量方向，然后依据半径摆放就可以了。

=====接下吧正确位置写入 Pos_6[]========

 GameObject Zero_OBJ;//六边形物体

 Int RoundMax = ;//最大环数变量

 float Radius = 1f;//六边形最短宽度

 for（int round = ;round<=RoundMax;round++）//每一层环的循环体

 {

 int [] Pos_6 = new int[]；//记录正确6个位置的数组

 for（int id = ; id<= ; id++）//当前环的总个数 = round*6

 {

 Vector3 Pos_6[i]= new Vector3(

 Mathf.Sin(/(round*)*id*Mathf.PI/) * Radius * round + ,

 ，

 Mathf.Cos(/(round*)*id*Mathf.PI/) * Radius * round

 );

 Instantiate(Zero_OBJ,

 Zero_OBJ.transform.position.+ Pos_6[i] ,//依据物体坐标偏移

 Quaternion.identity);

 }

 }

中间的六边形个数规律是：

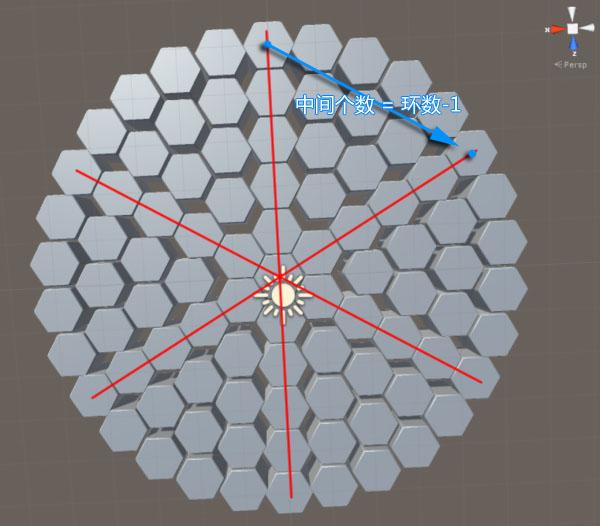
每个六边形偏移距离是：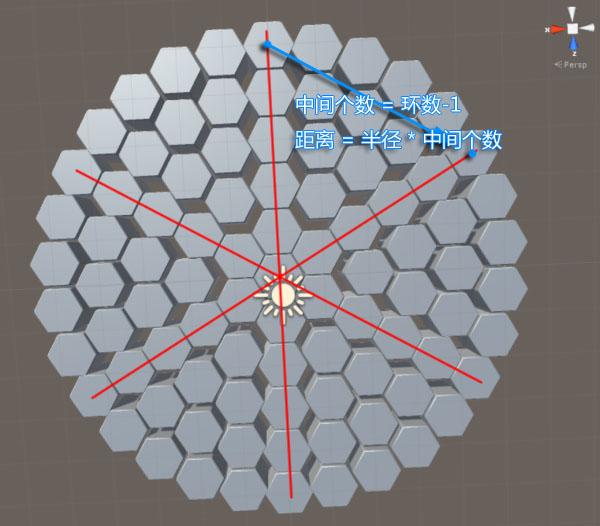

=======接下来插入之间的六边形========

 GameObject Zero_OBJ;//六边形物体

 Int RoundMax = ;//最大环数变量

 float Radius = 1f;//六边形最短宽度

 for（int round = ;round<=RoundMax;round++）//每一层环的循环体

 {

 int [] Pos_6 = new int[]；//记录正确6个位置的数组

 for（int id = ; id<= ; id++）

 {

 Vector3 Pos_6[i]= new Vector3(

 Mathf.Sin(/(round*)*id*Mathf.PI/) * Radius * round + ,

 ，

 Mathf.Cos(/(round*)*id*Mathf.PI/) * Radius * round

 );

 Instantiate(Zero_OBJ,

 Zero_OBJ.transform.position+ Pos_6[i] ,//依据物体坐标偏移

 Quaternion.identity);

 }

 if(round >)//第2圈开始执行插入

 {

 for（int id = ; id<= ; id++）//逐个区间插入

 {

 int NextID =( id+)%；//获取下一个位置ID，在0~5中循环取值

 Vector3 Orientation = Vector3.Normalize(Pos_6[id],Pos_6[NextID])//单位朝向（当前点，上一个点）

 for(int add = ;add<round-;add++)//循环插入

 {

 //----------插入点 = 单位方向*当前偏移距离+起点偏移

 Vector3 Now_Pos =

 Orientation

 *（Radius * add）

 +（ Pos_6[id] + Zero_OBJ.transform.position）；

 //-------------------------------------------------------------

 Instantiate(Zero_OBJ,Now_Pos,Quaternion.identity);

 }

 }

 }

 }

========运行结果===========

作者：CRomputer-罗军
链接：https://zhuanlan.zhihu.com/p/25243438
来源：知乎