MarkDown+LaTex 数学内容编辑样例收集

$\color{green}{MarkDown+LaTex 数学内容编辑样例收集}$

---

1、大小标题的居中，大小，颜色

【例1】

$\color{Blue}{一元二次方程根的分布}$

$\color{Red}{题型一：求数列{a_n}的通项公式} $

• $\color{red}{函数定义域}$

2、常见的数学符号

【例2】

大于等于 \(\ge\)；小于等于 \(\leq\)；不等于\(\neq\)；\(\Delta ABC\sim\Delta XYZ\)；\(\triangle ABC\)；角\(\angle A\)；\(\alpha \beta \gamma\)；

\(\sin\!\cfrac{\pi}{3}\) = \(\sin60^\circ\)=\(\cfrac{\sqrt{3}}{2}\)；正负\(\pm \mp\)； 间距4cm \(\angle A\) \(\hspace{4cm}\) \(\angle A\)

3、集合的相关符号

【例3】

\(m\)的取值范围为\(m\in \left\{ m\Big|\cfrac{1}{2}<m<\cfrac{2}{3} \right\}\) ；

任意 \(\forall\)；存在\(\exists\)； 空集\(\varnothing\)；属于\(\in \ni\)； 不属于\(\not\in\) \(\notin\) 真子集\(\subset\)

交集\(\cap\bigcap\)；并集\(\cup\bigcup\) 无穷大\(\infty\)

【例3’】

极限符号 \(\lim\limits_{x\to 1^+} f(x)=\lim\limits_{x\to 1^+}\cfrac{x}{x^2+3x+1}\) \(\hspace{2cm}\) 定积分符号 \(\int_{-1}^{2} e^x\, dx=e^2-e^{-1}\)

4、不等式组，方程组，线性约束条件组

【例4】不等式组\(\begin{cases} &-2 < m-1 < 2 \\\ &-2 <2m-1 <2 \\\ &m-1<1-2m\end{cases}\)

多个式子推出：\(\begin{gather*} f(x+4) &=-f(x) \\\ f(-x) &=-f(x)\end{gather*}\) \(\Bigg\}\Longrightarrow f(x+4)=f(-x)\Longrightarrow\)对称轴是\(x=2\)

\(\begin{align*} f(x+4) &=-f(x) \\\ f(-x) &=-f(x)\end{align*}\) \(\Bigg\}\Longrightarrow f(x+4)=f(-x)\Longrightarrow\)对称轴是\(x=2\)

5、分段函数
【例5】已知分段函数为：\(f(x) = \begin{cases}x^2 &x\leq 0 \\\ 3x+1 &x>0 \end{cases}\)

6、图像位置设置

【例6】(文字在左，图片在右的样例 )

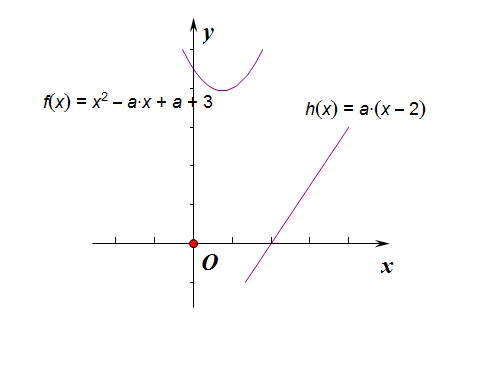
\(2^。\) 当\(a>0\)时，\(x_0<2\)时，\(g(x_0)<0\)，故只须\(x_0<2\)时，\(f(x_0)>2\)恒成立。

只需要\(\begin{cases} &a>0 \\\ &\Delta<0\end{cases}\) \(\hspace{4cm}\) 解得\(0<a<6\)

或者\(\begin{cases} &a>0 \\\ &\Delta\ge 0 \\\ &\cfrac{a}{2}>2 \\\ &f(2)=7-a\ge 0\end{cases}\) \(\hspace{2cm}\) 解得\(6\leq a\leq7\)。
故\(0<a\leq7\)

---

7、常用软件下载链接

OFFICE2007 3IN1 绿色版 http://oibd340aa.bkt.clouddn.com/Office2007.rar

MathsType http://oibd340aa.bkt.clouddn.com/MathType.rar

8、链接的使用

【数学交互素材】

9、答案的隐藏和显示

【示例题目】如已知\(2m+3n=2，m>0，n>0\)，求\(\cfrac{4}{m}+\cfrac{1}{n}\)的最小值。
分析如下：\(\cfrac{4}{m}+\cfrac{1}{n}=\cfrac{1}{2}\cdot (2m+3n）(\cfrac{4}{m}+\cfrac{1}{n})=\cfrac{1}{2}\cdot (8+3+\cfrac{2m}{n}+\cfrac{12n}{m})=\cdots\)

---