[Fundamental of Power Electronics]-PART II-8. 变换器传递函数-8.4 变换器传递函数的图形化构建

8.4 变换器传递函数的图形化构建

第7章推导出的buck变换器小信号等效电路模型在图8.55中再次给出。让我们用上一节的图解方法来构造该变换器的传递函数和端阻抗。

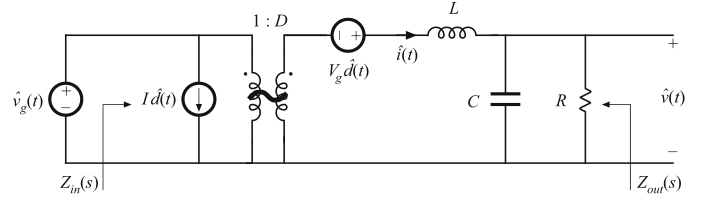
Fig. 8.55 Small-signal model of the buck converter, with input impedance Zin(s) and output impedance Zout(s) explicitly defined

输出阻抗\(Z_{out}(s)\)可以通过将\(\hat{d}(s)\)和\(\hat{v}_{g}(s)\)源设置为0而得到，如图8.56a。这个模型与8.3.3和8.3.4节中分析的并联\(R-L-C\)电路一致。如图8.56b所示，输出阻抗在低频由电感主导，高频由电容主导。谐振频率为：

\[f_{0}=\cfrac{1}{2\pi \sqrt{LC}} \tag{8.180}
\]

在频率\(f_{0}\)处，输出阻抗等于负载电阻\(R\)，电路的\(Q\)系数为：

\[Q=\cfrac{R}{R_{0}} \tag{8.181}
\]

其中：

\[R_{0}=\omega_{0} L=\cfrac{1}{\omega_{0}C}=\sqrt{\cfrac{L}{C}} \tag{8.182}
\]

因此，电路在R非常大的轻载下阻尼较小(高品质)。

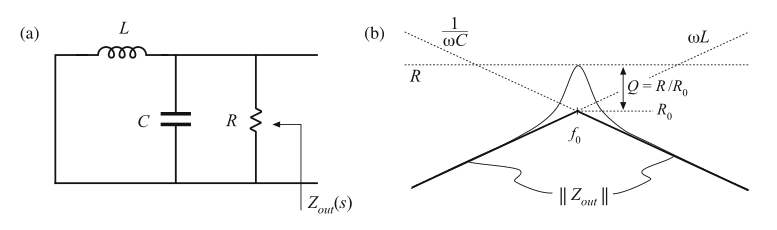
Fig. 8.56 Construction of buck converter output impedance Zout(s): (a) circuit model; (b) impedance

asymptotes

如图8.57a所示，变换器输入阻抗\(Z_{in}(s)\)也可以通过将\(\hat{d}(s)\)和\(\hat{v}_{g}(s)\)置零得到。输入阻抗指的是参考\(1:D\)变压器的初级侧，其等于：

\[Z_{in}(s)=\cfrac{1}{D^2}[Z_{1}(s)+Z_{2}(s)] \tag{8.183}
\]

其中：

\[Z_{1}(s)=sL \tag{8.184}
\]

并且：

\[Z_{2}(s)=R//\cfrac{1}{sC} \tag{8.185}
\]

如图：

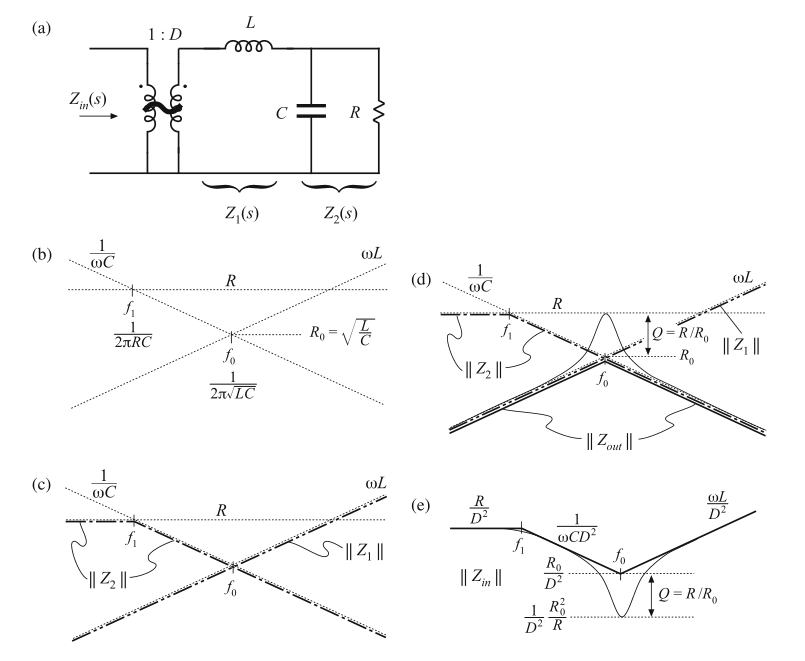
Fig. 8.57 Construction of the input impedance Zin(s) for the buck converter: (a) circuit model; (b) the individual resistor, inductor, and capacitor impedance magnitudes; (c) construction of the impedance magnitudes \(||Z_{1}||\) and \(||Z_{2}||\); (d) construction of \(||Z_{out}||\); (e) final result \(||Z_{in}||\)

我们可以开始利用图8.57b所示的单个电阻，电容和电感阻抗来构建对应式(8.183)到(8.185)的阻抗渐近线。图8.57中的阻抗是在\(R>R_{0}\)的情况下构建的。如图8.57c所示，\(||Z_{1}||\)与电感电抗\(\omega L\)一致。阻抗\(||Z_{2}||\)在低频趋近于电阻\(R\)，高频趋近于电容电抗\(1/\omega C\)。电阻和电容的阻抗渐近线交截于频率\(f_{1}\)，为：

\[f_{1}=\cfrac{1}{2\pi RC} \tag{8.186}
\]

根据式(8.183)，输入阻抗等于\(Z_{1}(s)\)和\(Z_{2}(s)\)的串联组合并除以匝比\(D\)的平方。串联组合\([Z_{1}(s)+Z_{2}(s)]\)的渐近线可以通过选择\(||Z_{1}||\)和\(||Z_{2}||\)中较大的那条渐近线来确定。\(||Z_{1}||\)和\(||Z_{2}||\)的渐近线在频率\(f_{0}\)处交截，这在式(8.180)。从图8.57c中可以看出，串联组合在\(f<f_{0}\)时由\(Z_{2}\)主导，而\(f>f_{0}\)处由\(Z_{1}\)主导。根据系数\(1/D^2\)对\([Z_{1}(s)+Z_{2}(s)]\)的渐近线进行缩放，获得了如图8.57e所示的输入阻抗渐近线。

\(Z_{in}(s)\)在频率\(f_{0}\)处的零点，与式(8.181)的\(Z_{out}(s)\)的极点具有相同的\(Q\)系数。证明这点的一个方法是将输出阻抗表示为：

\[Z_{out}(s)=\cfrac{Z_{1}(s)Z_{2}(s)}{Z_{1}(s)+Z_{2}(s)}=\cfrac{Z_{1}(s)Z_{2}(s)}{D^2 Z_{in}(s)} \tag{8.187}
\]

因此，\(Z_{in}(s)\)用来表示\(Z_{out}(s)\)为：

\[Z_{in}(s)=\cfrac{1}{D^2} \cfrac{Z_{1}(s)Z_{2}(s)}{Z_{out}(s)} \tag{8.188}
\]

\(||Z_{1}||\)，\(||Z_{2}||\)和\(||Z_{out}||\)的阻抗如图8.57d所示。在谐振频率\(f=f_{0}\)处，阻抗\(Z_{1}\)的幅值为\(R_{0}\)，阻抗\(Z_{2}\)的幅值近似为\(R_{0}\)。输出阻抗\(Z_{out}\)的幅值为\(R\)。根据式(8.188)，输入阻抗的幅值为：

\[||Z_{in}|| \approx \cfrac{1}{D^2} \cfrac{R_{0}R_{0}}{R}\ at\ f=f_{0} \tag{8.189}
\]

在\(f=f_{0}\)处，输入阻抗的渐近线幅值为\(R_{0}/D^2\)。如图8.57e所示，渐近线与实际值偏差为\(Q=R/R_{0}\)（译者：这里需要注意，这里的偏差并不是对数意义上的，是倍数关系)。

控制-输出传递函数\(G_{vd}(s)\)是通过将\(\hat{v}_{g}(s)\)源置零得到的，如图8.58a所示。这个电路与8.3.5节中的分压器电路是一致的，因此，\(G_{vd}(s)\)可以表示为：

\[G_{vd}(s)=V_{g} \cfrac{Z_{out}(s)}{Z_{1}(s)} \tag{8.190}
\]

图8.58b构建了\(||Z_{out}||\)和\(||Z_{1}||\)。根据式(8.190)，我们可以将\(||Z_{out}||\)和\(||Z_{1}||\)相除得到\(||G_{vd}(s)||\)，并将结果放大\(V_{g}\)倍。在\(f<f_{0}\)时，\(||Z_{out}||\)和\(||Z_{1}||\)都等于\(\omega L\)，因此\(||Z_{out}||/||Z_{1}||\)等于1。如图8.58c，\(||G_{vd}(s)||\)的低频渐近线的值为\(V_{g}\)。在\(f>f_{0}\)时，\(||Z_{out}||\)渐近线为\(1/\omega C\)，\(||Z_{1}||\)等于\(\omega L\)。因此\(||Z_{out}||/||Z_{1}||\)的渐近线为\(1/\omega^2 LC\)，并且\(||G_{vd}(s)||\)的高频渐近线等于\(V_{g}/\omega^2 LC\)。在\(f=f_{0}\)处的两极点的\(Q\)值仍然为\(R/R_{0}\)。

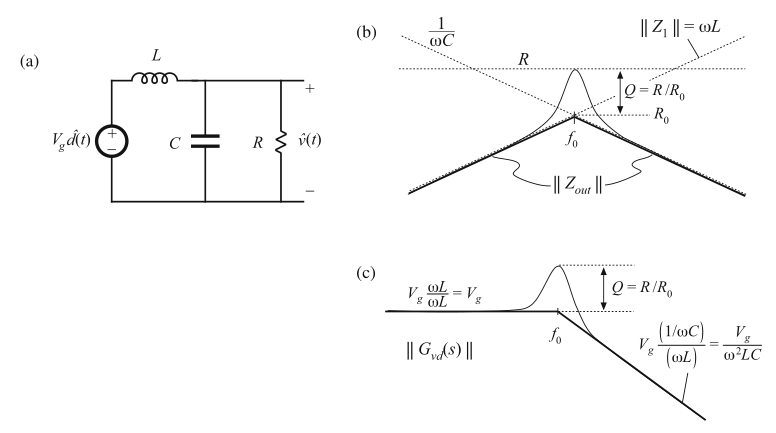
Fig. 8.58 Construction of the control-to-output transfer function \(G_{vd}(s)\) for the buck converter: (a) circuit model; (b) relevant impedance asymptotes; (c) transfer function \(||G_{vd}(s)||\)

如图8.59a，输入-输出传递函数\(G_{vg}(s)\)是将\(\hat{d}(s)\)源置零得到的。这个电路包含于图8.58中相同的分压器，同时还还有一个\(1:D\)的变压器。传递函数\(G_{vg}(s)\)可以表示为：

\[G_{vg}(s)=D \cfrac{Z_{out}(s)}{Z_{1}(s)} \tag{8.191}
\]

除了变比系数\(D\)，这个式子与(8.190)是类似的。因此，图8.59b的输入-输出传递函数具有与控制-输出传递函数\(G_{vd}(s)\)相同的形状

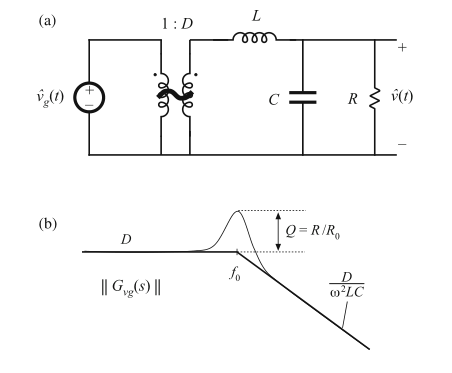
Fig. 8.59 The line-to-output transfer function \(G_{vg}(s)\) for the buck converter: (a) circuit model; (b) magnitude asymptotes