[Luogu P1268] 树的重量 (巧妙的构造题)

题面

传送门:https://www.luogu.org/problemnew/show/P1268

---

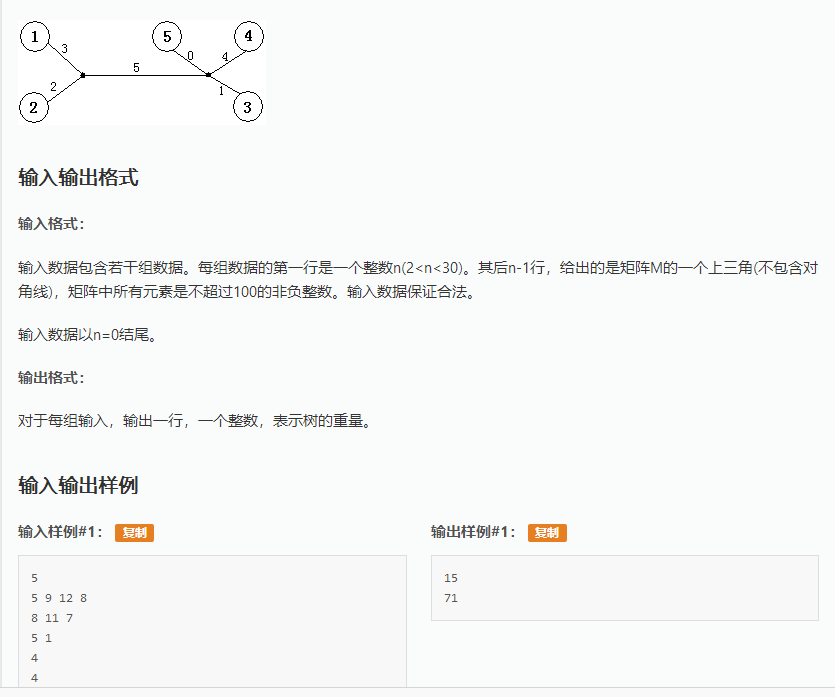
Solution

这是一道极其巧妙的构造题

先做一个约定[i,j]表示从i到j的距离

我们可以先从n=2,也就是最简单的情况来切入这道题

对于n=2,答案显然是[1,2]

接下来考虑n=3

如下图所示

这棵树一定是长成这样的

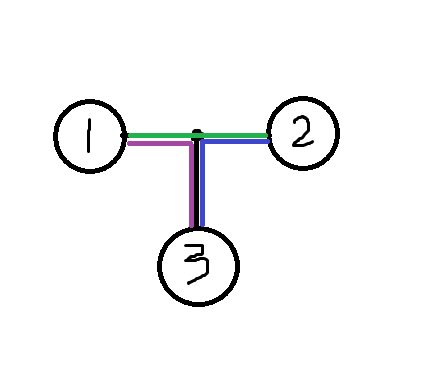
也就是说三这个节点一定是插在1与2两个节点之间的

我们可以发现,3节点的插入使得树的权值增加了([1,3]+[2,3]-[1,2])/2 (即紫线与蓝线的权值和减去绿线除以二)

我们可以把这个权值贡献的式子推广到一般情况

即x节点插入在[i,j]路径上

其对答案的贡献为([i,x]+[j,x]-[i,j])/2

接下来,我们继续把之前的结论推广到一般情况

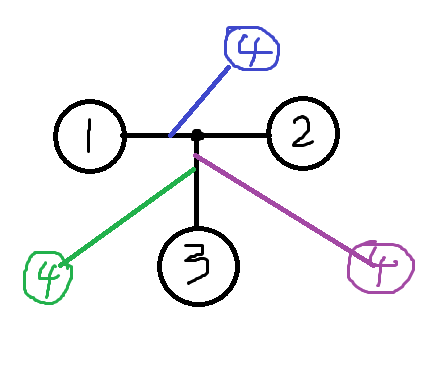
四号节点接下来是不是有可能加入在[1,2],[1,3],[2,3]这三条路径中

答案要求整棵树权值和尽可能小,我们只需要在三种情况中选最小值就好

我想你已经找到了一个O(n^3)的算法

就是枚举3~n的插入点,再用两层循环枚举所插入的边

复杂度O(n^3)

事实上,我们已经可以过这道题了.

但我们的复杂度还可以更优

重新再看一下这张图

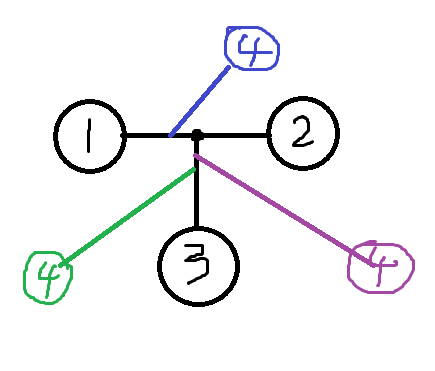
是不是可以发现我们紫色的那个其实是重复枚举

因为[1,4]+[3,4]-[1,3] 和[2,4]+[3,4]-[2,3] 其实都是一毛一样的!!!

这个结论也可以推广至一般状况中

所以说我们完全可以省去枚举中的一维

只枚举1~n就好

时间复杂度O(n^2)

---

Code

//Luogu P1268 树的重量
//May,30th,2018
//构造妙题
#include<iostream>
#include<cstdio>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const int N=30+5;
int n,a[N][N];
int main()
{
    while(1)
    {
        memset(a,0,sizeof a);
        int ans=0;
        n=read();
        if(n==0) break;
        for(int i=1;i<n;i++)
            for(int j=i+1;j<=n;j++)
                a[i][j]=a[j][i]=read();

        ans+=a[1][2];
        for(int i=3;i<=n;i++)
        {
            int t_ans=0x3f3f3f3f;
            for(int j=1;j<i;j++)
                for(int k=1;k<j;k++)
                    t_ans=min(t_ans,(a[j][i]+a[k][i]-a[j][k])/2);
            ans+=t_ans;
        }
        printf("%d\n",ans);
    }
    return 0;
}

正解(三方)(C++)

//Luogu P1268 树的重量
//May,30th,2018
//构造妙题
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const int N=30+5;
int n,a[N][N];
int main()
{
    while(1)
    {
        memset(a,0,sizeof a);
        int ans=0;
        n=read();
        if(n==0) break;
        for(int i=1;i<n;i++)
            for(int j=i+1;j<=n;j++)
                a[i][j]=a[j][i]=read();

        ans+=a[1][2];
        for(int i=3;i<=n;i++)
        {
            int t_ans=0x3f3f3f3f;
            for(int j=1;j<i;j++)
                t_ans=min(t_ans,(a[j][i]+a[1][i]-a[j][1])/2);
            ans+=t_ans;
        }
        printf("%d\n",ans);
    }
    return 0;
}

正解(平方)(C++)