hdu 6822 Paperfolding 规律+排列组合+逆元

题意：

给你一片纸，你可以对它进行四种操作，分别是向上、向下、向左、向右对折。把对折之后的纸片横向剪开，再纵向剪开（十字架剪开）

问你你能剪出来的纸片的期望个数

题解（参考：https://blog.csdn.net/fztsilly/article/details/107799718）：

很显然，向下和向上对折是一样的，向左和向右对折一样。那么也就变成了两种对折方式（这里为向下和向右）。选择其中某种方法可能性为1/2，同时对折的先后顺序不影响最后结果，即“右右下”和“下右右”对折后剪开的纸片数量一样

规律：往上下方向折k次，会有2^k条割线，那么横着切一刀展开后的纸片数有2^k+1张，这个+1就是最中间折痕左右两边纸片算一个，同理左右折。

假设折n次的情况下，设左右折次数为k，那么上下折次数为n−k。

那么总纸片数量为：(2^k+1)*(2^n-k+1)

因为折纸片的折叠操作顺序可以改变（“右右下”和“右下右”折出来的纸片数量都一样），所以这个结果应该乘于C^k_n ，又因为最后结果是期望，且一种操作执行概率为1/2，那么最后再乘于1/2ⁿ

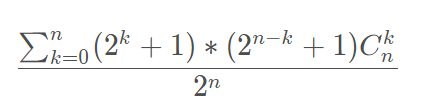
代码：

#include<stack>
#include<queue>
#include<map>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define fi first
#define se second
using namespace std;
typedef long long ll;
const int maxn=6e6+1;
const int mod=998244353;
const ll inv2 = 499122177;
ll quick_pow(ll a, ll b)
{
    ll ans = 1, base = a;
    while(b != 0)
    {
        if(b&1)
        {
            ans = ans * base;
            ans %= mod;
        }
        base = base * base % mod;
        b >>= 1;
    }
    return ans;
}
int main()
{
    ll t;
    cin >> t;
    while(t--)
    {
        ll n;
        cin >> n;
        if(n == 0)
        {
            cout << 4 << endl;
            continue;
        }
        ll k = (2 * quick_pow(3 * inv2 % mod, n) % mod + quick_pow(2, n) + 1) % mod;
        cout << k << endl;
    }
    return 0;
}