「IOI2017」接线 的另类做法

看到这题，我的第一反应是：这就是一个费用流模型？用模拟费用流的方法？

这应该是可以的，但是我忘记了怎么模拟费用流了IOI不可能考模拟费用流。于是我就想了另外一个方法。

首先我们考虑模拟费用流的模型如下图：

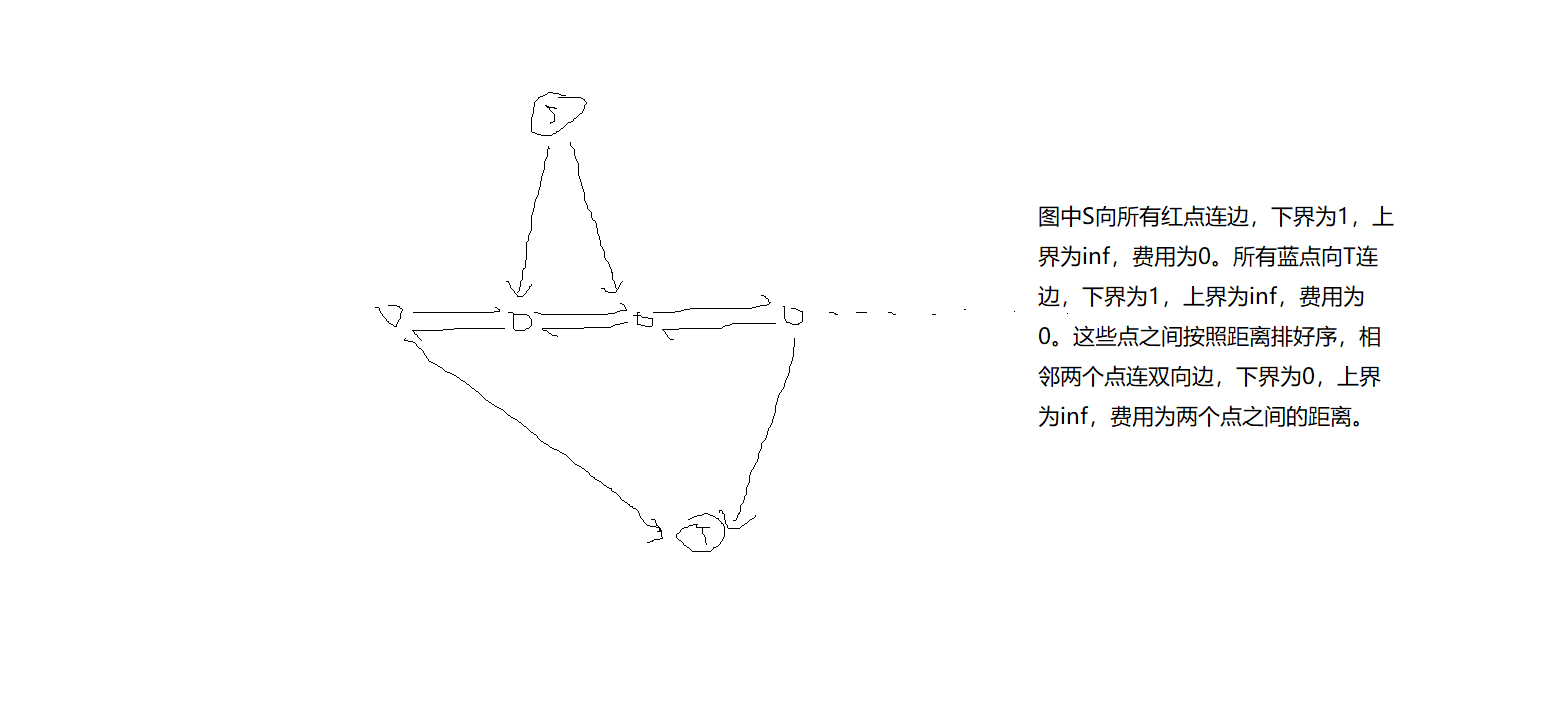
直接费用流复杂度比较大，我们把它换成一个dp。设\(f_{i, j}\)表示考虑了前\(i\)个点，且\(i\)个点后面一条在图中横着的边的流量为\(j\)的时候，最小费用是多少。注意这里从左到右的流量记为正，否则记为负。转移的时候如果第\(i\)个点是红点，就枚举\(S\)向这个点连的边的流量，否则枚举这个点向\(T\)连的边的流量。根据流量平衡方程我们算出前一条横着的边的流量。

用前缀/后缀min将这个算法优化至\(O((r + b)^2)\)，可以获得\(7\)分的成绩。

代码如下：

#include "wiring.h"
#include <bits/stdc++.h>
using namespace std;
const int N = 205, M = 205;
const long long inf = 1000000000000000ll;
int n, m;
long long f[N + M][N + M << 2], g[N + M][N + M << 2];
pair<long long, int> vec[N + M];
long long min_total_length(std::vector<int> r, std::vector<int> b) {
	n = r.size(), m = b.size();
	for (int i = 1; i <= n; i++) vec[i] = make_pair(r[i - 1], 0);
	for (int i = 1; i <= m; i++) vec[i + n] = make_pair(b[i - 1], 1);
	sort(vec + 1, vec + n + m + 1);
	for (int i = 0; i <= (n + m << 2); i++) f[0][i] = inf;
	f[0][n + m << 1] = 0ll;
	for (int i = 1; i <= n + m; i++) {
		for (int j = 0; j <= (n + m << 2); j++) {
			f[i][j] = f[i - 1][j];
			if (i) {
				int tim = j - (n + m << 1);
				if (tim < 0) tim = -tim;
				f[i][j] += 1ll * (vec[i].first - vec[i - 1].first) * tim;
			}
		}
		if (vec[i].second) {
			g[i][0] = f[i][0];
			for (int j = 1; j <= (n + m << 2); j++) g[i][j] = min(f[i][j], g[i][j - 1]);
			for (int j = 0; j <= (n + m << 2); j++) {
				if (!j) f[i][j] = inf;
				else f[i][j] = g[i][j - 1];
			}
		}
		else {
			g[i][n + m << 2] = f[i][n + m << 2];
			for (int j = (n + m << 2) - 1; j >= 0; j--) g[i][j] = min(f[i][j], g[i][j + 1]);
			for (int j = 0; j <= (n + m << 2); j++) {
				if (j == (n + m << 2)) f[i][j] = inf;
				else f[i][j] = g[i][j + 1];
			}
		}
	}
	return f[n + m][n + m << 1];
}

注意这里实现的时候用了平移的技巧处理第二维为负数的情况。

接下来我们考虑优化这个dp的方法。

把这个dp状态的第二维看成一个函数，那么我们会发现，需要进行的操作有：函数向左或向右平移一个单位，给它取前缀\(\min\)，给它取后缀\(\min\)，以及给它加上\(k \lvert x \rvert\)。

容易发现这些操作都不会改变函数下凸的性质。因此我们可以用APIO2016T2，我自己出的名为“穿越”的联测题等题目的方法。用一个set/multiset维护这个函数的每个拐点的位置以及斜率的变化值，再用\(O(1)\)的变量维护最左边/右边的那一段的斜率和截距，再维护偏移量（为了进行平移操作），就可以实现平移操作和加\(k \lvert x \rvert\)操作。而取前缀\(\min\)操作相当于是把一个函数图像的右边递增的一段变为常值函数，如下图所示：

因此我们可以在set/multiset上不断删除右边的拐点，直到右边那一段斜率刚好\(\ge 0\)（也就是再删去一个就\(<0\)了）为止。然后在改变恰好一个拐点的斜率变化量就可以实现前缀\(\min\)操作。同理我们可以实现后缀\(\min\)操作。

注意到这里的复杂度可以被拐点个数的减少量bound住，所以总复杂度仍然为\(O(n \log n)\)。

满分代码如下：

#include "wiring.h"
#include <bits/stdc++.h>
using namespace std;
const int N = 100005, M = 100005;
const long long inf = 1000000000ll;
int n, m;
pair<long long, int> vec[N + M];
multiset<pair<int, long long> > que;
long long min_total_length(std::vector<int> r, std::vector<int> b) {
	n = r.size(), m = b.size();
	for (int i = 1; i <= n; i++) vec[i] = make_pair(r[i - 1], 0);
	for (int i = 1; i <= m; i++) vec[i + n] = make_pair(b[i - 1], 1);
	sort(vec + 1, vec + n + m + 1);
	int val = 0;
	long long k_l = -inf, k_r = inf, val_l = inf * (n + m);
	que.insert(make_pair(0, inf << 1));
	for (int i = 1; i <= n + m; i++) {
		if (i > 1) {
			que.insert(make_pair(val, (vec[i].first - vec[i - 1].first) << 1));
			k_l -= vec[i].first - vec[i - 1].first, k_r += vec[i].first - vec[i - 1].first;
			val_l += (vec[i].first - vec[i - 1].first) * (n + m + val);
		}
		if (vec[i].second) {
			val++;
			while (k_l < 0ll) {
				pair<int, long long> pi = *que.begin();
				if (k_l + pi.second < 0ll) {
					val_l -= pi.second * (pi.first + n + m);
					k_l += pi.second;
				}
				else {
					val_l += k_l * (pi.first + n + m);
					que.insert(make_pair(pi.first, k_l + pi.second));
					k_l = 0ll;
				}
				que.erase(que.find(pi));
			}
		}
		else {
			val--;
			while (k_r > 0ll) {
				pair<int, long long> pi = *que.rbegin();
				if (k_r - pi.second > 0ll) k_r -= pi.second;
				else {
					que.insert(make_pair(pi.first, pi.second - k_r));
					k_r = 0ll;
				}
				que.erase(que.find(pi));
			}
		}
	}
	int lst = -n - m;
	long long ans = val_l;
	for (multiset<pair<int, long long> > :: iterator it = que.begin(); it != que.end(); it++) {
		pair<int, long long> pi = *it;
		if (pi.first < val) {
			ans += k_l * (pi.first - lst);
			k_l += pi.second, lst = pi.first;
		}
		else {
			ans += k_l * (val - lst);
			lst = val;
			break;
		}
	}
	if (lst < val) ans += k_l * (val - lst);
	return ans;
}