向量空间对加法封闭 对数乘封闭

直和：表示的唯一性

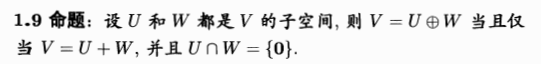
ALGEBRA-1 向量空间的更多相关文章

  1. 读Linear Algebra -- Gilbert Strang

    转眼间我的学士学位修读生涯已经快要到期了,重读线性代数,一是为了重新理解Algebra的的重要概念以祭奠大一刷过的计算题,二是为了将来的学术工作先打下一点点(薄弱的)基础.数学毫无疑问是指导着的科研方 ...

  2. 【线性代数】3-1:向量空间(Space of Vectors)

    title: [线性代数]3-1:向量空间(Space of Vectors) categories: Mathematic Linear Algebra keywords: Vectors Spac ...

  3. 【线性代数】Linear Algebra Big Picture

    Abstract: 通过学习MIT 18.06课程,总结出的线性代数的知识点相互依赖关系,后续博客将会按照相应的依赖关系进行介绍.(2017-08-18 16:28:36) Keywords: Lin ...

  4. Linear Algebra From Data

    Linear Algebra Learning From Data 1.1 Multiplication Ax Using Columns of A 有关于矩阵乘法的理解深入 矩阵乘法理解为左侧有是一 ...

  5. Linear Algebra lecture6 note

    Vector spaces and subspaces Column space of A solving Ax=b Null space of A   Vector space requiremen ...

  6. Linear Algebra Lecture5 note

    Section 2.7     PA=LU and Section 3.1   Vector Spaces and Subspaces   Transpose(转置) example: 特殊情况,对称 ...

  7. Linear Algebra lecture1 note

    Professor: Gilbert Strang Text: Introduction to Linear Algebra http://web.mit.edu/18.06   Lecture 1 ...

  8. 算法库：基础线性代数子程序库（Basic Linear Algebra Subprograms，BLAS）介绍

    调试DeepFlow光流算法,由于作者给出的算法是基于Linux系统的,所以要在Windows上运行,不得不做大量的修改工作.移植到Windows平台,除了一些头文件找不到外,还有一些函数也找不到.这 ...

  9. 《Linear Algebra and Its Applications》-chaper4-向量空间-子空间、零空间、列空间

    在线性代数中一个非常重要的概念就是向量空间R^n,这一章节将主要讨论向量空间的一系列性质. 一个向量空间是一些向量元素构成的非空集合V,需要满足如下公理: 向量空间V的子空间H需要满足如下三个条件: ...

  10. 《Linear Algebra and Its Applications》-chaper6-正交性和最小二乘法-基本概念与定理

    这一章节我们主要讨论定义在R^n空间上的向量之间的关系,而这个关系概括来讲其实就是正交,然后引入正交投影.最佳逼近定理等,这些概念将为我们在求无解的线性方程组Ax=b的最优近似解打下基石. 正交性: ...

随机推荐

  1. mysql间隙锁

    什么是间隙锁(gap lock)? 间隙锁是一个在索引记录之间的间隙上的锁. 间隙锁的作用? 保证某个间隙内的数据在锁定情况下不会发生任何变化.比如我mysql默认隔离级别下的可重复读(RR). 当使 ...

  2. nginx: command not found

    nginx 正常启动,可以访问服务器地址:welcome to nginx 使用nginx -t 等命令时 报错:nginx: command not found 这是环境变量未配置 配置环境变量 v ...

  3. 区间dp复习 之 乘积最大

    题目描述 今年是国际数学联盟确定的"2000--世界数学年",又恰逢我国著名数学家华罗庚先生诞辰90周年.在华罗庚先生的家乡江苏金坛,组织了一场别开生面的数学智力竞赛的活动,你的一 ...

  4. 题解 洛谷 P5324 【[BJOI2019]删数】

    先考虑对于一个序列,能使其可以删空的的修改次数. 首先可以发现,序列的排列顺序是没有影响的,所以可以将所有数放到桶里来处理. 尝试对一个没有经过修改的可以删空的序列来进行删数,一开始删去所有的\(n\ ...

  5. 前端学习（十六）：JavaScript运算

    进击のpython ***** 前端学习--JavaScript运算 在这一节之前,应该做到的是对上一节的数据类型的相关方法都敲一遍,加深印象 这部分的知识的特点就是碎而且杂,所以一定要多练~练习起来 ...

  6. Btree索引和Hash索引

    B-Tree 索引 BTree索引是最常用的mysql数据库索引算法,因为它不仅可以被用在=,>,>=,<,<=和between这些比较操作符上,而且还可以用于like操作符, ...

  7. Bug--时区问题导致IDEA连接数据库失败

    打开cmd进入mysql,设置 set global time_zone='+8:00';

  8. 每日一道 LeetCode (1)：两数之和

    引言 前段时间看到一篇刷 LeetCode 的文章,感触很深,我本身自己上大学的时候,没怎么研究过算法这一方面,导致自己直到现在算法都不咋地. 一直有心想填补下自己的这个短板,实际上又一直给自己找理由 ...

  9. nonlocal 访问变量

    def counter(start = 0): def incr(): nonlocal start #分别保存每一个变量的临时值.类似yield start += 1 return start re ...

  10. PHP gettimeofday() 函数

    ------------恢复内容开始------------ 实例 返回当前时间: <?php// Print the array from gettimeofday()print_r(gett ...