LDA主题模型困惑度计算

对于LDA模型，最常用的两个评价方法困惑度（Perplexity）、相似度（Corre）。

其中困惑度可以理解为对于一篇文章d，所训练出来的模型对文档d属于哪个主题有多不确定，这个不确定成都就是困惑度。困惑度越低，说明聚类的效果越好。

计算公式 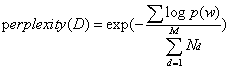    分母是测试集中所有单词之和，即测试集的总长度，不用排重。其中p(w)指的是测试集中每个单词出现的概率，计算公式如下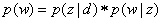。p(z|d)表示的是一个文档中每个主题出现的概率，就是程序中的.theta文件，p(w|z)表示的是词典中的每一个单词在某个主题下出现的概率，就是程序中的.phi文件。

 1 public void getRe(double[][] phi, double[][] theta){
 2         double count = 0;
 3         int i = 0;
 4         Iterator iterator = userWords.entrySet().iterator();
 5         while(iterator.hasNext()){
 6             Map.Entry entry = (Map.Entry) iterator.next();
 7             ArrayList<String> list = (ArrayList<String>) entry.getValue();
 8             double mul = 0;
 9             for(int j = 0; j < list.size(); j++){
10                 double sum = 0;
11                 String word = list.get(j);
12                 int index = wordMap.get(word);
13                 for (int k = 0; k < K; k++){
14                     sum = sum + phi[k][index] * theta[i][k];
15                 }
16                 mul = mul + Math.log(sum);
17             }
18             count = count + mul;
19             i++;
20         }
21         count = 0 - count;
22         P = Math.exp(count / N);
23         System.out.println("Perplexity:" + P);

对于不同Topic所训练出来的模型，计算它的困惑度。最小困惑度所对应的Topic就是最优的主题数。