force

题意

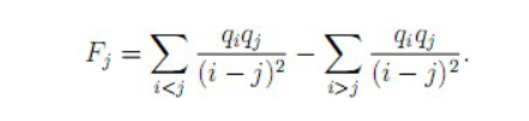
求解 Ei = Fi/qi

解法：

方法一：

考虑左侧的式子，直接多项式乘法。

对于右面的式子，我们记做$B_j$，这样有

$$B_j = \sum_{j<i}{ revq_{n-i} f(i-j) }$$

$$B_j = \sum_{0<k<n-j}{ revq_t f(n-j-t) }$$

$$B_j = (revq \otimes f)_{n-j}$$

五次DFT变形即可。

在卡精度的情况下可以用实时用三角函数算 $wt$ 代替用 $wn$ 连乘旋转得到 $wt$。

#include <bits/stdc++.h>

#define PI acos(-1)

const int N = ;

using namespace std;

struct EX
{
    double real,i;
    EX operator+(const EX tmp)const{return (EX){real+tmp.real, i+tmp.i};};
    EX operator-(const EX tmp)const{return (EX){real-tmp.real, i-tmp.i};};
    EX operator*(const EX tmp)const{return (EX){real*tmp.real - i*tmp.i, real*tmp.i + i*tmp.real};};
};

int R[N<<];

void DFT(EX a[],int n,int tp_k)
{
    for(int i=;i<n;i++) if(i<R[i]) swap(a[i],a[R[i]]);
    for(int d=;d<n;d<<=)
    {
        EX wn = (EX){cos(PI/d), sin(PI/d)*tp_k};
        for(int i=;i<n;i += (d<<))
        {
            EX wt = (EX){,};    //高速度用
            for(int k=;k<d;k++, wt = wt*wn)
            {
            //    EX wt = (EX){cos(PI*k / d) ,tp_k*sin(PI*k / d)}; //高精度用（到 10^14 的精度）
                EX A0 = a[i+k], A1 = wt * a[i+k+d];
                a[i+k] = A0+A1;
                a[i+k+d] = A0-A1;
            }
        }
    }
    if(tp_k==-)
        for(int i=;i<n;i++) a[i] = (EX){a[i].real/n, a[i].i/n};
}

int n,m;
EX A[N<<],B[N<<],C[N<<];
double q[N],ans[N];

int main()
{
    freopen("force.in", "r", stdin);
    freopen("force.out", "w", stdout);
    scanf("%d",&n);
    for(int i=;i<n;i++) scanf("%lf",&q[i]);
    int L = ,tot;
    while((<<L)<n+n-) L++;
    tot = (<<L);
    for(int i=;i<tot;i++) R[i]=(R[i>>]>>)|((i&)<<(L-));

    for(int i=;i<n;i++) A[i] = (EX){q[i], };
    for(int i=;i<n;i++) B[i] = (EX){/(double)i/(double)i, };
    DFT(A,tot,);
    DFT(B,tot,);
    for(int i=;i<tot;i++) C[i] = A[i]*B[i];
    DFT(C,tot,-);
    for(int i=;i<n;i++) ans[i] += C[i].real;

    memset(A,,sizeof(A));
    for(int i=;i<n;i++) A[i] = (EX){q[n-i], };
    DFT(A,tot,);
    for(int i=;i<tot;i++) C[i] = A[i]*B[i];
    DFT(C,tot,-);
    for(int i=;i<n;i++) ans[i] -= C[n-i].real;

    for(int i=;i<n;i++) printf("%.3lf\n",ans[i]);
    return ;
}

方法二：

考虑拓展

$$C_{j+n} = \sum_{0 \leq k \leq j+n} { q_k A_{j+n-k} }$$

其中

$A_i = \frac{1}{(i-n)^2} (n < i < 2n)$

$A_i = \frac{1}{(n-i)^2} (0 < i < n)$

从而有 $B_j = C_{j+n}$

其他全为0，这样一次FFT卷积得到答案

#include <bits/stdc++.h>

#define PI acos(-1)

const int N = ;

using namespace std;

struct EX
{
    double real,i;
    EX operator+(const EX tmp)const{return (EX){real+tmp.real, i+tmp.i};};
    EX operator-(const EX tmp)const{return (EX){real-tmp.real, i-tmp.i};};
    EX operator*(const EX tmp)const{return (EX){real*tmp.real - i*tmp.i, real*tmp.i + i*tmp.real};};
};

int R[N<<];

void DFT(EX a[],int n,int tp_k)
{
    for(int i=;i<n;i++) if(i<R[i]) swap(a[i],a[R[i]]);
    for(int d=;d<n;d<<=)
    {
        EX wn = (EX){cos(PI/d), sin(PI/d)*tp_k};
        for(int i=;i<n;i += (d<<))
        {
            EX wt = (EX){,};    //高速度用
            for(int k=;k<d;k++, wt = wt*wn)
            {
            //    EX wt = (EX){cos(PI*k / d) ,tp_k*sin(PI*k / d)}; //高精度用（到 10^14 的精度）
                EX A0 = a[i+k], A1 = wt * a[i+k+d];
                a[i+k] = A0+A1;
                a[i+k+d] = A0-A1;
            }
        }
    }
    if(tp_k==-)
        for(int i=;i<n;i++) a[i] = (EX){a[i].real/n, a[i].i/n};
}

int n,m;
EX A[N<<],B[N<<],C[N<<];
double q[N],ans[N];

int main()
{
    freopen("force.in", "r", stdin);
    freopen("force.out", "w", stdout);
    scanf("%d",&n);
    for(int i=;i<n;i++) scanf("%lf",&q[i]);
    int L = ,tot;
    while((<<L)<*n-) L++;
    tot = (<<L);
    for(int i=;i<tot;i++) R[i]=(R[i>>]>>)|((i&)<<(L-));

    for(int i=;i<n;i++) A[i] = (EX){q[i], };
    for(int i=;i<n;i++)
    {
        B[i] = (EX){-/(double)(n-i)/(double)(n-i), };
        B[i+n] = (EX){/(double)i/(double)i, };
    }
    DFT(A,tot,);
    DFT(B,tot,);
    for(int i=;i<tot;i++) C[i] = A[i]*B[i];
    DFT(C,tot,-);
    for(int i=;i<n;i++) ans[i] = C[i+n].real;
    for(int i=;i<n;i++) printf("%.3lf\n",ans[i]);
    return ;
}