Codeforces Round #323 (Div. 2) C 无敌gcd 数学/贪心

C. GCD Table

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The GCD table G of size n × n for an array of positive integers a of length n is defined by formula

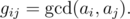
Let us remind you that the greatest common divisor (GCD) of two positive integers x and y is the greatest integer that is divisor of both x and y, it is denoted as 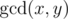. For example, for array a = {4, 3, 6, 2} of length 4 the GCD table will look as follows:

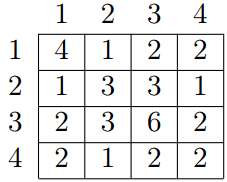
Given all the numbers of the GCD table G, restore array a.

Input

The first line contains number n (1 ≤ n ≤ 500) — the length of array a. The second line contains n² space-separated numbers — the elements of the GCD table of G for array a.

All the numbers in the table are positive integers, not exceeding 10⁹. Note that the elements are given in an arbitrary order. It is guaranteed that the set of the input data corresponds to some array a.

Output

In the single line print n positive integers — the elements of array a. If there are multiple possible solutions, you are allowed to print any of them.

Examples

Input

4
2 1 2 3 4 3 2 6 1 1 2 2 1 2 3 2

Output

4 3 6 2

Input

1
42

Output

42 

Input

2
1 1 1 1

Output

1 1 

题意： n个数 形成了n*n的 gcd表格

现在乱序给你这n*n的 gcd表格 要求你输出这n个数

题解：因为两个数字的最大公因数一定小于这两个数，所以n*n中最大的两个数字一定在主对角线上，然后排除掉他们的最大公因数后找剩余数字最大的数字，继续排除已知数字的最大公因数，直到找出n个数字为止。这种构造方法的有效性可以证明贪心策略的正确性，注意去掉已知的数字的最大公因数每次-2

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<queue>
 #include<stack>
 #include<vector>
 #include<map>
 #include<algorithm>
 #define ll __int64
 #define mod 1e9+7
 #define PI acos(-1.0)
 using namespace std;
 int n;
 int a[];
 map<int,int>mp;
 vector<int> ve;
 int gcd(int aa,int bb)
 {
     if(bb==)
         return aa;
     else
     return gcd(bb,aa%bb);
 }
 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n*n;i++)
     {
         scanf("%d",&a[i]);
         mp[a[i]]++;
     }
     sort(a+,a+n*n+);
     for(int i=n*n;i;i--)
     {
         if(!mp[a[i]])
             continue;
         mp[a[i]]--;
         for(int j=;j<ve.size();j++)
             mp[gcd(ve[j],a[i])]-=;
         ve.push_back(a[i]);
     }
     for(int i=;i<=n-;i++)
         cout<<ve[i]<<" ";
     cout<<endl;
 }