ACM-ICPC 2018 南京赛区网络预赛

轻轻松松也能拿到区域赛名额，CCPC真的好难

An Olympian Math Problem

只看题面

54.76%
1000ms
65536K

Alice, a student of grade 66, is thinking about an Olympian Math problem, but she feels so despair that she cries. And her classmate, Bob, has no idea about the problem. Thus he wants you to help him. The problem is:

We denote k!k!:

k! = 1 \times 2 \times \cdots \times (k - 1) \times kk!=1×2×⋯×(k−1)×k

We denote SS:

S = 1 \times 1! + 2 \times 2! + \cdots +S=1×1!+2×2!+⋯+
(n - 1) \times (n-1)!(n−1)×(n−1)!

Then SS module nn is ____________

You are given an integer nn.

You have to calculate SS modulo nn.

Input

The first line contains an integer T(T \le 1000)T(T≤1000), denoting the number of test cases.

For each test case, there is a line which has an integer nn.

It is guaranteed that 2 \le n\le 10^{18}2≤n≤1018.

Output

For each test case, print an integer SSmodulo nn.

Hint

The first test is: S = 1\times 1!= 1S=1×1!=1, and 11modulo 22 is 11.

The second test is: S = 1\times 1!+2 \times 2!= 5S=1×1!+2×2!=5 , and 55modulo 33 is 22.

样例输入复制

样例输出复制

1

2

题目来源

ACM-ICPC 2018 南京赛区网络预赛

A题在抢首A的道路上努力奔跑，然后CE

输出n-1，因为( p -1 )! ≡ -1 ( mod p )威尔逊定理

#include<stdio.h>

#include<bits/stdc++.h>

using namespace std;

#define lson l,(l+r)/2,rt<<1

#define rson (l+r)/2+1,r,rt<<1|1

#define dbg(x) cout<<#x<<" = "<< (x)<< endl

#define pb push_back

#define fi first

#define se second

#define ll long long

#define sz(x) (int)(x).size()

#define pll pair<long long,long long>

#define pii pair<int,int>

#define pq priority_queue

const int N=1e5+,MD=1e9+,INF=0x3f3f3f3f;

const ll LL_INF=0x3f3f3f3f3f3f3f3f;

const double eps=1e-,e=exp(),PI=acos(-.);

int main()

{

    ios::sync_with_stdio(false),cin.tie(),cout.tie();

    int T;

    cin>>T;

    while(T--)

    {

        ll n;

        cin>>n;

        cout<<n-<<"\n";

    }

    return ;

}

The writing on the wall

Feeling hungry, a cute hamster decides to order some take-away food (like fried chicken for only 3030 Yuan).

However, his owner CXY thinks that take-away food is unhealthy and expensive. So she demands her hamster to fulfill a mission before ordering the take-away food. Then she brings the hamster to a wall.

The wall is covered by square ceramic tiles, which can be regarded as a n * mn∗mgrid. CXY wants her hamster to calculate the number of rectangles composed of these tiles.

For example, the following 3 * 33∗3 wall contains 3636 rectangles:

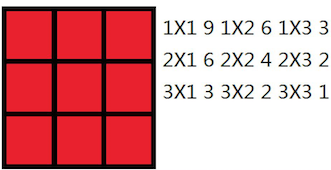
Such problem is quite easy for little hamster to solve, and he quickly manages to get the answer.

Seeing this, the evil girl CXY picks up a brush and paint some tiles into black, claiming that only those rectangles which don't contain any black tiles are valid and the poor hamster should only calculate the number of the valid rectangles. Now the hamster feels the problem is too difficult for him to solve, so he decides to turn to your help. Please help this little hamster solve the problem so that he can enjoy his favorite fried chicken.

Input

There are multiple test cases in the input data.

The first line contains a integer TT : number of test cases. T \le 5T≤5.

For each test case, the first line contains 33integers n , m , kn,m,k , denoting that the wall is a n \times mn×m grid, and the number of the black tiles is kk.

For the next kk lines, each line contains 22integers: x\ yx y ,denoting a black tile is on the xx-th row and yy-th column. It's guaranteed that all the positions of the black tiles are distinct.

For all the test cases,

1 \le n \le 10^5,1\le m \le 1001≤n≤105,1≤m≤100,

0 \le k \le 10^5 , 1 \le x \le n, 1 \le y \le m0≤k≤105,1≤x≤n,1≤y≤m.

It's guaranteed that at most 22 test cases satisfy that n \ge 20000n≥20000.

Output

For each test case, print "Case #xx: ansans" (without quotes) in a single line, where xxis the test case number and ansans is the answer for this test case.

Hint

The second test case looks as follows:

样例输入复制

样例输出复制

Case #1: 36

Case #2: 20

题目来源

ACM-ICPC 2018 南京赛区网络预赛

B是个51nod的原题，可以用单调栈维护，维护出这样一个玩意

然后就可以前缀和

#include<stdio.h>

#include<bits/stdc++.h>

using namespace std;

#define lson l,(l+r)/2,rt<<1

#define rson (l+r)/2+1,r,rt<<1|1

#define dbg(x) cout<<#x<<" = "<< (x)<< endl

#define pb push_back

#define fi first

#define se second

#define ll long long

#define sz(x) (int)(x).size()

#define pll pair<long long,long long>

#define pii pair<int,int>

#define pq priority_queue

const int N=1e5+,MD=1e9+,INF=0x3f3f3f3f;

const ll LL_INF=0x3f3f3f3f3f3f3f3f;

const double eps=1e-,e=exp(),PI=acos(-.);

using namespace std;

bool s[N][];

ll a[N][];

int b[N],sta[N],L[N],R[N],T[N];

int n, m;

int main()

{

    ios::sync_with_stdio(false),cin.tie(),cout.tie();

    int cc;

    cin>>cc;

    for(int ca=;ca<=cc;ca++)

    {

        int n,m,k;

        cin>>n>>m>>k;

        for(int i=; i<=n; i++)for(int j=; j<=m; j++)s[i][j]=;

        for(int i=,x,y; i<k; i++)cin>>x>>y,s[x][y]=;

        memset(a,,sizeof a),memset(b,,sizeof b);

        b[]=b[m+]=-;

        for(int i=,tot; i<=n; i++)

        {

            tot=-;

            sta[++tot]=;

            for(int j=; j<=m; j++)

            {

                if(s[i][j]==)++b[j];

                else b[j]=;

                while(b[sta[tot]]>b[j])--tot;

                T[j]=sta[tot];

                while(b[sta[tot]]>=b[j])--tot;

                L[j]=sta[tot],sta[++tot]=j;

            }

            tot=-;

            sta[++tot]=m+;

            for(int j=m; j>; j--)

            {

                while(b[sta[tot]]>=b[j])--tot;

                R[j]=sta[tot],sta[++tot]=j;

            }

            for(int j=,s,t; j<=m; j++)

            {

                if(b[j]&&b[T[j]]!=b[j])

                {

                    s=max(,max(b[L[j]],b[R[j]])+),t=R[j]-L[j]-;

                    if(s>b[j]) continue;

                    ++a[s][t],--a[b[j]+][t];

                }

            }

        }

        ll ans=,tt,t;

        for(int i=; i<=n; i++)for(int j=; j<=m; j++)a[i][j]+=a[i-][j];

        for(int i=; i<=n; i++)

        {

            tt=;

            for(int j=m; j>; j--)t=a[i][j],a[i][j]+=a[i][j+]+tt,tt+=t;

            for(int j=; j<=m; j++)ans+=a[i][j];

        }

        cout<<"Case #"<<ca<<": "<<ans<<"\n";

    }

    return ;

}

AC Challenge

Dlsj is competing in a contest with n (0 < n \le 20)n(0<n≤20) problems. And he knows the answer of all of these problems.

However, he can submit ii-th problem if and only if he has submitted (and passed, of course) s_isi problems, the p_{i, 1}pi,1-th, p_{i, 2}pi,2-th, ......, p_{i, s_i}pi,si-th problem before.(0 < p_{i, j} \le n,0 < j \le s_i,0 < i \le n)(0<pi,j≤n,0<j≤si,0<i≤n)After the submit of a problem, he has to wait for one minute, or cooling down time to submit another problem. As soon as the cooling down phase ended, he will submit his solution (and get "Accepted" of course) for the next problem he selected to solve or he will say that the contest is too easy and leave the arena.

"I wonder if I can leave the contest arena when the problems are too easy for me."
"No problem."
—— CCF NOI Problem set

If he submits and passes the ii-th problem on tt-th minute(or the tt-th problem he solve is problem ii), he can get t \times a_i + b_it×ai+bi points. (|a_i|, |b_i| \le 10^9)(∣ai∣,∣bi∣≤109).

Your task is to calculate the maximum number of points he can get in the contest.

Input

The first line of input contains an integer, nn, which is the number of problems.

Then follows nn lines, the ii-th line contains s_i + 3si+3 integers, a_i,b_i,s_i,p_1,p_2,...,p_{s_i}ai,bi,si,p1,p2,...,psias described in the description above.

Output

Output one line with one integer, the maximum number of points he can get in the contest.

Hint

In the first sample.

On the first minute, Dlsj submitted the first problem, and get 1 \times 5 + 6 = 111×5+6=11points.

On the second minute, Dlsj submitted the second problem, and get 2 \times 4 + 5 = 132×4+5=13 points.

On the third minute, Dlsj submitted the third problem, and get 3 \times 3 + 4 = 133×3+4=13points.

On the forth minute, Dlsj submitted the forth problem, and get 4 \times 2 + 3 = 114×2+3=11points.

On the fifth minute, Dlsj submitted the fifth problem, and get 5 \times 1 + 2 = 75×1+2=7points.

So he can get 11+13+13+11+7=5511+13+13+11+7=55 points in total.

In the second sample, you should note that he doesn't have to solve all the problems.

样例输入1复制

样例输出1复制

样例输入2复制

1

-100 0 0

样例输出2复制

题目来源

ACM-ICPC 2018 南京赛区网络预赛

有几个属性，但是你看了n给了20就要知道要状压dp，1<<20是1024*1024

#include <bits/stdc++.h>

using namespace std;

int dp[<<],a[],b[],S[];

int f(int x)

{

    int ans=;

    while(x)

    {

        x-=x&-x;

        ans++;

    }

    return ans;

}

int main()

{

    int n;

    scanf("%d",&n);

    for(int i=,m;i<n;i++)

    {

        scanf("%d%d%d",&a[i],&b[i],&m);

        for(int j=,x;j<m;j++)

            scanf("%d",&x),S[i]|=(<<(x-));

    }

    //for(int i=0;i<n;i++)

    //    printf("%d\n",S[i]);

    memset(dp,-,sizeof dp);

    dp[]=;

    for(int s=;s<<<n;s++)

    {

        if(dp[s]==-) continue;

        for(int i=;i<n;i++)

            if((s&S[i])==S[i]&&(s&(<<i))==)

                dp[s|(<<i)]=max(dp[s|(<<i)],dp[s]+a[i]*(f(s)+)+b[i]);

    }

    int ans=;

    for(int i=;i<<<n;i++)

        ans=max(ans,dp[i]);

    printf("%d\n",ans);

    return ;

}

Sum

问答

只看题面

26.14%
1000ms
512000K

A square-free integer is an integer which is indivisible by any square number except 11. For example, 6 = 2 \cdot 36=2⋅3 is square-free, but 12 = 2^2 \cdot 312=22⋅3 is not, because 2^222 is a square number. Some integers could be decomposed into product of two square-free integers, there may be more than one decomposition ways. For example, 6 = 1\cdot 6=6 \cdot 1=2\cdot 3=3\cdot 2, n=ab6=1⋅6=6⋅1=2⋅3=3⋅2,n=aband n=ban=ba are considered different if a \not = ba̸=b. f(n)f(n) is the number of decomposition ways that n=abn=ab such that aa and bb are square-free integers. The problem is calculating \sum_{i = 1}^nf(i)∑i=1nf(i).

Input

The first line contains an integer T(T\le 20)T(T≤20), denoting the number of test cases.

For each test case, there first line has a integer n(n \le 2\cdot 10^7)n(n≤2⋅107).

Output

For each test case, print the answer \sum_{i = 1}^n f(i)∑i=1nf(i).

Hint

\sum_{i = 1}^8 f(i)=f(1)+ \cdots +f(8)∑i=18f(i)=f(1)+⋯+f(8)
=1+2+2+1+2+4+2+0=14=1+2+2+1+2+4+2+0=14.

样例输入复制

样例输出复制

8

14

题目来源

ACM-ICPC 2018 南京赛区网络预赛

这个题还是比较难的，但是其实就是一个筛法的改变，只要一个数它出现的次数是2，就是0

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

const int N=2e7+;

bool pri[N];

int prime[N];

ll f[N];

int tot=;

int main()

{

    pri[]=,f[]=;

    for(int i=; i<N; i++)

    {

        if(pri[i]==)prime[tot++]=i,f[i]=;

        for(int j=,num; j<tot&&i*1LL*prime[j]<N; ++j)

        {

            num=i*prime[j],pri[num]=;

            if(i%prime[j])f[num]=f[i]*;

            else if(i%(1LL*prime[j]*prime[j])==)f[num]=;

            else

            {

                f[num]=f[num/prime[j]/prime[j]];

                break;

            }

        }

    }

    for(int i=; i<N; i++)f[i]+=f[i-];

    int t,n;

    scanf("%d",&t);

    while(t--)scanf("%d",&n),printf("%lld\n",f[n]);

}

但是这个可以整除分块

这个做法是sqrt(n)的

#include<stdio.h>

#include<bits/stdc++.h>

using namespace std;

#define lson l,(l+r)/2,rt<<1

#define rson (l+r)/2+1,r,rt<<1|1

#define dbg(x) cout<<#x<<" = "<< (x)<< endl

#define pb push_back

#define fi first

#define se second

#define ll long long

#define sz(x) (int)(x).size()

#define pll pair<long long,long long>

#define pii pair<int,int>

#define pq priority_queue

const int N=2e7+,MD=1e9+,INF=0x3f3f3f3f;

const ll LL_INF=0x3f3f3f3f3f3f3f3f;

const double eps=1e-,e=exp(),PI=acos(-.);

int a[N];

int main()

{

    ios::sync_with_stdio(false),cin.tie(),cout.tie();

    for(int i=; i*i<N; i++)

        for(int j=i*i; j<N; j+=i*i)a[j]=;

    for(int i=; i<N; i++)a[i]+=a[i-];

    int T;

    cin>>T;

    while(T--)

    {

        int n;

        cin>>n;

        ll ans=;

        int l=,r;

        while(l<=n)

        {

            r=n/(n/l)+;

            ans+=1LL*(r-l)*(n/l)-2LL*(a[r-]-a[l-])*(n/l)+1LL*(a[r-]-a[l-])*a[n/l];

            l=r;

        }

        cout<<ans<<"\n";

    }

    return ;

}

Magical Girl Haze

There are NN cities in the country, and MMdirectional roads from uu to v(1\le u, v\le n)v(1≤u,v≤n). Every road has a distance c_ici. Haze is a Magical Girl that lives in City 11, she can choose no more than KK roads and make their distances become 00. Now she wants to go to City NN, please help her calculate the minimum distance.

Input

The first line has one integer T(1 \le T\le 5)T(1≤T≤5), then following TT cases.

For each test case, the first line has three integers N, MN,M and KK.

Then the following MM lines each line has three integers, describe a road, U_i, V_i, C_iUi,Vi,Ci. There might be multiple edges between uu and vv.

It is guaranteed that N \le 100000, M \le 200000, K \le 10N≤100000,M≤200000,K≤10,
0 \le C_i \le 1e90≤Ci≤1e9. There is at least one path between City 11 and City NN.

Output

For each test case, print the minimum distance.

样例输入复制

样例输出复制

题目来源

ACM-ICPC 2018 南京赛区网络预赛

分层最短路

#include<bits/stdc++.h>

using namespace std;

#define ll long long

const int maxn=1e5+,maxm=2e5+;

ll d[][maxn];

int n,m,k;

int head[maxn],cnt;

struct edge

{

    int v,next;

    ll w;

}edges[maxm];

struct node

{

    ll w;

    int v;

    bool operator<(const node &D)const{

        return w>D.w;

    }

};

inline bool read(int &num)

{

        char in;bool IsN=false;

        in=getchar();

        if(in==EOF) return false;

        while(in!='-'&&(in<''||in>'')) in=getchar();

        if(in=='-')

        {

            IsN=true;

            num=;

        }

        else num=in-'';

        while(in=getchar(),in>=''&&in<='')

        {

                num*=,num+=in-'';

        }

        if(IsN) num=-num;

        return true;

}

void dij()

{

    memset(d,0x3f,sizeof d);

    priority_queue<node>q;

    q.push({,});

    d[][]=;

    while(!q.empty())

    {

        auto u=q.top();q.pop();

        if(u.v==n)return;

        for(int i=head[u.v];i!=-;i=edges[i].next)

        {

            edge &v=edges[i];

            for(int j=;j<=k;j++)

            {

                if(j>=&&d[j][v.v]>d[j-][u.v])

                    q.push({d[j][v.v]=d[j-][u.v],v.v});

                if(d[j][v.v]>d[j][u.v]+v.w)

                    q.push({d[j][v.v]=d[j][u.v]+v.w,v.v});

            }

        }

    }

}

int main()

{

    int t;

    read(t);

    while(t--)

    {

        memset(head,-,sizeof head);

        cnt=;

        read(n),read(m),read(k);

        for(int i=,u,v,w;i<m;i++)

        {

            read(u);

            read(v);

            read(w);

            edges[cnt].v=v;

            edges[cnt].w=1LL*w;

            edges[cnt].next=head[u];

            head[u]=cnt++;

        }

        dij();

        ll minn=0x3f3f3f3f3f3f3f3f;

        for(int i=;i<=k;i++)

            minn=min(minn,d[i][n]);

        printf("%lld\n",minn);

    }

    return ;

}