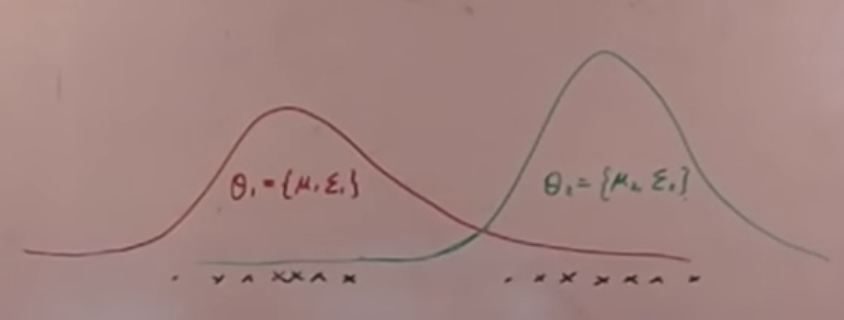
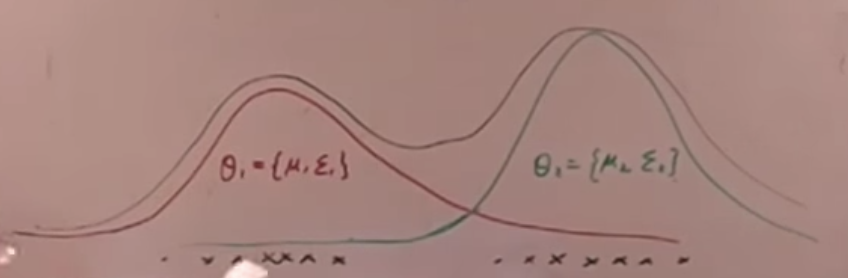
EM算法(徐亦达)笔记


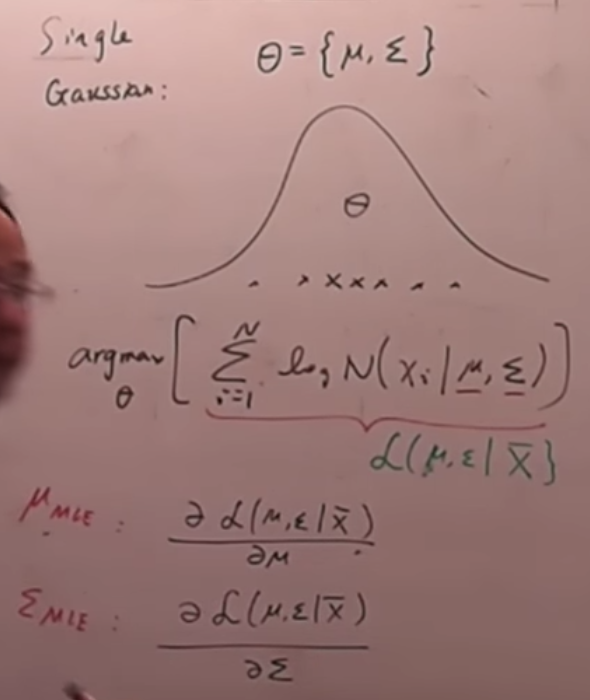



EM算法(徐亦达)笔记的更多相关文章
- EM算法笔记
EM算法在很多地方都用使用到,比如简单的K-means算法,还有在隐马尔可夫里面,也涉及到了EM算法,可见EM算法在机器学习领域的重要地位.在这里就写一下我对于EM算法的一些理解笔记.后续有新的理解也 ...
- 读吴恩达算-EM算法笔记
最近感觉对EM算法有一点遗忘,在表述的时候,还是有一点说不清,于是重新去看了这篇<CS229 Lecture notes>笔记. 于是有了这篇小札. 关于Jensen's inequali ...
- 学习笔记——EM算法
EM算法是一种迭代算法,用于含有隐变量(hidden variable)的概率模型参数的极大似然估计,或极大后验概率估计.EM算法的每次迭代由两步组成:E步,求期望(expectation):M步,求 ...
- 猪猪的机器学习笔记(十四)EM算法
EM算法 作者:樱花猪 摘要: 本文为七月算法(julyedu.com)12月机器学习第十次次课在线笔记.EM算法全称为Expectation Maximization Algorithm,既最大 ...
- GMM高斯混合模型学习笔记(EM算法求解)
提出混合模型主要是为了能更好地近似一些较复杂的样本分布,通过不断添加component个数,能够随意地逼近不论什么连续的概率分布.所以我们觉得不论什么样本分布都能够用混合模型来建模.由于高斯函数具有一 ...
- 《统计学习方法》笔记九 EM算法及其推广
本系列笔记内容参考来源为李航<统计学习方法> EM算法是一种迭代算法,用于含有隐变量的概率模型参数的极大似然估计或极大后验概率估计.迭代由 (1)E步:求期望 (2)M步:求极大 组成,称 ...
- python机器学习笔记:EM算法
EM算法也称期望最大化(Expectation-Maximum,简称EM)算法,它是一个基础算法,是很多机器学习领域的基础,比如隐式马尔科夫算法(HMM),LDA主题模型的变分推断算法等等.本文对于E ...
- 统计学习方法笔记--EM算法--三硬币例子补充
本文,意在说明<统计学习方法>第九章EM算法的三硬币例子,公式(9.5-9.6如何而来) 下面是(公式9.5-9.8)的说明, 本人水平有限,怀着分享学习的态度发表此文,欢迎大家批评,交流 ...
- 《统计学习方法》笔记(9):EM算法和隐马尔科夫模型
EM也称期望极大算法(Expectation Maximization),是一种用来对含有隐含变量的概率模型进行极大似然估计的迭代算法.该算法可应用于隐马尔科夫模型的参数估计. 1.含有隐含参数的概率 ...
随机推荐
- javascript ajax和jquery ajax
一 进行ajax步骤: 1 获取dom值 2发送ajax请求 3返回成功进行前端逻辑处理 二 原生javascript的ajax <!DOCTYPE html> <html> ...
- jquery中attr和prop的区别—判断复选框选中状态
最近项目中需要用jquery判断input里checkbox是否被选中,发现用attr()获取不到复选框改变后的状态,最后查资料发现jQuery 1.6以后新增加了prop()方法,借用官方的一段描述 ...
- 树莓派保持网络连接shell脚本
源:http://www.jianshu.com/p/96aa26d165c3 (我的简书文章) 故事背景 树莓派3b现在有了板载无线网卡,可以很方便的连接到wifi.但是无线路由器不能保证永远正常工 ...
- Android BLE 总结-源码篇(BluetoothLeAdvertiser)
在做Android BLE的应用程序时,我们发出广播数据是调用BluetoothLeAdvertiser的startAdvertising方法,如下所示: mBluetoothLeAdvertiser ...
- Yii的缓存机制之动态缓存
当整个页面被缓存,但只有小部分区域需要根据不同的条件设置不同的信息.(例如商品的详细页面的缓存中用户名是动态的)这里就需要设置动态缓存. 首先在被缓存的模板中使用renderDynamic进行动态渲染 ...
- defaultdict & Counter
在使用python原生的数据结构dict的时候,如果d[key]这样的方式访问,当指定的key不存在时,会抛出keyError异常.但是如果使用defaultdict(导入collections),只 ...
- nvidia-smi 查看GPU信息字段解读
第一栏的Fan:N/A是风扇转速,从0到100%之间变动,这个速度是计算机期望的风扇转速,实际情况下如果风扇堵转,可能打不到显示的转速.有的设备不会返回转速,因为它不依赖风扇冷却而是通过其他外设保持低 ...
- python optparse模块的简单用法
# coding = utf-8 from optparse import OptionParser from optparse import OptionGroup usage = 'Usage: ...
- NOIP2000提高组(RQNOJ314)方格取数
题目描述 设有N*N的方格图(N<=10,我们将其中的某些方格中填入正整数,而其他的方格中则放入数字0.如下图所示(见样例): 某人从图的左上角的A 点出发,可以向下行走,也可以向右走,直到到达 ...
- bzoj4892
后缀数组 先开始nc了,觉得自动机做法是指数级的,就写了个后缀数组 具体方法是暴力,枚举起点,然后用lcp向后暴力匹配,如果失配就减少一次,我们一共有3次机会,这样每次匹配复杂度是O(1)的,所以总复 ...
