激活函数——sigmoid函数（理解）

0 - 定义

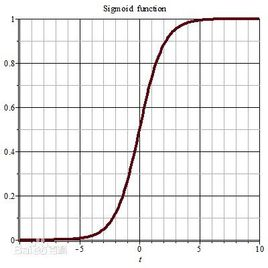
　　$Sigmoid$函数是一个在生物学中常见的S型函数，也称为$S$型生长曲线。在信息科学中，由于其单增以及反函数单增等性质，$Sigmoid$函数常被用作神经网络的阈值函数，将变量映射到0,1之间。

　　其曲线如下图：

　　　　　　　　

1 - 导数

$$\begin{align*}
sigmoid^{'}(x)&=(\frac{1}{1+e^{-x}})^{'} \\
&=\frac{1}{1+e^{-x}}e^{-x}(-1)\\
&=\frac{e^{-x}}{(1+e^{-x})^2}\\
&=\frac{1}{1+e^{-x}}(1-\frac{1}{1+e^{-x}})\\
&=sigmoid(x)(1-sigmoid(x))
\end{align*}$$

2 - 参考资料

https://baike.baidu.com/item/Sigmoid函数/7981407?fr=aladdin