字符串匹配(二)----KMP算法

什么是KMP算法：

　　KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现，因此人们称它为克努特——莫里斯——普拉特操作（简称KMP算法）。KMP算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数，函数本身包含了模式串的局部匹配信息。时间复杂度O(m+n)。

先来看看暴力解法：

　　假设主串是目标字符串为S，模式串是待匹配的字符串为P。用暴力算法匹配字符串过程中，我们会把S[0] 跟 P[0] 匹配，如果相同则匹配下一个字符，直到出现不相同的情况，此时我们会丢弃前面的匹配信息，然后把S[1] 跟 P[0]匹配，循环进行，直到主串结束，或者出现匹配成功的情况。这种丢弃前面的匹配信息的方法，极大地降低了匹配效率。时间复杂度O(m*n)

　　代码：

 /**
      * 暴力解法
      * @param s 主串
      * @param p 模式串
      * @return
      */
     private static int indexOf(String s, String p) {
         int i = 0;
         int sc = i;
         int j = 0;
         while(sc<s.length()){
             if (s.charAt(sc)==p.charAt(j)) {
                 sc++;
                 j++;
                 if (j==p.length()) {
                     return i;
                 }
             }else {
                 i++;
                 sc=i; // 扫描指针以i为起点
                 j=0;  // 恢复为0
             }
         }
         return -1;
     }

　　而在KMP算法中，对于每一个模式串我们会事先计算出模式串的内部匹配信息，在匹配失败时最大的移动模式串，以减少匹配次数。这样主串的指针就不会回溯了，就能保证一次主串的循环就能解决问题。比如，在简单的一次匹配失败后，我们会想将模式串尽量的右移和主串进行匹配。右移的距离在KMP算法中是如此计算的：在已经匹配的模式串子串中，找出最长的相同的前缀和后缀，然后移动使它们重叠

　　

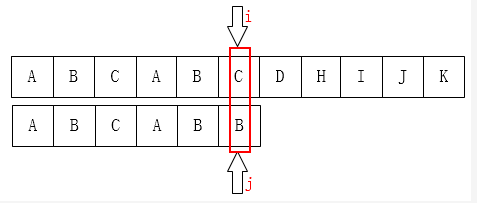
　　这里可以看出指针指向的地方匹配失败，而在已经匹配的模式串子串"ABCAB"中，最长的相同的前缀和后缀是"AB"，长度为2，所以j要向右移动到位置2，因为有相同的前缀和后缀，那么在移动的过程中，这几个字符肯定是能够匹配成功的，就不用去比较了。由此可以得出结论：当匹配失败时，在已经匹配的模式串子串中，如果最前面的k个字符和j之前的最后k个字符是一样的，那么j要移动到下一个位置k。

　　

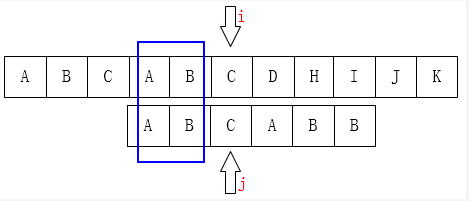
　　然而，如果每次都要计算最长的相同的前缀反而会浪费时间，所以对于模式串来说，我们会提前计算出每个匹配失败的位置应该移动的距离，花费的时间就成了常数时间。因为在P的每一个位置都可能发生不匹配，也就是说我们要计算每一个位置j对应的k，所以用一个数组next来保存，next[j] = k，表示当S[i] != P[j]时，j指针的下一个位置k。那到底怎么计算next数组呢？

　　当j为0时，如果这时候不匹配，这种情况，j已经在最左边了，不可能再移动了，next[0] = -1；那么当j为1的时候，如果不匹配，j指针一定是后移到0位置的，因为它前面也就只有这一个位置了，next[1] = 0;如果p[j]==p[k]或者k<0,next[++j] = ++k，否则，k=next[k]。

　　

　　代码：

   public static int[] next(String ps) {
     int pLength = ps.length();
     int[] next = new int[pLength + 1];
     char[] p = ps.toCharArray();
     next[0] = -1;
     if (ps.length() == 1)
       return next;
     next[1] = 0;

     int j = 1;
     int k = next[j]; //看看位置j的最长匹配前缀在哪里

     while (j < pLength) {
       //现在要推出next[j+1],检查j和k位置上的关系即可
       if (k < 0 || p[j] == p[k]) {
         next[++j] = ++k;
       } else {
         k = next[k];
       }
     }
     return next;
   }

　　那么完整的代码就是：

public class KMP {

    public static void main(String[] args) {
        String src = "babababcbabababb";
        int index = indexOf(src, "bababb");
        System.out.println("暴力破解法："+index);
        index = indexOf1(src, "bababb");
        System.out.println("KMP算法："+index);
    }

    //O(m+n),求count 总共出现了多少次
    private static int indexOf1(String s, String p) {
        if (s.length()==0||p.length()==0) {
            return -1;
        }
        if (p.length()>s.length()) {
            return -1;
        }

//        int count = 0;
        int []next = next(p);
        int i = 0;//s位置
        int j = 0;//p位置
        int sLen = s.length();
        int pLen = p.length();

        while(i<sLen){
            // ①如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++
            // j=-1，因为next[0]=-1,说明p的第一位和i这个位置无法匹配，这时i，j都增加1，i移位，j从0开始
            if (j == -1 || s.charAt(i) == p.charAt(j)) {
                i++;
                j++;
            } else {
                // ②如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]
                // next[j]即为j所对应的next值
                j = next[j];
            }
            if (j == pLen) {// 匹配成功了
//                count++;
//                j = next[j];
                // 上面两行代码是计数模式字符串总共出现了多少次的
                return (i - j);
            }
        }
        return -1;
//        return count; // -1
    }

    public static int[] next(String ps){
        int pLength = ps.length();
        int []next = new int[pLength+1];
        char []p = ps.toCharArray();
        next[0] = -1;
        if (ps.length()==1) {
            return next;
        }
        next[1] = 0;

        int j = 1;
        int k = next[j];  // 看看位置j的最长匹配前缀在哪里

        while(j<pLength){
            // 现在要推出next[j+1],检查j和k位置上的关系即可
            if (k<0||p[j]==p[k]) {
                next[++j] = ++k;
            }else {
                k = next[k];
            }
        }
        return next;
    }
    /**
     * 暴力解法
     * @param s 主串
     * @param p 模式串
     * @return
     */
    private static int indexOf(String s, String p) {
        int i = 0;
        int sc = i;
        int j = 0;
        while(sc<s.length()){
            if (s.charAt(sc)==p.charAt(j)) {
                sc++;
                j++;
                if (j==p.length()) {
                    return i;
                }
            }else {
                i++;
                sc=i; // 扫描指针以i为起点
                j=0;  // 恢复为0
            }
        }
        return -1;
    }

}

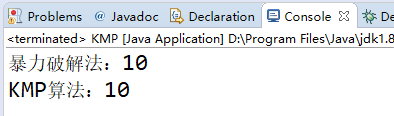
　　结果：