python实现树结构

树在计算机科学的许多领域中使用，包括操作系统，图形，数据库系统和计算机网络。树数据结构与他们的植物表亲有许多共同之处。树数据结构具有根，分支和叶。自然界中的树和计算机科学中的树之间的区别在于树数据结构的根在顶部，其叶在底部。

1 树的相关定义

节点：树的基本部分。它可以有一个名称，我们称之为“键”。节点也可以有附加信息。我们将这个附加信息称为“有效载荷”。虽然有效载荷信息不是许多树算法的核心，但在利用树的应用中通常是关键的。

边：树的另一个基本部分。边连接两个节点以显示它们之间存在关系。每个节点（除根之外）都恰好从另一个节点的传入连接。每个节点可以具有多个输出边。

根：树的根是树中唯一没有传入边的节点。

路径：路径是由边连接节点的有序列表。

子节点：具有来自相同传入边的节点 c 的集合称为该节点的子节点。

父节点：具有和它相同传入边的所连接的节点称为父节点。

兄弟节点：树中作为同一父节点的子节点的节点被称为兄弟节点。

子树：由父节点和该父节点的所有后代组成的一组节点和边。

叶节点：叶节点是没有子节点的节点。

高度：树的高度等于树中任何节点的最大层数。

定义一：树由一组节点和一组连接节点的边组成。树具有以下属性：

• 树的一个节点被指定为根节点。
• 除了根节点之外，每个节点 n 通过一个其他节点 p 的边连接，其中 p 是 n 的父节点。
• 从根路径遍历到每个节点路径唯一。
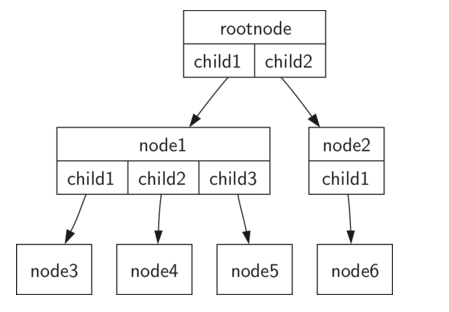
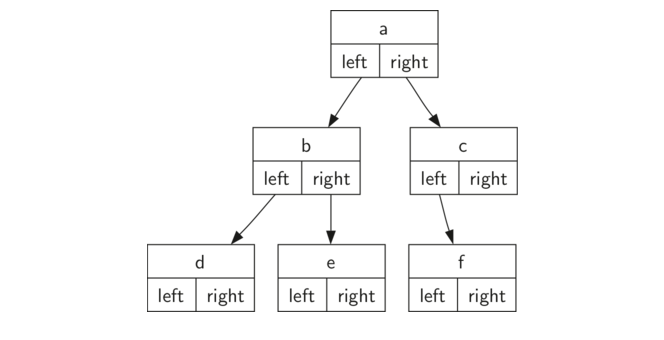
• 如果树中的每个节点最多有两个子节点，我们说该树是一个二叉树。下图展示了合适定义一的。

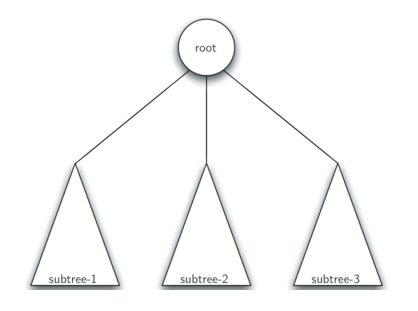
定义二：树是空的，或者由一个根节点和零个或多个子树组成，每个子树也是一棵树。每个子树的根节点通过边连接到父树的根节点。 下图 说明了树的这种递归定义。使用树的递归定义，我们知道 下图中的树至少有四个节点，因为表示一个子树的每个三角形必须有一个根节点。 它可能有比这更多的节点，但我们不知道，除非我们更深入树。

2 列表表示树结构

2.1 结构示意图

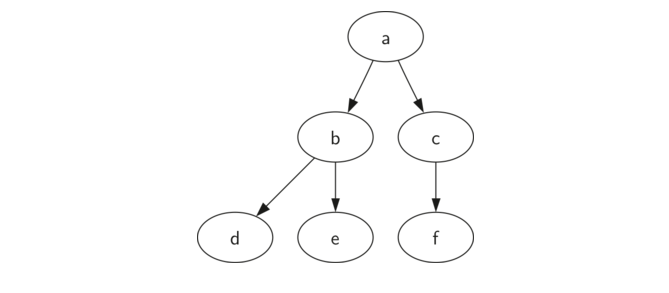
列表为我们提供了一个简单的递归数据结构，我们可以直接查看和检查。在列表树的列表中，我们将根节点的值存储为列表的第一个元素。列表的第二个元素本身将是一个表示左子树的列表。列表的第三个元素将是表示右子树的另一个列表。下图展示了一个简单的树和相应的列表实现。

myTree = ['a',   #root
      ['b',  #left subtree
       ['d', [], []],
       ['e', [], []] ],
      ['c',  #right subtree
       ['f', [], []],
       [] ]
     ]

树的根是 myTree[0]，根的左子树是 myTree[1]，右子树是 myTree[2]

2.2 数的函数表达

下面我们用列表作为树的函数来形式化树数据结构的定义（并非定义一个二叉树类），帮助我们操纵一个标准列表。

def BinaryTree(r):
    return [r, [], []]

BinaryTree 函数简单地构造一个具有根节点和两个子列表为空的列表。

2.3 插入子节点

要将左子树添加到树的根，我们需要在根列表的第二个位置插入一个新的列表。我们必须小心。如果列表已经在第二个位置有东西，我们需要跟踪它，并沿着树向下把它作为我们添加的列表的左子节点。下面代码展示了插图左子节点和右子节点的 python 代码。

def insertLeft(root,newBranch):
    t = root.pop(1)
    if len(t) > 1:
        root.insert(1,[newBranch,t,[]])
    else:
        root.insert(1,[newBranch, [], []])
    return root

def insertRight(root,newBranch):
    t = root.pop(2)
    if len(t) > 1:
        root.insert(2,[newBranch,[],t])
    else:
        root.insert(2,[newBranch,[],[]])
    return root

要插入一个左子节点，我们首先获得与当前左子节点对应的（可能为空的）列表。然后我们添加新的左子树，添加旧的左子数作为新子节点的左子节点。这允许我们在任何位置将新节点拼接到树中。

下面编写一些访问函数来获取和设置根节点的值，以及获取左或右子树，完成这组树形函数。

def getRootVal(root):
    return root[0]

def setRootVal(root,newVal):
    root[0] = newVal

def getLeftChild(root):
    return root[1]

def getRightChild(root):
    return root[2]

3 节点表示

3.1 结构示意图

示意图第二种表示树的方法使用节点和引用。在这种情况下，我们将定义一个具有根值属性的类，以及左和右子树。 它的结构类似于下图：

3.2 构造类

这个表示重要的事情是 left和 right 的属性将成为对 BinaryTree 类的其他实例的引用。 例如，当我们在树中插入一个新的左子节点时，我们用 python 创建另一个 BinaryTree 实例如下，并在根节点中修改self.leftChild 来引用新树节点。

class BinaryTree:
    def __init__(self,rootObj):
        self.key = rootObj
        self.leftChild = None
        self.rightChild = None

构造函数希望获取某种对象存储在根中。 就像你可以在列表中存储任何你喜欢的对象一样，树的根对象可以是对任何对象的引用。 对于我们的先前示例，我们将存储节点的名称作为根值。使用节点和引用来表示 Figure 2 中的树，我们将创建 BinaryTree 类的六个实例。

3.2.1 添加节点

要向树中添加一个左子树，我们将创建一个新的二叉树对象，并设置根的左边属性来引用这个新对象。 代码如下：

def insertLeft(self,newNode):
    if self.leftChild == None:
        self.leftChild = BinaryTree(newNode)
    else:
        t = BinaryTree(newNode)
        t.leftChild = self.leftChild
        self.leftChild = t

我们必须考虑两种插入情况。 第一种情况的特征没有现有左孩子的节点。当没有左子代时，只需向树中添加一个节点。 第二种情况的特征在于具有现有左子代的节点。在第二种情况下，我们插入一个节点并将现有的子节点放到树中的下一个层。第二种情况由 Listing 5 第 4 行的 else 语句处理。同理，在根和现有的右子代之间插入节点。

def insertRight(self,newNode):
    if self.rightChild == None:
        self.rightChild = BinaryTree(newNode)
    else:
        t = BinaryTree(newNode)
        t.rightChild = self.rightChild
        self.rightChild = t

3.2.2 获取左右子代和根植

def getRightChild(self):
    return self.rightChild

def getLeftChild(self):
    return self.leftChild

def setRootVal(self,obj):
    self.key = obj

def getRootVal(self):
    return self.key

3 完整的二叉树结构

使用节点 a 作为根的简单树，并将节点 b 和 c 添加为子节点。下面代码创建树并查看存储在 key，left 和 right 中的一些值。

class BinaryTree:
    def __init__(self,rootObj):
        self.key = rootObj
        self.leftChild = None
        self.rightChild = None

    def insertLeft(self,newNode):
        if self.leftChild == None:
            self.leftChild = BinaryTree(newNode)
        else:
            t = BinaryTree(newNode)
            t.leftChild = self.leftChild
            self.leftChild = t

    def insertRight(self,newNode):
        if self.rightChild == None:
            self.rightChild = BinaryTree(newNode)
        else:
            t = BinaryTree(newNode)
            t.rightChild = self.rightChild
            self.rightChild = t

    def getRightChild(self):
        return self.rightChild

    def getLeftChild(self):
        return self.leftChild

    def setRootVal(self,obj):
        self.key = obj

    def getRootVal(self):
        return self.key

r = BinaryTree('a')
print(r.getRootVal())
print(r.getLeftChild())
r.insertLeft('b')
print(r.getLeftChild())
print(r.getLeftChild().getRootVal())
r.insertRight('c')
print(r.getRightChild())
print(r.getRightChild().getRootVal())
r.getRightChild().setRootVal('hello')
print(r.getRightChild().getRootVal())

参考资料：《problem-solving-with-algorithms-and-data-structure-using-python》 
http://www.pythonworks.org/pythonds