对于约束优化问题：

拉格朗日公式：

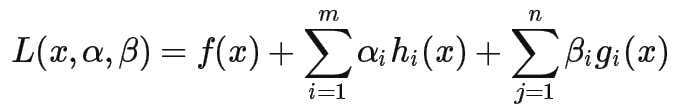
其KKT条件为：

求解 x、α、β

其中β*g(x)为互补松弛条件

KKT条件是使一组解成为最优解的必要条件，当原问题是凸问题的时候，KKT条件也是充分条件。

最优化 KKT条件的更多相关文章

  1. 机器学习——支持向量机(SVM)之拉格朗日乘子法，KKT条件以及简化版SMO算法分析

    SVM有很多实现,现在只关注其中最流行的一种实现,即序列最小优化(Sequential Minimal Optimization,SMO)算法,然后介绍如何使用一种核函数(kernel)的方式将SVM ...

  2. 【整理】深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT条件

    在求解最优化问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法.在有等式约束时使用拉格朗日乘子法,在有不等约束时使用 ...

  3. 深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT条件

    [整理]   在求解最优化问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法.在有等式约束时使用拉格朗日乘子法,在有 ...

  4. 装载：关于拉格朗日乘子法与KKT条件

    作者:@wzyer 拉格朗日乘子法无疑是最优化理论中最重要的一个方法.但是现在网上并没有很好的完整介绍整个方法的文章.我这里尝试详细介绍一下这方面的有关问题,插入自己的一些理解,希望能够对大家有帮助. ...

  5. 寻找“最好”（4）——不等约束和KKT条件

    不等约束 上篇文章介绍了如何在等式约束下使用拉格朗日乘子法,然而真实的世界哪有那么多等式约束?我们碰到的大多数问题都是不等约束.对于不等约束的优化问题,可以这样描述: 其中f(x)是目标函数,g(x) ...

  6. 关于拉格朗日乘子法与KKT条件

    关于拉格朗日乘子法与KKT条件 关于拉格朗日乘子法与KKT条件   目录 拉格朗日乘子法的数学基础 共轭函数 拉格朗日函数 拉格朗日对偶函数 目标函数最优值的下界 拉格朗日对偶函数与共轭函数的联系 拉 ...

  7. KKT条件和拉格朗日乘子法详解

    \(\frac{以梦为马}{晨凫追风}\) 最优化问题的最优性条件,最优化问题的解的必要条件和充分条件 无约束问题的解的必要条件 \(f(x)\)在\(x\)处的梯度向量是0 有约束问题的最优性条件 ...

  8. ML-对偶(Duality)问题 KKT 条件

    Primal => Dual 现实中我们遇到的原优化问题, 写为标准型的话是这样的. \(min _w f(w) \\ s.t. \\ g_i(w) <=0 \\ h_i(w) = 0\) ...

  9. 机器学习——最优化问题：拉格朗日乘子法、KKT条件以及对偶问题

    1 前言 拉格朗日乘子法(Lagrange Multiplier)  和 KKT(Karush-Kuhn-Tucker)  条件是求解约束优化问题的重要方法,在有等式约束时使用拉格朗日乘子法,在有不等 ...

随机推荐

  1. orcale 之sql/plus set 命令

    set 命令用于设置系统变量的值.通过set 命令设置的系统变量有很多,下面把最常用的罗列出来: 1. arraysize 用于从数据库中一次提取的行数,其默认为 15. SQL> show a ...

  2. WPF中使用Grid来实现图层的效果

    <Style x:Key="ScanButtonStyle" TargetType="{x:Type Button}"> <!--<Se ...

  3. C#控件的Resize事件

    1. 当控件大小发生改变时,就会触发该事件 所以适合动态调整UI的布局, 例如: 国际化,不同语言导致控件长度不同: 控件的内容是动态增加的,也可以使用. 2.必须是大小会发生改变的控件才会触发该事件 ...

  4. tar.gz和bin，以及rpm，deb等linux后缀的文件的区别

    先说tar.gz源码类的吧.这种要你手动安装,编译,首先你还要安装了相关的编译软件如gcc g++ 等.一般操作 configure , make && make install. 其 ...

  5. bzoj 4561: [JLoi2016]圆的异或并

    Description 在平面直角坐标系中给定N个圆.已知这些圆两两没有交点,即两圆的关系只存在相离和包含.求这些圆的异或面 积并.异或面积并为:当一片区域在奇数个圆内则计算其面积,当一片区域在偶数个 ...

  6. [转]Android Studio SQLite Database Multiple Tables Example

    本文转自:http://instinctcoder.com/android-studio-sqlite-database-multiple-tables-example/ BY TAN WOON HO ...

  7. SQL SERVER学习2——数据库设计

    数据库设计是数据库知识中比较重要的部分,我们需要了解数据库设计的基本步骤,E-R图的画法. 数据库设计的基本概述 检验一个数据库设计好坏的标准就是,看他是否能够方便的执行各种数据检索和处理操作,并且有 ...

  8. JavaScript中自定义函数以及文本框、radio、下拉框的值的获取，结合淘宝竞拍案例来理解。。。

    淘宝竞拍案例: HTML部分代码: <form action="#" method="post"> <h2>欢迎进入淘宝竞拍</h ...

  9. Redis实现分布式锁1

    Jedis结合setNX方法实现分布式锁 public boolean lock(String key, int exprie) { try { exprie = exprie <= 0 ? 6 ...

  10. TopCoder14580: EllysRPS

    题意 \(yyb\)要去与\(m\)\((m\le100)\)个人玩游戏 由于\(yyb\)忙着切大火题,他没有太多的精力浪费在游戏上 所以仁慈的\(yyb\)决定放\(m\)个人一条生路,不吊打他们 ...