POJ2369 Permutations（置换的周期）

链接：http://poj.org/problem?id=2369

Permutations

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 3039		Accepted: 1639

Description

We remind that the permutation of some final set is a one-to-one mapping of the set onto itself. Less formally, that is a way to reorder elements of the set. For example, one can define a permutation of the set {1,2,3,4,5} as follows: 
 
This record defines a permutation P as follows: P(1) = 4, P(2) = 1, P(3) = 5, etc. 
What is the value of the expression P(P(1))? It’s clear, that P(P(1)) = P(4) = 2. And P(P(3)) = P(5) = 3. One can easily see that if P(n) is a permutation then P(P(n)) is a permutation as well. In our example (believe us) 
 
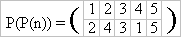
It is natural to denote this permutation by P2(n) = P(P(n)). In a general form the defenition is as follows: P(n) = P1(n), Pk(n) = P(Pk-1(n)). Among the permutations there is a very important one — that moves nothing: 
 
It is clear that for every k the following relation is satisfied: (EN)k = EN. The following less trivial statement is correct (we won't prove it here, you may prove it yourself incidentally): Let P(n) be some permutation of an N elements set. Then there exists a natural number k, that Pk = EN. The least natural k such that Pk = EN is called an order of the permutation P. 
The problem that your program should solve is formulated now in a very simple manner: "Given a permutation find its order."

Input

In the first line of the standard input an only natural number N (1 <= N <= 1000) is contained, that is a number of elements in the set that is rearranged by this permutation. In the second line there are N natural numbers of the range from 1 up to N, separated by a space, that define a permutation — the numbers P(1), P(2),…, P(N).

Output

You should write an only natural number to the standard output, that is an order of the permutation. You may consider that an answer shouldn't exceed 10⁹.

Sample Input

5
4 1 5 2 3

Sample Output

6

置换的周期是轮换长度的最小公倍数

代码：

#include <iostream>
#include <stdio.h>
#include <string.h>
using namespace std;
#define MAXN 1005
long long lcm(long long a,long long b)
{
    long long temp;
    long long a0,b0;
    a0=a;
    b0=b;
    while(b)
    {
        temp=b;
        b=a%b;
        a=temp;
    }
    return a0/a*b0;
}
int main()
{
    int n;
    int i,j;
    long long p[MAXN];
    long long g[MAXN];
    int cnt;
    long long l;
    bool flag[MAXN];
    memset(flag,false,sizeof(flag));
    scanf("%d",&n);
    for(i=;i<=n;i++)
        scanf("%I64d",&p[i]);
    cnt=;
    for(i=;i<=n;i++)
    {
        if(flag[i])
            continue;
        g[cnt]=;
        j=i;
        while(p[j]!=i)
        {
            flag[j]=true;
            j=p[j];
            g[cnt]++;
        }
        cnt++;
    }
    l=g[];
    for(i=;i<cnt;i++)
    {
        l=lcm(l,g[i]);
    }
    printf("%I64d\n",l);
    return ;
}