【luogu P3901 数列找不同】 题解

对于区间查询的问题，提供一种思路：

莫队。

莫队是处理区间问题的乱搞神器，尤其是对于离线查询问题，当然也可以做在线查询，比如带修莫队。

对于有的题，莫队是乱搞骗分，而在某些地方，莫队是正解。

这道题来说，可以当做是萌新初学莫队的一个板子，而且莫队也好理

解。线段树树状数组这类也可以做，但是相比莫队而言麻烦些。（个

人见解，不喜勿喷。谢谢）

---

1st.关于莫队的思想:

先明白一点，莫队可以理解成：

优雅的暴力。

暴力算法几乎人人都会，所以莫队理解起来好理解。

如果让你暴力的话呢？

我们用一个cnt[ ]数组记录每种元素，用桶排的思想，枚举区间，每遇到一个元素对应的桶++，然后暴力一遍所有的桶，等于1的我们ans就++，这样统计不同的个数，看看是不是等于L到R，然后再清空桶和ans，做下一组询问。

对于一般的暴力算法往往会TLE，那么莫队是怎么做的呢？

首先：考虑我们有两个指针。一个叫做curL，另一个叫curR。他们对应的是所指的数的标号。这样我们可以利用这两个指针进行移动，每次只能向左或向右移动一步。移动的复杂度是O(1)。

eg：

我们现在处理了curL—curR区间内的数据，现在左右移动，比如curL到curL-1，只需要更新上一个新的3，即curL-1。

那么curL到curL+1，我们只需要去除掉当前curL的值。因为curL+1是已经维护好了的。

curR同理，但是要注意方向哦！curR到curR+1是更新，curR到cur-1是去除。

我们先计算一个区间 [curL curR] 的answer，这样的话，我们就可以用O(1)转移到 [curL-1 curR] [curL+1 curR] [curL curR+1] [curL curR-1] 上来并且求出这些区间的answer。

我们利用curL和curR，就可以移动到我们所需要求的[L R]上啦~

这样做会快很多，但是......

如果有个**数据，让你在每个L和R间来回跑，而且跨度很大呢？？

我们每次只动一步，岂不是又T了？？

但是这其实就是莫队算法的核心了。我们的莫队算法还有优化。

这就是莫队算法最精明的地方（我认为的qwq）

我们想，因为每次查询是离线的，所以我们先给每次的查询排一个序。

排序的方法是

分块。

我们把所有的元素分成多个块（即分块）。分了块跑的会更快。再按照右端点从小到大，左端点块编号相同按右端点从小到大。

为什么要这么排序呢？

如果不是按照分块排序，那么一种直观的办法是按照左端点排序，再按照右端点排序。但是这样的表现不好。特别是面对精心设计的数据，这样方法表现得很差。

举个栗子，有6个询问如下：(1, 100), (2, 2), (3, 99), (4, 4), (5, 102), (6, 7)。

这个数据已经按照左端点排序了。用上述方法处理时，左端点会移动6次，右端点会移动移动98+97+95+98+95=483次。

其实我们稍微改变一下询问处理的顺序就能做得更好：(2, 2), (4, 4), (6, 7), (5, 102), (3, 99), (1, 100)。

左端点移动次数为2+2+1+2+2=9次，比原来稍多。右端点移动次数为2+3+95+3+1=104，右端点的移动次数大大降低了。

上面的过程启发我们：我们不应该严格按照升序排序，而是根据需要灵活一点的排序方法

这样，不断地移动端点指针+精妙的排序，就是普通莫队的思想啦~

---

2ec.Code

1.对于每组查询的记录和排序：

l，r为左右区间编号，p是第几组查询的编号（记录下来为了排序后不打乱顺序还按照原查询的顺序输出），bl是分块数。

struct query{
    int l, r, p;
}e[maxn];

bool cmp(query a, query b)
{
    return (a.l/bl) == (b.l/bl) ? a.r < b.r : a.l < b.l;
}

2.处理和初始变量：

answer就是所求答案， bl是分块数量， a[]是原序列， ans[]是记录原查询序列下的答案， cnt[]是记录对于每个数i， cnt[i]表示i出现过的次数， curL和curR不再解释， nm看题意要求。 add和del每个题有不同的写法。

int answer, a[maxn], m, n, bl, ans[maxn], cnt[maxn], k, curL = 1, curR = 0;
void add(int pos)//添加
{
    //do sth...
}
void del(int pos)//去除
{
    //do sth...
}
//一般写法都是边处理 边根据处理求答案。cnt[a[pos]]就是在pos位置上原序列a出现的次数。

3.主体部分及输出：

预处理查询编号，用四个while移动指针顺便处理。

在这里着重说下四个while

我们设想有一条数轴:

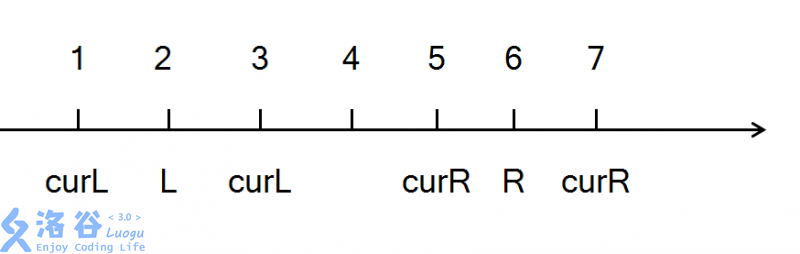
当curL < L 时，我们当前curL是已经处理好的了。所以del时先去除当前curL再++

当curL > L 时，我们当前curL是已经处理好的了。所以 add 时先 -- 再加上改后的curL

当curR > R 时，我们当前curR是已经处理好的了。所以del时先去除当前curR再 --

当curR < R 时，我们当前curR是已经处理好的了。所以 add 时先++再加上改后的curR

n = read(); m = read(); k = read();
    bl = sqrt(n);

    for(int i = 1; i <= n; i++)
    a[i] = read();

    for(int i = 1; i <= m; i++)
    {
        e[i].l = read(); e[i].r = read();
        e[i].p = i;
    }

    sort(e+1,e+1+m,cmp);

    for(int i = 1; i <= m; i++)
    {
        int L = e[i].l, R = e[i].r;
        while(curL < L)
        del(curL++);
        while(curL > L)
        add(--curL);
        while(curR > R)
        del(curR--);
        while(curR < R)
        add(++curR);
        ans[e[i].p] = answer;
    }
    for(int i = 1; i <= m; i++)
    printf("%d\n",ans[i]);
    return 0;

---

3th.关于这题题解

我的想法还是蛮暴力的，对于出现过的数直接记录下来，answer记录出现了多少个不同的数，如果answer等于现在的R-L+1，那么说明出现的数与L到R相同。

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
#define ri register
using namespace std;
const int maxn = 100010;
inline int read()
{
    int k=0;
    char c;
    c=getchar();
    while(!isdigit(c))c=getchar();
    while(isdigit(c)){k=(k<<3)+(k<<1)+c-'0';c=getchar();}
    return k;
}
int n, m, bl, answer = 0, curL, curR, cnt[maxn], a[maxn];
bool ans[maxn];
struct Query{
    int l, r, p;
}q[maxn];
bool cmp(const Query &a, const Query &b)
{
    return (a.l/bl) == (b.l/bl) ? a.r < b.r : a.l < b.l;
}
void add(int pos)
{
    if((++cnt[a[pos]]) == 1) ++answer;
}
void del(int pos)
{
    if((--cnt[a[pos]]) == 0) --answer;
}
int main()
{
    n = read();
    m = read();
    bl = sqrt(n);
    for(ri int i = 1; i <= n; i++)
    a[i] = read();

    for(ri int i = 1; i <= m; i++)
    {
        q[i].l = read();
        q[i].r = read();
        q[i].p = i;
    }

    sort(q+1,q+1+m,cmp);

    for(ri int i = 1; i <= m; i++)
    {
        int L = q[i].l, R = q[i].r;
        while(curL < L) del(curL++);
        while(curL > L) add(--curL);
        while(curR < R) add(++curR);
        while(curR > R) del(curR--);
        if(answer == (R-L+1))
        ans[q[i].p] = 1;
    }
    for(ri int i = 1; i <= m; i++)
    {
        if(ans[i] == 1)
        printf("Yes\n");
        else
        printf("No\n");
    }
    return 0;
}

---

如果对于莫队算法有什么疑问或者对我的题解有什么建议欢迎和我讨论，本人会尽力解答和虚心接受意见的。