hdu6158（圆的反演）

hdu6158

题意

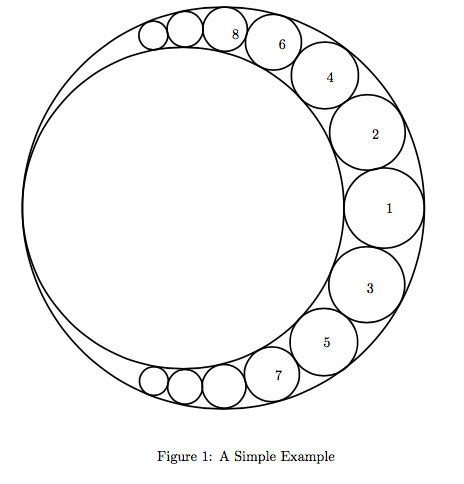
初始有两个圆，按照标号去放圆，问放完 \(n\) 个圆后的总面积。

分析

圆的反演的应用。

参考blog

设反演圆心为 \(O\) 和反演半径 \(R\)

圆的反演的定义：

已知一圆 \(C\) ，圆心为 \(O\) ，半径为 \(R\) ，如果 \(P\) 与 \(P'\)在过圆心 \(O\) 的直线上且 \(OP \cdot OP'=R^2\)，则称 \(P\) 与 \(P'\) 关于 \(O\) 互为反演点。

有圆的反演的几个性质：

1. 经过\(O\)的圆，反演后成为不经过\(O\)的一条直线
2. 不经过\(O\)的圆，反演后成为另一个圆，且圆心并不对应
3. 不经过\(O\)的直线反演后成为一个经过\(O\)的圆
4. 过 \(O\)的直线反演后不变

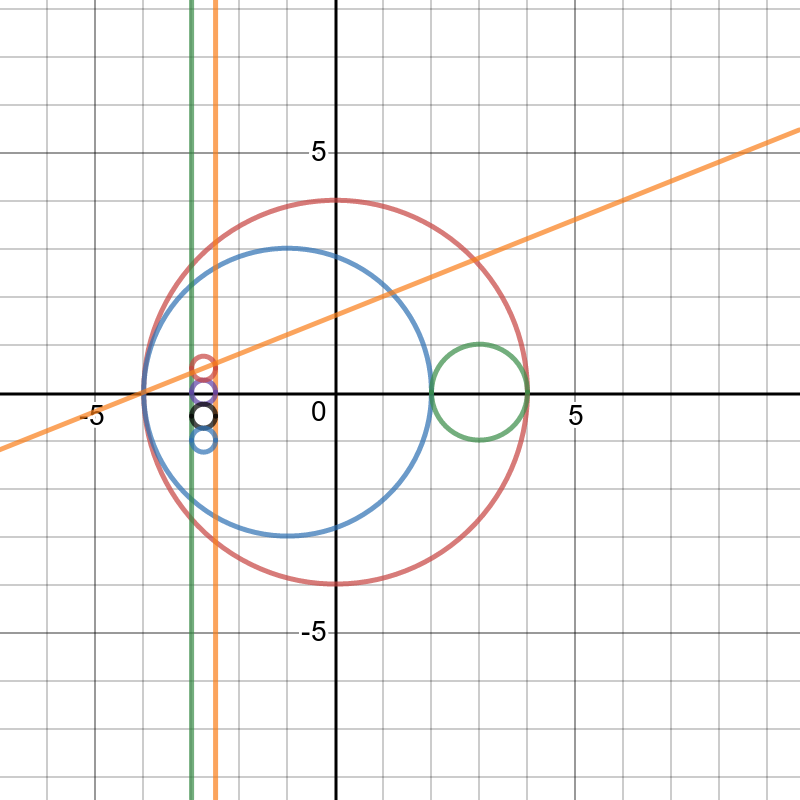
以 \((-4, 0)\) 为反演圆心，选取某一半径。（ 上图数据并不准确，只是大致反应图形间的关系 ）

那么将要填充的所有圆反演之后就变成了两条直线间具有相同半径的小圆，其中左边的直线为外面的大圆反演而来，右边的直线为里面的大圆反演而来。

小圆的圆心与反演圆心的连线在小圆上的交点，再反演一次得到两个点，它们之间的距离就是原来圆的直径。

code

#include<bits/stdc++.h>
using namespace std;
const double PI = acos(-1);
inline double Sqr(double x) { return x * x; }
int main() {
    int T;
    cin >> T;
    while(T--) {
        double r1, r2;
        int n;
        cin >> r1 >> r2 >> n;
        if(r1 < r2) swap(r1, r2); // r1:大 r2:小
        double x = (1.0 / r2 / 2.0 + 1.0 / r1 / 2.0) / 2.0;
        double r = (1.0 / r2 / 2.0 - 1.0 / r1 / 2.0) / 2.0;
        double ans = PI * (r1 - r2) * (r1 - r2);
        double h = 2 * r;
        for(int i = 1; i <= n / 2; i++) {
            double d = hypot(x, h);
            double res = PI * Sqr((1.0 / (d - r) - 1.0 / (d + r)) / 2.0);
            ans += res;
            if(i * 2 < n) ans += res;
            h += 2.0 * r;
            if(res * (n - 2 * i) < 1e-6) break;
        }
        printf("%.5f\n", ans);
    }
    return 0;
}