HDU6395(分段+矩阵快速幂)

题目：http://acm.hdu.edu.cn/showproblem.php?pid=6395

给你一个式子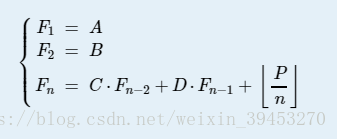，给出你A,B,C,D,P,n，让你求出第n项的式子Fn。（其中ABCDPn均在1e9的范围内）

分析： 如果Fn=C*F(n-2) + D*F(n-1) + num ; 我们就可以直接构造出这个斐波那契的矩阵快速幂 ：写出相似的矩阵

1.f(n)=a*f(n-1)+b*f(n-2)+c；（a,b,c是常数）

但是这里的P/n 是变化的 ， 我们无法转化出来 ， 但是这里 P/n 是向下取整 也 就是说会有一段一段的区间里面的 p/i 是相等的 ； 所以我们现在找到这些一段一段然后用矩阵快速幂

#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
const int mod=1e9+;
typedef long long ll;
struct Marix{
    ll mo[][];
    Marix(){
        memset(mo,,sizeof(mo));
    }
};
Marix mul(Marix a,Marix b){
    Marix c;
    for(int i=;i<;i++){
        for(int j=;j<;j++){
            for(int k=;k<;k++){
                c.mo[i][j]=(c.mo[i][j]+a.mo[i][k]*b.mo[k][j])%mod;
            }
        }
    }
    return c;
}
Marix powmod(Marix a,ll n){//矩阵快速幂模板
    Marix tmp;
    for(int i=;i<;i++){
        tmp.mo[i][i]=;
    }
    while(n){
        if(n&) tmp=mul(tmp,a);
        n>>=;
        a=mul(a,a);
    }
    return tmp;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--){
        ll a,b,c,d,p,n;
        scanf("%lld%lld%lld%lld%lld%lld",&a,&b,&c,&d,&p,&n);
        if(n==){
            printf("%lld\n",a);
            continue;
        }
        if(n==){
            printf("%lld\n",b);
            continue;
        }
        Marix m;
        m.mo[][]=d,m.mo[][]=c,m.mo[][]=,m.mo[][]=;
        bool vis=;
        for(ll i=;i<=n;){
            if(p/i==){//倘若当前项大于p了，则直接用矩阵快速幂求解剩下的项
                Marix tmp;
                tmp=m;
                tmp=powmod(tmp,n-i+);
                ll res=(tmp.mo[][]*b+tmp.mo[][]*a+tmp.mo[][])%mod;
                printf("%lld\n",res);
                vis=;
                break;
            }//否则，不断的分段求解矩阵的值，并将矩阵的值进行修改
            ll j=min(n,p/(p/i));
            Marix tmp;
            tmp=m;
            tmp.mo[][]=p/i;
            tmp=powmod(tmp,j-i+);
            ll A=(tmp.mo[][]*b+tmp.mo[][]*a+tmp.mo[][])%mod;
            ll B=(tmp.mo[][]*b+tmp.mo[][]*a+tmp.mo[][])%mod;
            a=A,b=B;
            i=j+;
        }
        if(!vis) printf("%lld\n",b);
    }
    return ;
}

新感受!

做的时候大概的想法是想到的了 ， 但是无法解决F1=A， F2=B , 的情况  ， 之后看的别人的代码才大悟出来 ；

只要求出最后的答案后，在成系数

fn=mo[0][0]*(f2) + mo[0][1]*(f1) 就好拉

例如

ll ans=(tmp.mo[0][0]*b+tmp.mo[0][1]*a+tmp.mo[0][2])%mod;

参考代码

/*
*  Author: windystreet
*  Date  : 2018-08-14 09:46:10
*  Motto : Think twice, code once.
*/
#include<bits/stdc++.h>

using namespace std;

#define X first
#define Y second
#define eps  1e-5
#define gcd __gcd
#define pb push_back
#define PI acos(-1.0)
#define lowbit(x) (x)&(-x)
#define bug printf("!!!!!\n");
#define mem(x,y) memset(x,y,sizeof(x))

typedef long long LL;
typedef long double LD;
typedef pair<int,int> pii;
typedef unsigned long long uLL;

const int maxn = 1e5+;
const int INF  = <<;
const int mod  = 1e9+;

struct Matrix
{
    int n,m;
    LL ma[][];
    Matrix (int x,int y):n(x),m(y){clear();}
    void set(int n_,int m_){n = n_,m = m_;}
    LL *operator[](int x){return ma[x];}
    Matrix operator*(Matrix x){
        Matrix res(n,x.m);
        for(int i=;i<=n;i++)
            for(int j=;j<=x.m;j++)
                for(int k=;k<=m;k++)
                    (res[i][j]+=ma[i][k]*x[k][j]%mod+mod)%=mod;
        return res;
    }
    Matrix operator ^(int y){
        Matrix x(n,m);
        for(int i=;i<=n;i++)
            for(int j=;j<=m;j++)
                x[i][j]=ma[i][j];
        Matrix res(x.n,x.n);
        for(int i=;i<=x.n;i++)
            res[i][i]=;
        for(;y;y>>=,x=x*x)
            if(y&)res=res*x;
        return res;
    }
    void print(){
        for(int i=;i<=n;i++)
            for(int j=;j<=m;j++)
                printf("%lld%c",ma[i][j]," \n"[j==m]);
    }
    void clear(){mem(ma,);}
};
int a ,b,c,d ,p,n;
pii f(int x,int y){
    if(!x)return make_pair(y,n);
    int l = max(y,(p+x+)/(x+)),r = min(n,p/x);
    return make_pair(l,r);
}

void solve(){
    scanf("%d%d%d%d%d%d",&a,&b,&c,&d,&p,&n);
    if(n==)printf("%d\n",a);
    if(n==)printf("%d\n",b);
    else{
        Matrix x(,),y(,);
        x[][] = b,x[][]=a,x[][]=;
        for(int i=;i<=n;){
            pii seg = f(p/i,i);
            y[][]=d,y[][] = ,y[][] = ;
            y[][]=c,y[][] = ,y[][] = ;
            y[][]=p/i,y[][]=,y[][] = ;
            x = x*(y^(seg.Y - seg.X  + ));
            i = seg.Y+;
        }
        printf("%lld\n",x[][] );
    }

    return;
}

int main()
{
//    freopen("F:\\in.txt","r",stdin);
//    freopen("out.txt","w",stdout);
//    ios::sync_with_stdio(false);
    int t = ;
    scanf("%d",&t);
    while(t--){
    //    printf("Case %d: ",cas++);
        solve();
    }
    return ;
}