PLSA的EM推导

本文作为em算法在图模型中的一个应用，推导plsa的em算法。

1 em算法

em算法是解决一类带有隐变量模型的参数估计问题。

1.1 模型的定义

输入样本为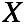，对应的隐变量为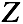。待估计的模型参数为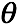，目标为极大化似然函数

对于上式的优化，不能通过直接对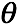进行求导，因为一旦求导，就有如下的形式：

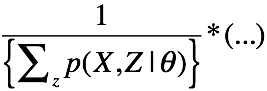
显然是不好求的。 

1.2 em算法的迭代过程

a. 初始化：随机初始参数的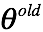 

b. E step：

            计算隐变量的后验分布

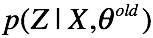
 c. M step:

          迭代参数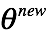

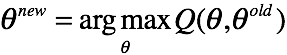
        其中，Q函数为X,Z的对数联合分布在Z的后验分布下的期望 

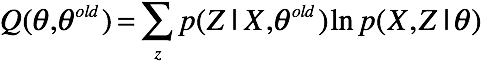上面的式子，将样本和隐变量都表示成矩阵的形式，让人有些不太好套公式。

2 高斯混合模型

2.1 基本模型

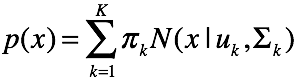 混合高斯模型认为，变量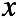服从一个多峰的高斯分布，由数个高斯分布组合而成。所以我们首先引入隐变量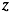，并且我们认为变量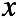通过这样一个过程生成。引入隐变量的高斯混合模型用图模型表示：

 

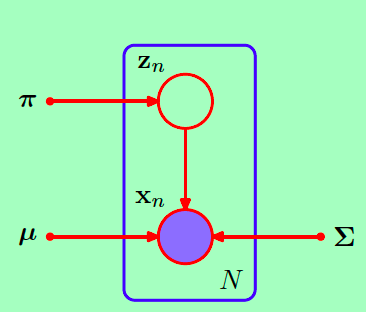
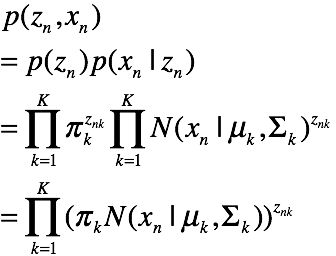
因此该图模型表示的联合概率为：

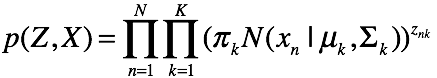2.2 em算法的推导

e step: 计算每一个样本的后验概率，遍历k等于1的各种情况

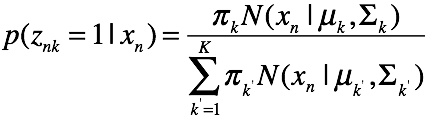
 M step: 首先推导Q方程

 

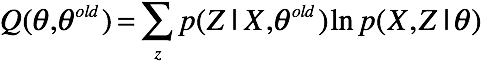
对于每一对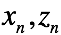

 

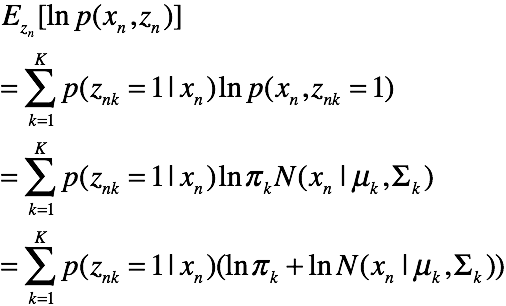
由于N个样本独立，所以有

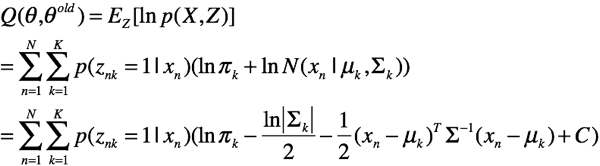
 好了，我们开始极大化这个期望

 

求均值

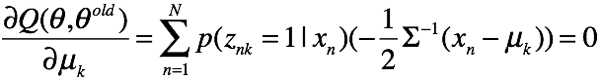 解方程得

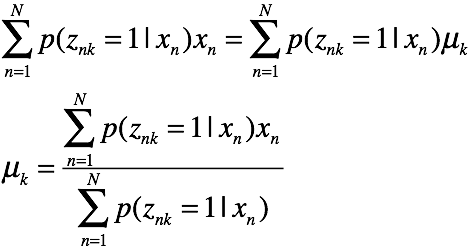
求方差比较复杂，直接给出结论：

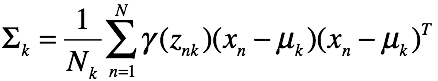
其中：

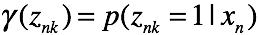
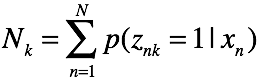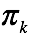 最后求,注意这里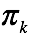的概率和为1，用拉格朗日乘子法解受限优化问题。有拉格朗日函数

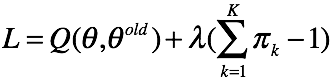
对 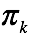求偏导有

 

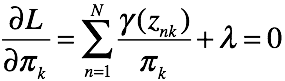
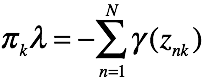
有k个关于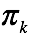的方程，对这些方程做累加有

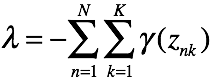
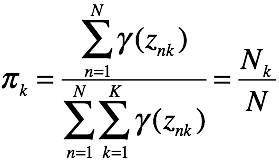 其中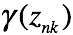，是概率，对k的累加和为1

至此，混合高斯模型的em迭代方法推导完毕，总结如下

E step:

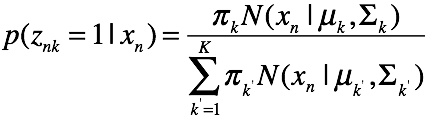
M step:

 

 

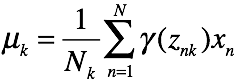
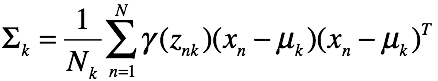
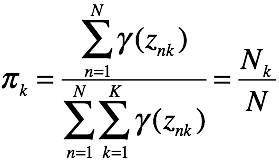
其中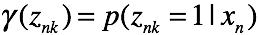

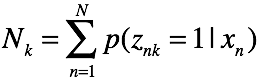
好了，我们完成了混合高斯模型的推导。混合高斯模型是一般高斯模型的推广，使得概率密度估计的外延得到扩展。另外，我们搞清楚了em算法使用的细节，在e step，我们求每一对(zn,xn)的后验概率和联合概率，遍历zn的所有情况，然后求每一个对数似然函数的期望，并在N上求和，就得到了目标函数。

 

3 PLSA主题模型

PLSA主题模型是比较老的模型了，逐渐被LDA这种更bayesian的方法取代了。我们来看看图模型。

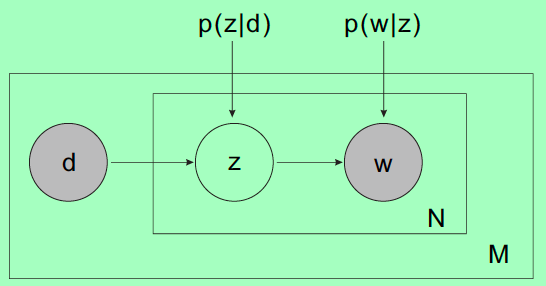
3.1 模型假设

对于一篇文档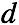,在每一个词的位置，首先选择一个topic，然后在topic的词分布中选择一个词作为当前位置的词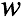。输入样本为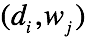，需要估计的参数为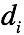在主题上的分布 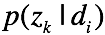,以及主题下词的分布。

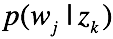首先求联合概率。对于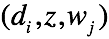这一Complete样本，

有联合概率

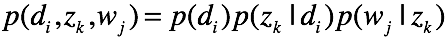
有后验概率

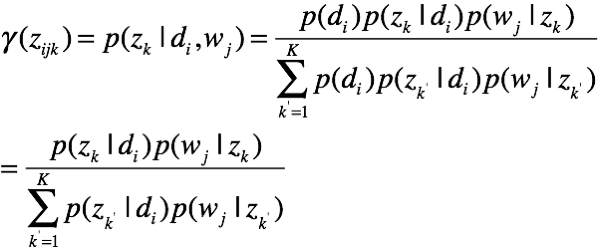有一对样本的期望函数

 

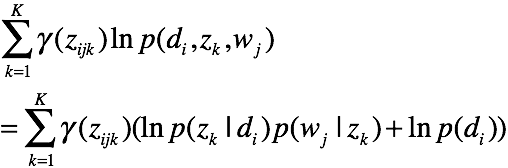
这里，我们取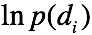为常数。得到了整体的期望函数

 这里，我们没有考虑词与词之间的相互顺序。接下来，我们要优化这个问题。

(1) 对于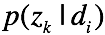，根据拉格朗日乘子法有代价函数：

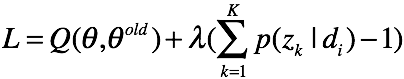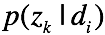对 求偏导，有

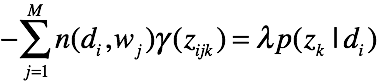
对K个主题方程求和，可得

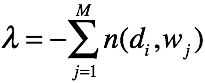
 可得

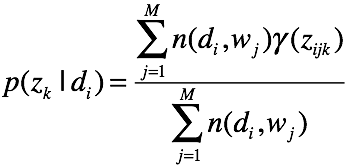
 (2) 对于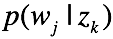，根据拉格朗日乘子法有代价函数：

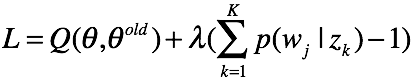
对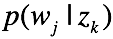求偏导，有

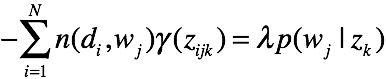
对M个词累加，可得

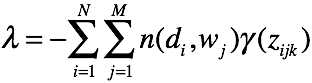
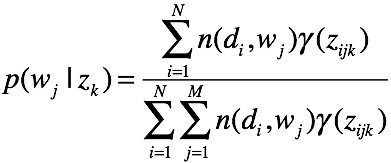 好的，我们可以总结一下过程了。

E step

计算后验概率

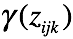
M step

迭代更新

 

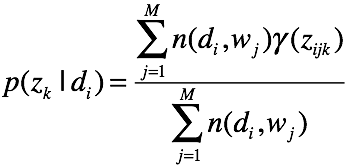
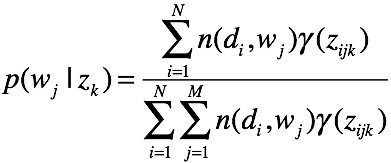
好了，我们推导了一遍混合高斯模型，又自行推导了一遍plsa.EM算法的精华基本掌握了。