KMP——强大的next数组

$KMP$ 的原理不在这里仔细讲了，主要说说最近刷题总结出的 $next$ 数组的强大功能。

部分例题来自《信息学奥赛一本通》的配套练习。

基于定义——字符串相同前后缀

“基于定义”：我们求的 $next$ 数组就是字符串到某一位时最长相同前后缀的长度。

注意 $next$ 数组求的为“最长”的，那如果想知道一个字符串所有相同的前后缀长度咋办？

举个栗子：

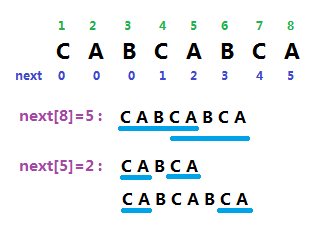
假设一个 $n$ 位的字符串（下标从 $1$ 到 $n$），$next[n]=p$

那么该字符串的子串 $[1,p]$ 与 $[n-p+1,n]$ 应是相同的

设 $next[p]=q$ ，那么子串 $[1,q]$ 与 $[p-q+1,p]$ 是相同的

综上，子串 $[1,q]$ 与 $[n-q+1,n]$ 是相同的，即 $next[next[n]]$ 也是该字符串相同前后缀长度

就这样 $next$ 一遍遍向前找，直到某一位的 $next$ 为 $0$，拓展出一棵 $next$ 树（也叫 $fail$ 树）。

例题 $bzoj3620$

$PROBLEM:$

求一个长度为 $n$ 的字符串所有形似 $A+B+A$ , 且 $len(A) \geq k,len(B) \geq 1$ 的子串数目。

$n \leq 15000$

$SOLUTION:$

一个奇妙的事情是这个题 $O(n^2)$ 能过。

于是枚举每一位为起点，$KMP$ 的过程中，$next$ 值相当于这一段子串 $len(A)$ 的最大值

如果它小于 $k$ ，显然不行。

而若 $它 \times 2+1 > 子串长度$ 也不行。

所以需要找到合适的 $len(A)$ 满足 $len(A) \geq k$ 且 $len(A) \times 2 +1 \leq 子串长度$

这就用到 $next$ 树的思想了！

还有一个小优化，用一个数组记录某一段 $\geq k$ 的最短的相同前后缀长度，把它作为 $len(A)$ 判断比较快。

代码：

#include<cstdio>

#include<iostream>

#include<algorithm>

#include<cstring>

using namespace std;

const int N = 15005;

char s[N];

int nxt[N],KK,ok[N],ans;

void KMP(char p[]){

    int len=strlen(p+1),k=0;

    nxt[1]=0; ok[0]=ok[1]=-1;

    for(int i=2;i<=len;i++){

        while(k && p[i]!=p[k+1]) k=nxt[k];

        if(p[i]==p[k+1]) k++;

        nxt[i]=k;

        if(k<KK) { ok[i]=-1; continue; }

        if(ok[k]==-1) ok[i]=k;

        else ok[i]=ok[k];

        if(ok[i]*2+1<=i) ans++;

    }

}

int main()

{

    int len;

    scanf("%s",s+1);

    scanf("%d",&KK);

    len=strlen(s+1);

    for(int i=1;i<=len;i++) {

        if(KK*2+1>len-i+1) break;

        KMP(s+i-1);

    }

    printf("%d\n",ans);

    return 0;

}

拓展功能——字符串循环节

“拓展”：这里的主角为 $n-next[n]$

还是举个栗子：

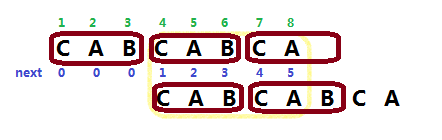
上图中 $n-next[n]=3$ ，那 $3$ 是什么呢？

看那些棕圈圈，$3$ 其实可以叫做字符串的 “类”循环节，因为字符串并不是由这个循环节完完整整组成的。

而若一个字符串有真正的循环节要满足什么条件呢？

答案是 $n-next[n]$ 整除 $n$

同样举个栗子就明了了：

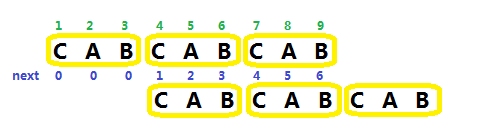
对于所有字符串， $n-next[n]$ 只是它最短的循环节（类循环节），其他循环节（类循环节）的长度通过 $next$ 一遍遍向前找求出。

还是 $next$ 树的思想，结合栗子即可证明，这里就不赘述了。

！！！

注意：有真正循环节的字符串，所有循环节长度都为最短循环节长度的倍数。而类循环节并不满足这一性质！

例题1 $bzoj1511$

$PROBLEM:$

一个串是有限个小写字符的序列,特别的,一个空序列也可以是一个串. 一个串 $P$ 是串 $A$ 的前缀, 当且仅当存在串 $B$ , 使得 $A = PB$. 如果 $P \neq A$ 并且 $P$ 不是一个空串,那么我们说 $P$ 是 $A$ 的一个 $proper$ 前缀. 定义 $Q$ 是 $A$ 的周期, 当且仅当 $Q$ 是 $A$ 的一个 $proper$ 前缀并且 $A$ 是 $QQ$ 的前缀(不一定要是 $proper$ 前缀). 比如串 $abab$ 和 $ababab$ 都是串 $abababa$ 的周期. 串 $A$ 的最大周期就是它最长的一个周期或者是一个空串(当 $A$ 没有周期的时候), 比如说, $ababab$ 的最大周期是 $abab$. 串 $abc$ 的最大周期是空串. 给出一个串,求出它所有前缀的最大周期长度之和.

$串长度 \leq 10^6$

$SOLUTION:$

其实题中说的最大周期就是 $\neq A$ 的最长“类循环节”

$next$ 树的思想，用一个数组记录每个“点”在该“树”上最小的非零祖先，否则会超时

#include<cstdio>

#include<iostream>

#include<algorithm>

using namespace std;

const int N = 1000005;

typedef long long ll;

int n;

int nxt[N],snxt[N];

char s[N];

int main()

{

	scanf("%d",&n);

	scanf("%s",s+1);

	ll ans=0;

	int k=0;

	nxt[1]=0; snxt[1]=1;

	for(int i=2;i<=n;i++){

		while(k && s[i]!=s[k+1]) k=nxt[k];

		if(s[i]==s[k+1]) k++;

		nxt[i]=k;

		snxt[i]=(k?snxt[k]:i);

		ans+=i-snxt[i];

	}

	printf("%lld\n",ans);

	return 0;

}

例题2 $bzoj4974$

$PROBLEM:$

一个串 $T$ 是 $S$ 的循环节，当且仅当存在正整数 $k$，使得 $S$ 是 $T^k$ (即 $T$ 重复 $k$ 次)的前缀，比如 $abcd$ 是 $abcdabcdab$ 的循环节。给定一个长度为 $n$ 的仅由小写字符构成的字符串 $S$，请对于每个 $k(1 \leq k \leq n)$，求出 $S$ 长度为 $k$ 的前缀的最短循环节的长度 $per_i$ 。小 $Q$ 告诉你 $n$ 以及 $per_1,per_2,...,per_n$，请找到一个长度为 $n$ 的小写字符串 $S$，使得 $S$ 能对应上 $per$ 。

$n \leq 10^5$

$SOLUTION:$

可以发现，$per_i$ 值其实就是最短“类循环节”长度，也就是 $n-next[i]$

于是我们可以求出所有 $next$ 值，然后进行逆向 $KMP$ ，得出原字符串。

代码：

#include<cstdio>

#include<iostream>

#include<algorithm>

using namespace std;

const int N = 100005;

int n;

int nxt[N],vis[26];

char s[N];

int main()

{

    scanf("%d",&n);

    for(int i=1;i<=n;i++) scanf("%d",&nxt[i]),nxt[i]=i-nxt[i];

    s[1]='a';

    for(int i=2;i<=n;i++){

        if(nxt[i]!=0) { s[i]=s[nxt[i]]; continue; }

        for(int j=0;j<26;j++) vis[j]=0;

        int k=nxt[i-1];

        while(k!=0) vis[s[k+1]-'a']=1,k=nxt[k];

        vis[s[k+1]-'a']=1;

        for(int j=0;j<26;j++)

            if(!vis[j]) { s[i]='a'+j; break; }

    }

    printf("%s",s+1);

    return 0;

}