JAVA算法之高级排序

　　本章介绍两种高级排序，希尔排序和快速排序，这两种排序比之前讲到的简单排序都要快很多；希尔排序大约需要O(N*(logN)²)的时间，快速排序的时间复杂度为(N*logN)，这两种算法和我们在讲递归的时候讲到的归并排序不同，不需要大量的辅助存储空间，快速排序是所有通用排序算法中最快的排序算法。

希尔排序：

　　希尔排序是基于插入排序的，希尔排序在插入排序的基础之上通过加大插入排序元素之间的间隔，并在这些间隔元素之间进行插入排序，使数据实现大跨度的移动，从而使排序更有效率，我们习惯将排序时数据项之间的间隔称为增量，用h来表示，下图表示了十个数据项，以增量为4进行第一趟排序后的结果

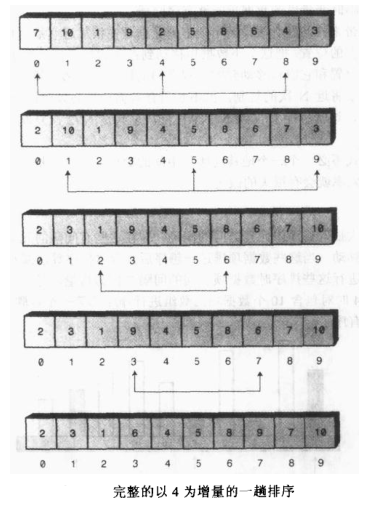
　　通过上面的一趟排序之后我们可以看到元素离他们的最终有序序列位置都很近了，希尔排序就是通过创建这种交错有序的数据项集合，从而提高排序的效率，当上面完成了4增量的排序之后，就可以进行普通的插入排序，这样就比普通的插入排序的效率要高很多。

　　上面对于有十个数据项的数组初始增量我们设置为4，对于数据项更大的数组我们的初始增量也应该设置得更大，这里我们使用Knuth提出的间隔序列，序列的通项表达式为h=3*h+1，假设我们数据项的个数为100，那么通过Knuth间隔序列1,4,13,40,121,364,1093这里1093大于了我们的数据项1000，所以我们取初始的增量为364然后通过Knuth间隔序列依次减小我们的增量值，最终达到我们想要的一个个排序的效果，接下来我们给出希尔排序的java代码

public class ArrayShell {

    public long[] theArray;
    private int nElems;

    public ArrayShell(int size) {
        this.theArray = new long[size];
        this.nElems = 0;
    }

    public void insert(long value) {
        theArray[nElems++] = value;
    }

    public void shellSort() {
        //首先找到初始增量
        int h = 1;
        int outer, inner;
        while (h <= nElems/3) {
            h = 3 * h + 1;
        }
        while (h > 0) {
            //以下就是普通的插入排序，只是步长换为h即可
            for (outer = h; outer < nElems; outer++) {
                long temp = theArray[outer];
                //增量为h，所以我们首个比较的元素从h开始，h和第一个索引为0的元素比较大小、h+1和索引为1比较是否交换。然后以此类推
                inner = outer;
                while (inner > h - 1 && temp < theArray[inner - h]) {  //需要进行数据交换的元素的满足条件
                    theArray[inner] = theArray[inner - h];
                    inner -= h;
                }
                theArray[inner] = temp;
            }
            //从最大增量一直递减到1做插入排序
            h = (h - 1) / 3;
        }
    }
}

希尔排序中间隔序列互质很重要，他能是每一趟排序更有可能保持前一趟已排序好的效果。

快速排序

　　快速排序是基于划分算法之上的一种排序算法，首先我们介绍一下划分算法的基本原理

• 划分

　　划分的基本原理就是把数据分为两组，使关键值大于特定值的数据在一组，使关键值小于特定值的数据在另一组，比如我们日常生活中将家距离办公点15km以内和以外的雇员分为两组。划分算法中我们将两个标记分别指向数组的两头，左边的标记leftPtr ，向右移动，右边的标记 rightPtr，向左移动，当leftPtr遇到比枢纽小的数据项时，继续向右移动，当遇到比枢纽大的数据项时就停下来，同样当rightPtr遇到比枢纽大的数值的时候继续向左移动，遇到比枢纽小的就停下来，然后需要交换这两个数据项。交换之后继续移动指针，重复上面的步骤，知道两个标记的值相等的时候则划分算法完成。

　　接下来我们看划分算法的java代码

class ArrayPar {
    public Long[] theArray;
    private int nElems;
    public ArrayPar(int max) {
        theArray = new Long[max];
        this.nElems = 0;
    }
    public void insert(Long value) {
        theArray[nElems] = value;
        nElems++;
    }
    public int partitionIt(int leftPtr, int rightPtr, long pivot) {
        while (true) {
            //当leftPtr遇到比枢纽小的数据项时，继续向右移动(即 leftPtr++)，当遇到比枢纽大的数据项时就停下来
            while (leftPtr < rightPtr && theArray[leftPtr] <= pivot)    //防止索引越界加上leftPtr<rightPtr的判断
                leftPtr++;
            //当rightPtr遇到比枢纽大的数据项时，继续向左移动(即 rightPtr--)，当遇到比枢纽大的数据项时就停下来
            while (rightPtr > leftPtr && theArray[rightPtr] >= pivot)
                rightPtr--;
            //当leftPtr标记大于等于right标记的时候结束外层循环，否则交换两个标记的数据项
            if (leftPtr >= rightPtr)
                break;
            else
                swap(leftPtr, rightPtr);
        }
        return leftPtr;
    }
    /**交换数据方法*/
    public void swap(int dex1, int dex2) {
        long temp = theArray[dex1];
        theArray[dex1] = theArray[dex2];
        theArray[dex2] = temp;
    }
}

• 快速排序

　　快速排序的执行时间为O（N*logN）级，快速排序是基于划分算法之上的，利用递归的思想的一种排序算法，这里我们选择数组的最右边的元素作为枢纽，在划分算法完成之后，需要在之前的算法的基础上加一步，将枢纽项和右数组的起始项进行位置交换，交换后的枢纽值的顺序就是最终的顺序，然后在利用递归将划分后的左右数组进行上述步骤。首先我们来看看快速排序的java代码

class ArrayPar {
    public Long[] theArray;
    private int nElems;

    public ArrayPar(int max) {
        theArray = new Long[max];
        this.nElems = 0;
    }

    public void insert(Long value) {
        theArray[nElems] = value;
        nElems++;
    }

    public int partitionIt(int leftPtr, int rightPtr, long pivot) {
        int right = rightPtr;
        while (true) {
            //当leftPtr遇到比枢纽小的数据项时，继续向右移动(即 leftPtr++)，当遇到比枢纽大的数据项时就停下来
            while (leftPtr < rightPtr && theArray[leftPtr] <= pivot)    //防止索引越界加上leftPtr<rightPtr的判断
                leftPtr++;
            //当rightPtr遇到比枢纽大的数据项时，继续向左移动(即 rightPtr--)，当遇到比枢纽大的数据项时就停下来
            while (rightPtr > leftPtr && theArray[rightPtr] >= pivot)
                rightPtr--;
            //当leftPtr标记大于等于right标记的时候结束外层循环，否则交换两个标记的数据项
            if (leftPtr >= rightPtr)
                break;
            else
                swap(leftPtr, rightPtr);
        }
        swap(leftPtr,right);    //最后将当前枢纽数值放入对应的排序位置
        return leftPtr;
    }

    /**
     * 交换数据方法
     */
    public void swap(int dex1, int dex2) {
        long temp = theArray[dex1];
        theArray[dex1] = theArray[dex2];
        theArray[dex2] = temp;
    }
    /***快速排序的方法*/
    public void recQuickSort(int left, int right) {
        if (right - left <= 0)  //这里是递归的基值条件，当只有一个数据项的时候结束递归
            return;
        else {
            long pivot = theArray[right];     //选择最右边的数据作为划分的枢纽数据
            int partition = partitionIt(left, right, pivot);    //调用划分的算法
            //然后将划分好的两部分利用递归的思想进行再次划分排序
            recQuickSort(left, partition - 1);
            recQuickSort(partition + 1, right);
        }
    }
}

下图显示了快速排序的过程

上面就是希尔排序算法和快速排序算法的所有内容