机器学习——决策树,DecisionTreeClassifier参数详解,决策树可视化查看树结构
0.决策树
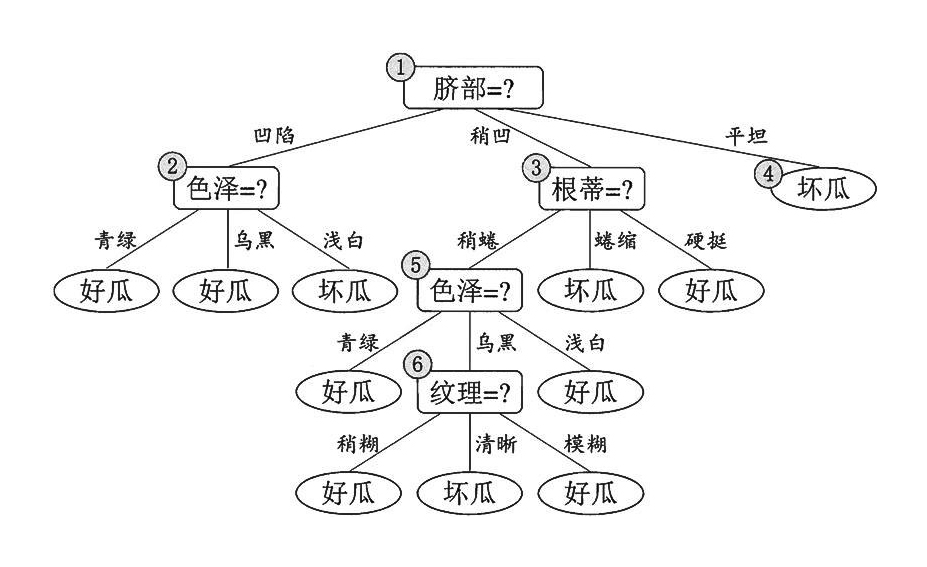
决策树是一种树型结构,其中每个内部节结点表示在一个属性上的测试,每一个分支代表一个测试输出,每个叶结点代表一种类别。
决策树学习是以实例为基础的归纳学习
决策树学习采用的是自顶向下的递归方法,其基本思想是以信息熵为度量构造一棵熵值下降最快的树。到叶子节点的处的熵值为零,此时每个叶结点中的实例都属于同一类。
1.决策树学习算法的特点
决策树算法的最大优点是可以自学习。在学习的过程中,不需要使用者了解过多知识背景,只需要对训练实例进行较好的标注,就能够进行学习了。
在决策树的算法中,建立决策树的关键,即在当前状态下选择哪个属性作为分类依据。根据不同的目标函数,建立决策树主要有一下三种算法:
- ID3
- C4.5
- CART
主要的区别就是选择的目标函数不同,ID3使用的是信息增益,C4.5使用信息增益率,CART使用的是Gini系数。
2.信息熵
在信息论与概率统计中,熵(entropy)是表示随机变量不确定性的度量。设X是一个区有限个值的离散随机变量,其概率分布为:

则随机变量X的熵的定义为:
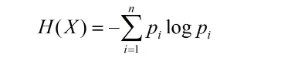
在上述式中,若pi=0,则定义0log0=0,通常,式中的对数以2为底或者以e为底(自然对数),这时熵的单位分别称作比特(bit)或者纳特(nat)。由定义可知,熵只依赖于X的分布,而与X的取值无关,所以也可以将X的熵记作H(p),即:

熵越大,随机变量的不确定性就越大。从定义可以验证
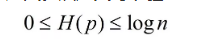
当随机变量确定时,熵的值最小为0,当熵值最大时,随机变量不确定性最大。
设有随机变量(X,Y),其联合概率分布为
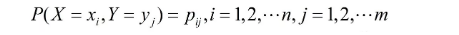
条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性,随机变量X给定的条件下随机变量Y的条件熵H(Y|X),定义为X给定条件下Y的条件概率分布的熵对X的数学期望:
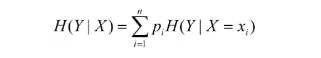
这里,pi=P(X=xi),i=1,2,......,n
当熵和条件熵中的概率是有数据估计(极大似然估计)得到时,所对应的熵与条件熵分别称为经验熵和条件经验熵。此时,如果有0概率,则令0log0=0.
信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。
特征A对数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A的经验条件熵H(D|A)之差,即:
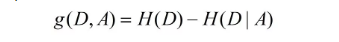
一般地,熵H(Y)与条件熵H(Y|X)之差称为互信息。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。
3.模型建立
具体的决策树算法流程,我们在这里就不仔细介绍了,详细算法可以参阅李航老师的《统计学习方法》一书。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.tree import DecisionTreeClassifier def iris_type(s):
it = {b'Iris-setosa': 0, b'Iris-versicolor': 1, b'Iris-virginica': 2}
return it[s] iris_feature = u'花萼长度', u'花萼宽度', u'花瓣长度', u'花瓣宽度' if __name__ == "__main__":
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False path = '../dataSet/iris.data' # 数据文件路径
data = np.loadtxt(path, dtype=float, delimiter=',', converters={4: iris_type})
x_prime, y = np.split(data, (4,), axis=1) feature_pairs = [[0, 1], [0, 2], [0, 3], [1, 2], [1, 3], [2, 3]]
plt.figure(figsize=(10, 9), facecolor='#FFFFFF')
for i, pair in enumerate(feature_pairs):
# 准备数据
x = x_prime[:, pair] # 决策树学习
clf = DecisionTreeClassifier(criterion='entropy', min_samples_leaf=3)
dt_clf = clf.fit(x, y) # 画图
N, M = 500, 500
x1_min, x1_max = x[:, 0].min(), x[:, 0].max()
x2_min, x2_max = x[:, 1].min(), x[:, 1].max()
t1 = np.linspace(x1_min, x1_max, N)
t2 = np.linspace(x2_min, x2_max, M)
x1, x2 = np.meshgrid(t1, t2)
x_test = np.stack((x1.flat, x2.flat), axis=1) y_hat = dt_clf.predict(x)
y = y.reshape(-1)
c = np.count_nonzero(y_hat == y) # 统计预测正确的个数
print('特征: ', iris_feature[pair[0]], ' + ', iris_feature[pair[1]])
print('\t预测正确数目:', c)
print('\t准确率: %.2f%%' % (100 * float(c) / float(len(y)))) # 显示
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
y_hat = dt_clf.predict(x_test) # 预测值
y_hat = y_hat.reshape(x1.shape)
plt.subplot(2, 3, i+1)
plt.pcolormesh(x1, x2, y_hat, cmap=cm_light)
plt.scatter(x[:, 0], x[:, 1], c=y, edgecolors='k', cmap=cm_dark)
plt.xlabel(iris_feature[pair[0]], fontsize=14)
plt.ylabel(iris_feature[pair[1]], fontsize=14)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.grid()
plt.suptitle(u'决策树对鸢尾花数据的两特征组合的分类结果', fontsize=18)
plt.tight_layout(2)
plt.subplots_adjust(top=0.92)
plt.show()
在书面的代码中,为了可视化的方便,我们采用特征组合的方式,将鸢尾花的四个两两进行组合,分别建立决策树模型,并对其进行验证。
DecisionTreeClassifier(criterion='entropy', min_samples_leaf=3)函数为创建一个决策树模型,其函数的参数含义如下所示:
- criterion:gini或者entropy,前者是基尼系数,后者是信息熵。
- splitter: best or random 前者是在所有特征中找最好的切分点 后者是在部分特征中,默认的”best”适合样本量不大的时候,而如果样本数据量非常大,此时决策树构建推荐”random” 。
- max_features:None(所有),log2,sqrt,N 特征小于50的时候一般使用所有的
- max_depth: int or None, optional (default=None) 设置决策随机森林中的决策树的最大深度,深度越大,越容易过拟合,推荐树的深度为:5-20之间。
- min_samples_split:设置结点的最小样本数量,当样本数量可能小于此值时,结点将不会在划分。
- min_samples_leaf: 这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝。
- min_weight_fraction_leaf: 这个值限制了叶子节点所有样本权重和的最小值,如果小于这个值,则会和兄弟节点一起被剪枝默认是0,就是不考虑权重问题。
- max_leaf_nodes: 通过限制最大叶子节点数,可以防止过拟合,默认是"None”,即不限制最大的叶子节点数。
- class_weight: 指定样本各类别的的权重,主要是为了防止训练集某些类别的样本过多导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重,如果使用“balanced”,则算法会自己计算权重,样本量少的类别所对应的样本权重会高。
- min_impurity_split: 这个值限制了决策树的增长,如果某节点的不纯度(基尼系数,信息增益,均方差,绝对差)小于这个阈值则该节点不再生成子节点。即为叶子节点 。
plt.suptitle(u'决策树对鸢尾花数据的两特征组合的分类结果', fontsize=18)设置整个大画布的标题
plt.tight_layout(2) 调整图片的布局
plt.subplots_adjust(top=0.92) 自适应,绘图距顶部的距离为0.92
结果如下:
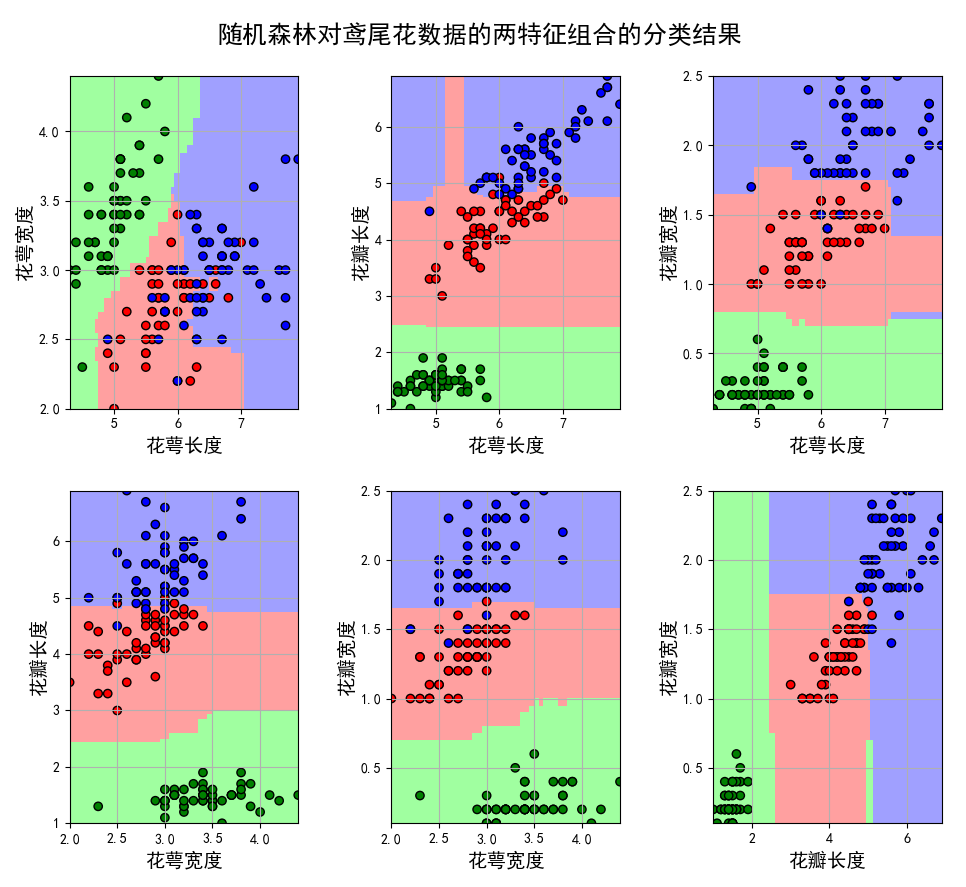
不同的特征组合的决策树模型的准确率:

4.决策树的保存
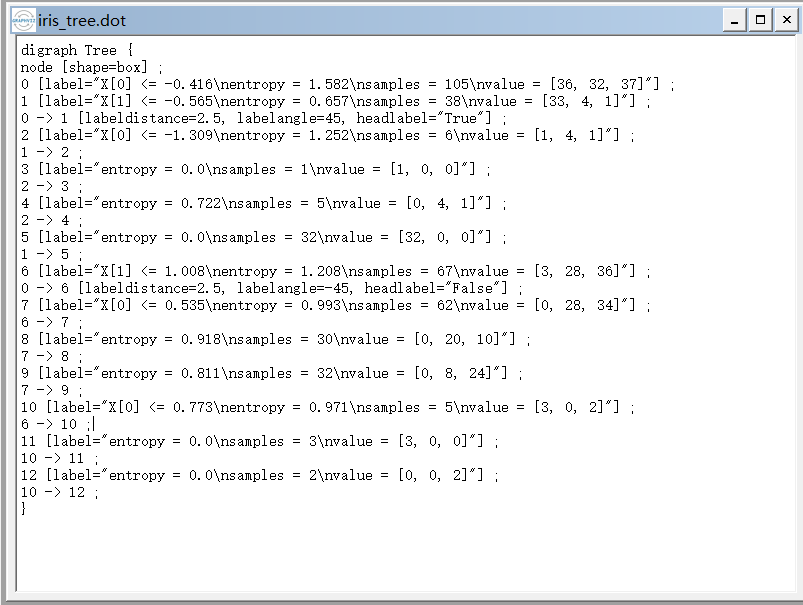
当我们通过建立好决策树之后,我们应该怎样查看建立好的决策树呢?sklearn已经帮助我们写好了方法,代码如下:
from sklearn import tree #需要导入的包
f = open('../dataSet/iris_tree.dot', 'w')
tree.export_graphviz(model.get_params('DTC')['DTC'], out_file=f)
当我们运行之后,程序会生成一个.dot的文件,我们能够通过word打开这个文件,你看到的是树节点的一些信息,我们通过graphviz工具能够查看树的结构:
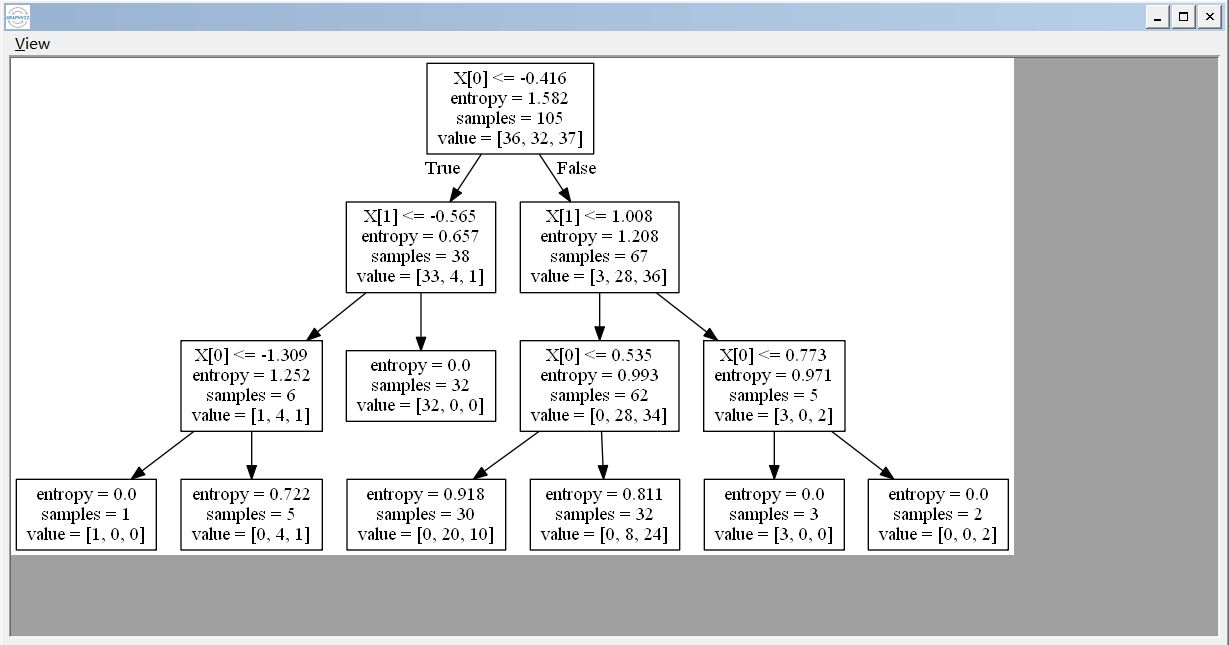
机器学习——决策树,DecisionTreeClassifier参数详解,决策树可视化查看树结构的更多相关文章
- crontab 各参数详解及如何查看日志记录
详见:http://blog.yemou.net/article/query/info/tytfjhfascvhzxcyt145 crontab各参数说明: crontab [-u user] [fi ...
- 机器学习——KMeans聚类,KMeans原理,参数详解
0.聚类 聚类就是对大量的未知标注的数据集,按数据的内在相似性将数据集划分为多个类别,使类别内的数据相似度较大而类别间的数据相似度较小,聚类属于无监督的学习方法. 1.内在相似性的度量 聚类是根据数据 ...
- 以太坊客户端Geth命令用法-参数详解
Geth在以太坊智能合约开发中最常用的工具(必备开发工具),一个多用途的命令行工具. 熟悉Geth可以让我们有更好的效率,大家可收藏起来作为Geth命令用法手册. 本文主要是对geth help的翻译 ...
- 【机器学习基本理论】详解最大似然估计(MLE)、最大后验概率估计(MAP),以及贝叶斯公式的理解
[机器学习基本理论]详解最大似然估计(MLE).最大后验概率估计(MAP),以及贝叶斯公式的理解 https://mp.csdn.net/postedit/81664644 最大似然估计(Maximu ...
- 【机器学习基本理论】详解最大后验概率估计(MAP)的理解
[机器学习基本理论]详解最大后验概率估计(MAP)的理解 https://blog.csdn.net/weixin_42137700/article/details/81628065 最大似然估计(M ...
- Echarts dataZoom缩放功能参数详解:
dataZoom=[ //区域缩放 { id: 'dataZoomX', show:true, //是否显示 组件.如果设置为 false,不会显示,但是数据过滤的功能还存在. backgroundC ...
- VLC命令行参数详解
VLC命令行参数详解 2012-11-29 14:00 6859人阅读 评论(0) 收藏 举报 Usage: vlc [options] [stream] ...You can specify mul ...
- Nginx主配置参数详解,Nginx配置网站
1.Niginx主配置文件参数详解 a.上面博客说了在Linux中安装nginx.博文地址为:http://www.cnblogs.com/hanyinglong/p/5102141.html b.当 ...
- iptables参数详解
iptables参数详解 搬运工:尹正杰 注:此片文章来源于linux社区. Iptalbes 是用来设置.维护和检查Linux内核的IP包过滤规则的. 可以定义不同的表,每个表都包含几个内部的链,也 ...
随机推荐
- 让Tomcat告别频繁重启
在网站开发过程中,有一个很烦的问题就是每次我们在项目里增加几行代码,然后我们企图在浏览器中查看修改后的变化时,却发现浏览器的内容并不变化,于是我们只能通过频繁的重启tomcat来获得最新的效果,其实这 ...
- 关于Random(47)与randon.nextInt(100)的区别
参考https://blog.csdn.net/md_shmily92/article/details/44059313 相关文章random.nextInt()与Math.random()基础用法 ...
- MySQL 开发实践 8 问,你能 hold 住几个?
最近研发的项目对DB依赖比较重,梳理了这段时间使用MySQL遇到的8个比较具有代表性的问题,答案也比较偏自己的开发实践,没有DBA专业和深入,有出入的请使劲拍砖!- MySQL读写性能是多少,有哪些性 ...
- Java 链接SQL Server 数据库
1 //Java 连接 SQL Server数据库 2 public static final String DRIVERNAME="com.microsoft.sqlserver.jdbc ...
- hdu 2899 Strange fuction 模拟退火
求 F(x) = 6 * x^7+8*x^6+7*x^3+5*x^2-y*x (0 <= x <=100)的最小值 模拟退火,每次根据温度随机下个状态,再根据温度转移 #include& ...
- jdbc 增删改查以及遇见的 数据库报错Can't get hostname for your address如何解决
最近开始复习以前学过的JDBC今天肝了一晚上 来睡睡回笼觉,长话短说 我们现在开始. 我们先写一个获取数据库连接的jdbc封装类 以后可以用 如果不是maven环境的话在src文件下新建一个db.pr ...
- java的Integer与int的比较
- Vue-CLI和脚手架
但我们学习Vue时,很多教程都会说到用Vue-CLI构建项目,那么什么是脚手架?什么是Vue-CLI?为什么要用脚手架,好处在哪?以及为何我们用Vue开发项目时要用到Vue-CLI? 首先,CLI为c ...
- eclipse使用Git基本流程
1.安装GIT 2.Git的使用 ①下载代码到eclipse(右键导入工程) ②提交代码到本地(commit) ③更新代码到本地(pull) ④当本地出现冲突时,解决冲突,没有冲突当然就最好啦 ⑤提交 ...
- 【.NETCore开源】开弓没有回头箭
2019.2.11 开工大吉!经过了半个月的休假,今天回归岗位重新拾起工作,却发现熟悉的代码生疏了.年前的计划回忆不起来了,俗称"节后综合症". 忆半月圈子 过年放假的前几天有多篇 ...
