CF集萃2

CF1155D - Beautiful Array

题意：给你一个序列和x，你可以选择任意一个子串(可以为空)乘上x，使得得到的序列最大子串和最大。求这个最大值。30w，2s。

解：设f_i,0/1/2表示序列前i个数还没乘x/正在乘x/乘完了x的最大后缀和。答案就是这个DP数组的最大值。

 #include <bits/stdc++.h>

 typedef long long LL;
 const int N = ;

 LL a[N], x, f[N][];
 int n;

 int main() {
     scanf("%d%lld", &n, &x);
     for(int i = ; i <= n; i++) {
         scanf("%lld", &a[i]);
     }
     LL ans = ;
     for(int i = ; i <= n; i++) {
         f[i][] = std::max(a[i], f[i - ][] + a[i]);
         f[i][] = std::max(std::max(a[i] * x, f[i - ][] + a[i] * x), f[i - ][] + a[i] * x);
         f[i][] = std::max(a[i], std::max(f[i - ][] + a[i], f[i - ][] + a[i]));
         ans = std::max(std::max(ans, f[i][]), std::max(f[i][], f[i][]));
     }
     printf("%lld\n", ans);
     return ;
 }

AC代码

本题还有一种线段树做法。从左往右扫一遍，在每个位置考虑乘x的那一段的右端点在当前位置时的最大值。

那么右边要加上一个最大前缀。左边要在线段树上每个位置，维护以当前位置为乘x左端时的最大值。就是最大后缀 + (x - 1)a[i]

然后求个最大值就行了。

CF1117C - Magic Ship

题意：你要从(x1,y1)到(x2,y2)，你每天会走一格，还会被风吹一格。风向有个长为n的循环节。求最少要几天到达。n <= 1e5，坐标<=1e9。

解：发现某一天到达之后，接下来所有天都有办法到达。于是二分。

 #include <bits/stdc++.h>

 typedef long long LL;
 const int N = ;

 int x1, x2, Y1, Y2, n;
 char str[N];
 int dx[N], dy[N];

 template <typename T> inline T abs(T x) {
     return x <  ? -x : x;
 }

 inline bool check(LL k) {
     LL x = x1 + (k / n) * dx[n] + dx[k % n];
     LL y = Y1 + (k / n) * dy[n] + dy[k % n];
     return abs(x - x2) + abs(y - Y2) <= k;
 }

 int main() {
     scanf("%d%d%d%d", &x1, &Y1, &x2, &Y2);

     scanf("%d", &n);
     scanf("%s", str + );

     for(int i = ; i <= n; i++) {
         dx[i] = dx[i - ];
         dy[i] = dy[i - ];
         if(str[i] == 'U') {
             dy[i]++;
         }
         if(str[i] == 'D') {
             dy[i]--;
         }
         if(str[i] == 'L') {
             dx[i]--;
         }
         if(str[i] == 'R') {
             dx[i]++;
         }
     }

     LL l = , r = 1e18;
     while(l < r) {
         LL mid = (l + r) >> ;
         if(check(mid)) {
             r = mid;
         }
         else {
             l = mid + ;
         }
     }

     if(r == 1e18) r = -;
     printf("%lld\n", r);
     return ;
 }

AC代码

CF1117D - Magic Gems

题意：你有很多个魔法宝石，每个可以变成m个普通宝石。你需要选出若干个魔法宝石，然后再选出若干个把它们变成普通宝石，以此来填满n个空格。问方案数。n <= 1e18，m <= 100。

解：枚举选多少个魔法宝石，发现答案其实就是这个东西：

打表后发现f_n = f_n-1 + f_n-m。然而我们还有一种更优秀的推法：考虑最后一个空位是普通宝石还是魔法宝石即可。矩阵快速幂即可。

 #include <bits/stdc++.h>

 typedef long long LL;
 const int N = , MO = 1e9 + ;

 int a[N][N], c[N][N], m, ans[N][N];
 LL n;

 inline void out(int (*a)[N]) {

     for(int i = ; i <= m; i++) {
         for(int j = ; j <= m; j++) {
             printf("%d ", a[i][j]);
         }
         puts("");
     }
     puts("");

     return;
 }

 inline void mul() {
     memset(c, , sizeof(c));
     for(int k = ; k <= m; k++) {
         for(int i = ; i <= m; i++) {
             if(!ans[i][k]) {
                 continue;
             }
             for(int j = ; j <= m; j++) {
                 c[i][j] = (c[i][j] + 1ll * ans[i][k] * a[k][j] % MO) % MO;
             }
         }
     }
     memcpy(ans, c, sizeof(ans));
     return;
 }

 inline void mulself() {
     memset(c, , sizeof(c));
     for(int k = ; k <= m; k++) {
         for(int i = ; i <= m; i++) {
             if(!a[i][k]) continue;
             for(int j = ; j <= m; j++) {
                 c[i][j] = (c[i][j] + 1ll * a[i][k] * a[k][j] % MO) % MO;
             }
         }
     }
     memcpy(a, c, sizeof(c));
     return;
 }

 int main() {
     scanf("%lld%d", &n, &m);

     if(n < m) {
         printf("");
         return ;
     }

     for(int i = ; i < m; i++) {
         a[i + ][i] = ;
     }
     a[][m] = a[m][m] = ;
     for(int i = ; i <= m; i++) ans[i][i] = ;

     LL t = n - m;
     //out(a);
     //out(ans);
     while(t) {
         if(t & ) {
             mul();
             //out(ans);
         }
         mulself();
         //out(a);
         t = t >> ;
     }

     int res = ;
     for(int i = ; i <= m; i++) {
         res = (res + ans[i][m]) % MO;
     }
     res = (res + ans[m][m]) % MO;

     printf("%d\n", res);
     return ;
 }

AC代码

CF1117E - Decypher the String

题意：存在一个长为n的字符串和n个swap操作，但是你都不知道。你只知道操作的结果。你可以询问三次，每次给定一个字符串，回答该字符串操作的结果。输出原串。n <= 10000。

解：可用的字符有26个。假如每次把集合s位置的字符变成a，那么操作后所有a的位置集合t和s之间就有一个双射。这样一次就可以把n / 26。发现26³ = 17576，刚好。

实现上就是用一个结构体表示一组双射，两个vector存s和t。每次把这个vector分段染色，然后输出，操作完之后进行分组。

 #include <bits/stdc++.h>

 const int N = ;
 /// 26 * 26 = 676
 struct Node {
     std::vector<int> a, b;
 }stk[N]; int top;

 char str[N], my[N];
 int n;

 inline void solve(const Node &x) {
     int lm;
     if(x.a.size() <= ) {
         lm = ;
     }
     else if(x.a.size() <= ) {
         lm = ;
     }
     else {
         lm = ;
     }
     int p = ;
     char c = 'a';
     for(int i = ; i < (int)x.a.size(); i++) {
         my[x.a[i]] = c;
         ++p;
         if(p == lm) {
             p = ;
             ++c;
         }
     }
     return;
 }

 inline void work(int i) {
     int lm;
     if(stk[i].a.size() <= ) {
         lm = ;
     }
     else if(stk[i].a.size() <= ) {
         lm = ;
     }
     else {
         lm = ;
     }
     int p = , cnt = , f;
     for(int j = ; j < (int)stk[i].a.size(); j++) {
         stk[top + cnt].a.push_back(stk[i].a[j]);
         ++p;
         f = cnt;
         if(p == lm) {
             p = ;
             ++cnt;
         }
     }

     for(int j = ; j < (int)stk[i].a.size(); j++) {
         int x = stk[i].b[j];
         stk[top +  - 'a' + my[x]].b.push_back(x);
     }
     stk[i] = stk[top + f];
     stk[top + f].a.clear(); /// !!! important
     stk[top + f].b.clear(); ///
     top = top + f - ;
     return;
 }

 int main() {
     scanf("%s", str + );
     n = strlen(str + );

     top = ;
     for(int i = ; i <= n; i++) {
         stk[].a.push_back(i);
         stk[].b.push_back(i);
         my[i] = 'a';
     }

     for(int t = ; t <= ; t++) {
         //printf("t = %d \n", t);
         for(int i = ; i <= top; i++) {
             //printf("i = %d \n", i);
             if(stk[i].a.size() > ) {
                 solve(stk[i]);
             }
         }
         printf("? ");
         for(int i = ; i <= n; i++) {
             putchar(my[i]);
         }
         puts("");
         fflush(stdout);
         scanf("%s", my + );
         int temp = top;
         for(int i = ; i <= temp; i++) {
             if(stk[i].a.size() > ) {
                 work(i);
             }
         }
     }

     for(int i = ; i <= n; i++) {
         my[stk[i].a[]] = str[stk[i].b[]];
     }
     printf("! ");
     for(int i = ; i <= n; i++) {
         putchar(my[i]);
     }
     puts("");
     return ;
 }

AC代码

这题还有一种CRT解法......

具体来说，对每个位置i，考虑它是从哪来的，设从pos来。

那么我们先询问三次，如下图。

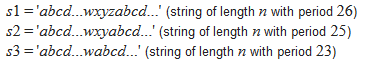
然后那么对于i来说，pos % 23 = s1[i] - 'a'。然后解方程即可。

CF1146G Zoning Restrictions

题意：你要在长为n的位置上填上[0, h]的数，如果填了x就会得到x²块钱。有m个限制，形如如果在[l, r]中有数超过了y，就要付c块钱。求最多钱数。n,m,h <= 50。

解：有一种网络流做法是最小割。

考虑切糕，把每个位置的取值都串起来，因为要最小，就先假设填了h，填x就是h² - x²。对于限制，额外连向一个新点，向t连边为c。

 #include <bits/stdc++.h>

 const int N = , INF = 0x3f3f3f3f;

 struct Edge {
     int nex, v, c;
     Edge(){}
     Edge(int N, int V, int C) {
         nex = N;
         v = V;
         c = C;
     }
 }edge[]; int tp = ;

 int e[N], n, h, m, vis[N], d[N];
 std::queue<int> Q;

 inline void add(int x, int y, int z) {
     edge[++tp] = Edge(e[x], y, z);
     e[x] = tp;
     edge[++tp] = Edge(e[y], x, );
     e[y] = tp;
     return;
 }

 inline bool BFS(int s, int t) {
     static int Time = ;
     Q.push(s);
     ++Time;
     vis[s] = Time;
     d[s] = ;
     while(Q.size()) {
         int x = Q.front();
         Q.pop();
         for(int i = e[x]; i; i = edge[i].nex) {
             int y = edge[i].v;
             if(vis[y] != Time && edge[i].c) {
                 vis[y] = Time;
                 d[y] = d[x] + ;
                 Q.push(y);
             }
         }
     }
     return vis[t] == Time;
 }

 int DFS(int x, int t, int maxF) {
     if(x == t) {
         return maxF;
     }
     int ans = ;
     for(int i = e[x]; i; i = edge[i].nex) {
         int y = edge[i].v;
         if(d[x] +  != d[y] || !edge[i].c) {
             continue;
         }
         int temp = DFS(y, t, std::min(maxF - ans, edge[i].c));
         if(!temp) {
             d[y] = INF;
         }
         ans += temp;
         edge[i].c -= temp;
         edge[i ^ ].c += temp;
         if(ans == maxF) {
             break;
         }
     }
     return ans;
 }

 inline int solve(int s, int t) {
     int ans = ;
     while(BFS(s, t)) {
         ans += DFS(s, t, INF);
     }
     return ans;
 }

 inline int id(int x, int y) {
     return (x - ) * (h + ) + y + ;
 }

 int main() {

     scanf("%d%d%d", &n, &h, &m);
     int s = (h + ) * n + m + , t = s + , lm = (h + ) * n, V = h * h;
     for(int i = ; i <= n; i++) {
         add(s, id(i, ), INF);
         add(id(i, h + ), t, INF);
         for(int j = ; j <= h; j++) {
             add(id(i, j), id(i, j + ), V - j * j);
         }
     }
     for(int i = ; i <= m; i++) {
         int l, r, x, y;
         scanf("%d%d%d%d", &l, &r, &x, &y);
         if(x == h) continue;
         int p = lm + i;
         add(p, t, y);
         for(int j = l; j <= r; j++) {
             add(id(j, x + ), p, INF);
         }
     }

     int ans = n * h * h;
     ans -= solve(s, t);
     printf("%d\n", ans);
     return ;
 }

AC代码

还有一种区间DP解法，我并不会...

CF1147D - Palindrome XOR

题意：求有多少对长度不超过n的无前导0的回文01串满足异或起来恰好为s。s的第一位一定是1，存在通配符。n <= 1000

解：这个1000很有趣....可以O(n)枚举第二个串的开头在哪。

然后发现这个回文和异或都是些形如“它们相等”或者“它们不等”的限制。于是考虑用并查集处理这些限制，每个连通块有两种取值。边带权并查集即可。

 #include <bits/stdc++.h>

 const int N = , MO = ;

 char str[N];
 int n;

 inline int qpow(int a, int b) {
     int ans = ;
     while(b) {
         if(b & ) ans = 1ll * ans * a % MO;
         a = 1ll * a * a % MO;
         b = b >> ;
     }
     return ans;
 }

 namespace ufs {
     int cnt, fa[N * ], val[N * ];
     inline void init() {
         for(int i = ; i <= n *  + ; i++) {
             fa[i] = i;
             val[i] = ;
         }
         cnt =  * n;
         return;
     }
     int find(int x, int &v) {
         if(x == fa[x]) {
             v = ;
             return x;
         }
         int t = find(fa[x], v);
         v ^= val[x];
         fa[x] = t;
         val[x] = v;
         return t;
     }
     inline bool merge(int x, int y, int v) {
         int t, t2;
         x = find(x, t);
         y = find(y, t2);
         t ^= t2;
         if(x == y) {
             if(t != v) return false;
             return true;
         }
         else {
             fa[x] = y;
             val[x] = v ^ t;
             cnt--;
         }
         return true;
     }
 }
 using ufs::merge;

 int main() {
     scanf("%s", str + );
     n = strlen(str + );
     std::reverse(str + , str + n + );
     int ans = , Z =  * n + ;
     for(int i = n - ; i >= ; i--) {
         ufs::init();
         if(!merge(n, Z, )) continue;
         if(!merge(, Z, )) continue;
         if(!merge(n + , Z, )) continue;
         if(!merge(n + i, Z, )) continue;
         int fd = ;
         for(int j = n; j > i; j--) {
             if(!merge(n + j, Z, )) {
                 fd = ; break;
             }
         }
         if(fd) continue;
         for(int j = ; j *  <= n; j++) {
             if(!merge(j, n - j + , )) {
                 fd = ;
                 break;
             }
         }
         if(fd) continue;
         for(int j = ; j *  <= i; j++) {
             if(!merge(n + j, n + i - j + , )) {
                 fd = ;
                 break;
             }
         }
         if(fd) continue;
         for(int j = ; j <= n; j++) {
             if(str[j] != '?') {
                 if(!merge(j, n + j, str[j] - '')) {
                     fd = ;
                     break;
                 }
             }
         }
         if(fd) continue;
         ans = (ans + qpow(, ufs::cnt)) % MO;
     }
     printf("%d\n", ans);
     return ;
 }

AC代码