【机器学习】--EM算法从初识到应用
一、前述
Em算法是解决数学公式的一个算法,是一种无监督的学习。
EM算法是一种解决存在隐含变量优化问题的有效方法。EM算法是期望极大(Expectation Maximization)算法的简称,EM算法是一种迭代型的算法,在每一次的迭代过程中,主要分为两步:即求期望(Expectation)步骤和最大化(Maximization)步骤。
二、具体
1、高斯混合模型
所谓混合高斯模型(GMM)就是指对样本的概率密度分布进行估计,而估计采用的模型(训练模型)是几个高斯模型的加权和(具体是几个要在模型训练前建立好)。每个高斯模型就代表了一个类(一个Cluster)。对样本中的数据分别在几个高斯模型上投影,就会分别得到在各个类上的概率。得出一个概率有很多好处,因为它的信息量比简单的一个结果要多,比如,我可以把这个概率转换为一个 score ,表示算法对自己得出的这个结果的把握。简单的说就是:m个样本{x1,...xm},可以分为k类,每个类别都服从高斯分布。

2、EM算法概述
EM算法实际上是一个不停迭代计算的过程,根据我们事先估计的先验概率A,得出一个结果B,再根据结果B,再计算得到结果A,然后反复。
可以想象饭店的后方大厨,炒了两盘一样的菜,现在,菜炒好后从锅中倒入盘,不可能一下子就分配均匀,所以先往两盘中倒入,然后发现B盘菜少了,就从A中匀出一些,A少了,从B匀.......不停迭代。
给定训练样本{x1,...xm}(与k-means中的样本一样是没有标签的,因此EM也是非监督学习方法),认为他们满足高斯分布 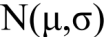 , 求估计参数
, 求估计参数 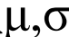 。
。
【机器学习】--EM算法从初识到应用的更多相关文章
- 机器学习-EM算法-pLSA模型笔记
pLSA模型--基于概率统计的pLSA模型(probabilistic Latent Semantic Analysis,概率隐语义分析),增加了主题模型,形成简单的贝叶斯网络,可以使用EM算法学习模 ...
- 机器学习-EM算法笔记
EM算法也称期望最大化(Expectation-Maximum,简称EM)算法,它是一个基础算法,是很多机器学习领域算法的基础,比如隐式马尔科夫算法(HMM), LDA主题模型的变分推断,混合高斯模型 ...
- 机器学习——EM算法
1 数学基础 在实际中,最小化的函数有几个极值,所以最优化算法得出的极值不确实是否为全局的极值,对于一些特殊的函数,凸函数与凹函数,任何局部极值也是全局极致,因此如果目标函数是凸的或凹的,那么优化算法 ...
- 机器学习-EM算法
最大期望算法 EM算法的正式提出来自美国数学家Arthur Dempster.Nan Laird和Donald Rubin,其在1977年发表的研究对先前出现的作为特例的EM算法进行了总结并给出了标准 ...
- 机器学习-EM算法的收敛证明
上一篇开头说过1983年,美国数学家吴建福(C.F. Jeff Wu)给出了EM算法在指数族分布以外的收敛性证明. EM算法的收敛性只要我们能够证明对数似然函数的值在迭代的过程中是增加的 即可: 证明 ...
- 机器学习——EM算法与GMM算法
目录 最大似然估计 K-means算法 EM算法 GMM算法(实际是高斯混合聚类) 中心思想:①极大似然估计 ②θ=f(θold) 此算法非常老,几乎不会问到,但思想很重要. EM的原理推导还是蛮复杂 ...
- 机器学习-EM算法-GMM模型笔记
GMM即高斯混合模型,下面根据EM模型从理论公式推导GMM: 随机变量X是有K个高斯分布混合而成,取各个高斯分布的概率为φ1,φ2,... ,φK,第i个高斯分布的均值为μi,方差为Σi.若观测到随机 ...
- opencv3中的机器学习算法之:EM算法
不同于其它的机器学习模型,EM算法是一种非监督的学习算法,它的输入数据事先不需要进行标注.相反,该算法从给定的样本集中,能计算出高斯混和参数的最大似然估计.也能得到每个样本对应的标注值,类似于kmea ...
- 简单易学的机器学习算法——EM算法
简单易学的机器学习算法——EM算法 一.机器学习中的参数估计问题 在前面的博文中,如“简单易学的机器学习算法——Logistic回归”中,采用了极大似然函数对其模型中的参数进行估计,简单来讲即对于一系 ...
随机推荐
- python3 os模块的常用功能及方法总结
1.os.getcwd() #显示当前工作路径 2.os.listdir('dirname') #返回指定目录下的所有文件和目录名 3.os.remove('filename') ...
- BITE
<Google软件测试之道> 读后感言: p147 提到的BITE实在是太让人心动了, 一个简单的动作即可提交一个信息齐全的bug,连非专业测试人员也能轻松做到.身边很多人也都碰到过提交b ...
- js生成带logo的二维码
作为一名java程序员,一直以来都是使用服务端生成二维码,最近接触前端的设计,感觉二维码这块如果放到前端去生成,一方面可以减轻服务端的压力,访问带宽,另一方面,前端页面控制比较顺畅 闲话少叙,说下我的 ...
- bzoj5252 [2018多省省队联测]林克卡特树
斜率优化树形dp?? 我们先将问题转化成在树上选K+1条互不相交路径,使其权值和最大. 然后我们考虑60分的dp,直接维护每个点子树内选了几条路径,然后该点和0/1/2条路径相连 然后我们会发现最后的 ...
- B20J_1419_Red Is Good_期望DP
B20J_1419_red is good_期望DP 题意:有R张红牌和B张黑牌,一张一张地翻牌,翻到红牌得到1美元,黑牌则付出1美元.可以随时停止翻牌,在最优策略下平均能得到多少钱. 分析:期望DP ...
- BZOJ_1778_[Usaco2010 Hol]Dotp 驱逐猪猡_概率DP+高斯消元
BZOJ_1778_[Usaco2010 Hol]Dotp 驱逐猪猡_概率DP+高斯消元 题意: 奶牛们建立了一个随机化的臭气炸弹来驱逐猪猡.猪猡的文明包含1到N (2 <= N <= 3 ...
- JAVA基础第三章-类与对象、抽象类、接口
业内经常说的一句话是不要重复造轮子,但是有时候,只有自己造一个轮子了,才会深刻明白什么样的轮子适合山路,什么样的轮子适合平地! 我将会持续更新java基础知识,欢迎关注. 往期章节: JAVA基础第一 ...
- 【RecyclerView优化】
1.局部刷新 (1)避免整个列表的数据更新,只更新受影响的布局.例如,加载更多时,不使用notifyDataSetChanged(),而是使用notifyItemRangeInserted(range ...
- 约定Service构建方式
对于DevOps中,将开发好的软件交付给运维人员去部署与维护,过程中参杂着诸多不可控制的变量,如环境问题.版本问题等等,而Docker容器极大程度上解决了这些问题,同时对于服务的持续交付,也变得方便和 ...
- CBC 字节反转攻击
一.CBC 简介 现代密码体制 现代密码中的加密体制一般分为对称加密体制(Symmetric Key Encryption)和非对称加密体制(Asymmetric Key Encryption).对称 ...
