poj 3321(树状数组)

Apple Tree

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 24954		Accepted: 7447

Description

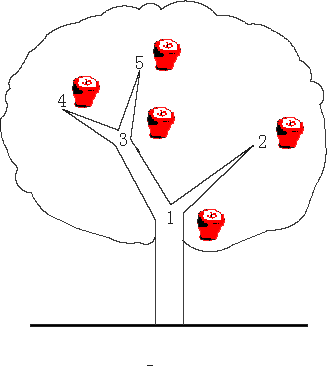
There is an apple tree outside of kaka's house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.

The tree has N forks which are connected by branches. Kaka numbers the forks by 1 to N and the root is always numbered by 1. Apples will grow on the forks and two apple won't grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.

The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?

Input

The first line contains an integer N (N ≤ 100,000) , which is the number of the forks in the tree.
The following N - 1 lines each contain two integers u and v, which means fork u and fork v are connected by a branch.
The next line contains an integer M (M ≤ 100,000).
The following M lines each contain a message which is either
"C x" which means the existence of the apple on fork x has been changed. i.e. if there is an apple on the fork, then Kaka pick it; otherwise a new apple has grown on the empty fork.
or
"Q x" which means an inquiry for the number of apples in the sub-tree above the fork x, including the apple (if exists) on the fork x
Note the tree is full of apples at the beginning

Output

For every inquiry, output the correspond answer per line.

Sample Input

3
1 2
1 3
3
Q 1
C 2
Q 1

Sample Output

3
2

题意:一棵树上有n个结点，每个节点上面都有一个苹果，现在给两个操作：
C x 如果第 x 个节点上存在苹果，则摘掉，如果没有，那么会长一个出来。
Q x 问 x 的子树里面有多少个苹果。
题解:DFS进行节点的重新标记，求出每个结点的"管辖范围"，然后每次更新左区间，求和就用sum(R[x]) - sum(L[x]-1)

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <stack>
#include <vector>
using namespace std;
const int N = ;
int L[N],R[N],c[N]; ///[L[i],R[i]] 是第i个点的管辖范围
bool flag[N];
int n,key;
vector <int> edge[N];
int lowbit(int x){
    return x&(-x);
}
void update(int idx,int v){
    for(int i=idx;i<=n;i+=lowbit(i)){
        c[i]+=v;
    }
}
int getsum(int idx){
    int sum = ;
    for(int i=idx;i>=;i-=lowbit(i)){
        sum+=c[i];
    }
    return sum;
}
void dfs(int idx){
    L[idx] = key;
    for(int i=;i<edge[idx].size();i++){
        key+=;
        dfs(edge[idx][i]);
    }
    R[idx] = key;
}
int main()
{
    while(scanf("%d",&n)!=EOF){
        key = ;
        memset(c,,sizeof(c));
        memset(flag,false,sizeof(flag));
        for(int i=;i<=n;i++) edge[i].clear();
        for(int i=;i<n;i++){
            int u,v;
            scanf("%d%d",&u,&v);
            edge[u].push_back(v);
        }
        dfs();
        for(int i=;i<=n;i++){
            update(i,);
        }
        int q;
        scanf("%d",&q);
        while(q--){
            char s[];
            int x;
            scanf("%s%d",s,&x);
            if(s[]=='Q'){
                printf("%d\n",getsum(R[x])-getsum(L[x]-));
            }else{
                if(flag[x]){
                    update(L[x],);
                }else update(L[x],-);
                flag[x] = !flag[x];
            }
        }
    }
    return ;
}