NOIP2014提高组 联合权值（距离为2的树形dp）

联合权值

题目描述

无向连通图 GG 有 nn 个点，n-1n−1 条边。点从 11 到 nn 依次编号,编号为 ii 的点的权值为 W_iWi​，每条边的长度均为 11。图上两点 (u, v)(u,v) 的距离定义为 uu 点到 vv 点的最短距离。对于图 GG 上的点对 (u, v)(u,v)，若它们的距离为 22，则它们之间会产生W_v \times W_uWv​×Wu​ 的联合权值。

请问图 GG 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入输出格式

输入格式：

第一行包含 11 个整数 nn。

接下来 n-1n−1 行,每行包含 22 个用空格隔开的正整数 u,vu,v，表示编号为 uu 和编号为 vv 的点之间有边相连。

最后 11 行,包含 nn 个正整数，每两个正整数之间用一个空格隔开，其中第 ii 个整数表示图 GG 上编号为 ii 的点的权值为 W_iWi​。

输出格式：

输出共 11 行,包含 22 个整数，之间用一个空格隔开,依次为图 GG 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对1000710007取余。

输入输出样例

输入样例#1： 复制

5
1 2
2 3
3 4
4 5
1 5 2 3 10 

输出样例#1： 复制

20 74

说明

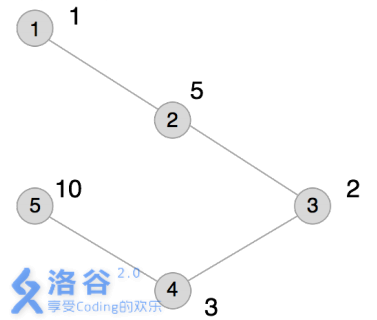
本例输入的图如上所示，距离为2 的有序点对有( 1,3)(1,3) 、( 2,4)(2,4) 、( 3,1)(3,1) 、( 3,5)(3,5)、( 4,2)(4,2) 、( 5,3)(5,3)。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30%的数据，1 < n \leq 1001<n≤100；

对于60%的数据，1 < n \leq 20001<n≤2000；

对于100%的数据，1 < n \leq 200000, 0 < W_i \leq 100001<n≤200000,0<Wi​≤10000。

保证一定存在可产生联合权值的有序点对。

在无边权的树上随意指定一个节点为根，那么我们会发现树上距离为2的节点只有两种情况：

1.两个节点为“祖父-孙子”

2.两个节点互为兄弟

“祖父-孙子”这种情况比较好解决，在dfs遍历树的时候不仅仅传递父亲(f)，还把祖父(g)一起传递

那么联合权值就为w[r]*w[g]（记录总和时要乘2）

那么我们看看兄弟情况该如何解决

设一个节点r的儿子分别是son[1],son[2],son[3]...

那么他们的最大值显然是son中最大值乘上次大值

总和也很好搞，记录一下son中w总和，平方一下，再减去son[i]与son[i]（自己配自己）这样不合法的情况即可

这些都是可以在dfs时顺道完成的

所以我们的时间复杂度就是O(n)

#include<bits/stdc++.h>
#define MAX 200005
#define MOD 10007
using namespace std;
typedef long long ll;

int n;
ll maxx,sum;
ll a[MAX],dpm[MAX],dps[MAX];
vector<int> v[MAX];
vector<ll> vv;

void dfs(int pre,int x){
    dpm[x]=;dps[x]=;
    for(int i=;i<v[x].size();i++){
        int to=v[x][i];
        if(to==pre) continue;
        dfs(x,to);
        dpm[x]=max(dpm[x],a[to]);
        maxx=max(maxx,a[x]*dpm[to]);
        dps[x]+=a[to];
        dps[x]%=MOD;
        sum+=a[x]*dps[to]*2ll;
        sum%=MOD;
    }
    vv.clear();
    for(int i=;i<v[x].size();i++){
        int to=v[x][i];
        if(to==pre) continue;
        vv.push_back(a[to]);
        sum+=a[to]*(dps[x]-a[to]+MOD);
        sum%=MOD;
    }
    if(vv.size()>){
        sort(vv.begin(),vv.end());
        maxx=max(maxx,vv[vv.size()-]*vv[vv.size()-]);
    }
}
int main()
{
    int t,i,j;
    int x,y;
    scanf("%d",&n);
    for(i=;i<n;i++){
        scanf("%d%d",&x,&y);
        v[x].push_back(y);
        v[y].push_back(x);
    }
    for(i=;i<=n;i++){
        scanf("%lld",&a[i]);
    }
    maxx=;sum=;
    dfs(-,);
    printf("%lld %lld\n",maxx,sum);
    return ;
}