Leetcode 587.安装栅栏

安装栅栏

在一个二维的花园中，有一些用 (x, y) 坐标表示的树。由于安装费用十分昂贵，你的任务是先用最短的绳子围起所有的树。只有当所有的树都被绳子包围时，花园才能围好栅栏。你需要找到正好位于栅栏边界上的树的坐标。

示例 1:

输入: [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]

输出: [[1,1],[2,0],[4,2],[3,3],[2,4]]

解释:

示例 2:

输入: [[1,2],[2,2],[4,2]]

输出: [[1,2],[2,2],[4,2]]

解释:

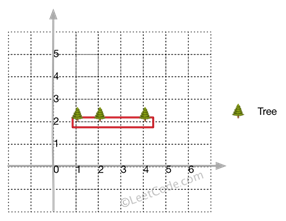
即使树都在一条直线上，你也需要先用绳子包围它们。

注意:

1. 所有的树应当被围在一起。你不能剪断绳子来包围树或者把树分成一组以上。
2. 输入的整数在 0 到 100 之间。
3. 花园至少有一棵树。
4. 所有树的坐标都是不同的。
5. 输入的点没有顺序。输出顺序也没有要求。

Graham扫描法

我给了它一个新名字，边界扫描法。用到的性质和解法二密切相关，首先也需要对某个维度进行从小达到排序。这样我们就能确定其中一个顶点了，我们选择横坐标最小的那个点作为整个坐标的原点。

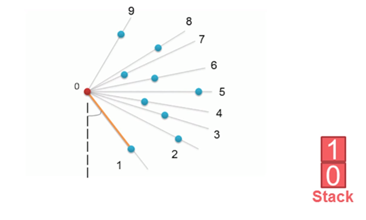
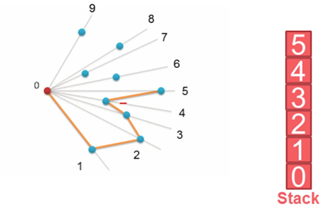
算法步骤：

1. 把所有点放在二维坐标系中，则纵坐标最小的点一定是凸包上的点，如图中的P0。

2. 把所有点的坐标平移一下，使 P0 作为原点，如上图。

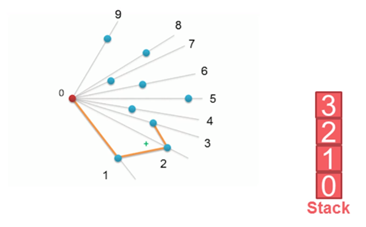
3. 计算各个点相对于 P0 的幅角 α ，按从小到大的顺序对各个点排序。当 α 相同时，距离 P0 比较近的排在前面。例如上图得到的结果为 P1，P2，P3，P4，P5，P6，P7，P8。我们由几何知识可以知道，结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。

（以上是准备步骤，以下开始求凸包）

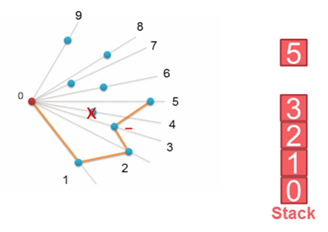
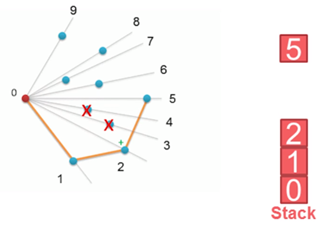
以上，我们已经知道了凸包上的第一个点 P0 和第二个点 P1，我们把它们放在栈里面。现在从步骤3求得的那个结果里，把 P1 后面的那个点拿出来做当前点，即 P2 。接下来开始找第三个点：

4. 连接P0和栈顶的那个点，得到直线 L 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5；如果在直线上，或者在直线的左边就执行步骤6。

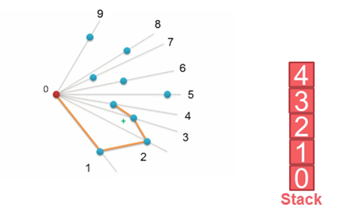
5. 如果在右边，则栈顶的那个元素不是凸包上的点，把栈顶元素出栈。执行步骤4。

6. 当前点是凸包上的点，把它压入栈，执行步骤7。

7. 检查当前的点 P2 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点，返回步骤4。

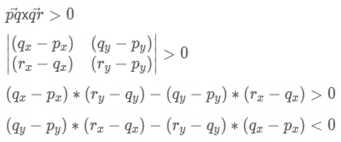
 public class Solution {
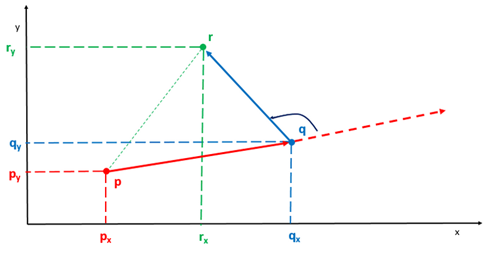
     public int orientation(Point p, Point q, Point r) {
         return (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y);
     }
     public int distance(Point p, Point q) {
         return (p.x - q.x) * (p.x - q.x) + (p.y - q.y) * (p.y - q.y);
     }
     private static Point bottomLeft(Point[] points) {
         Point bottomLeft = points[0];
         for (Point p: points)
             if (p.y < bottomLeft.y)
                 bottomLeft = p;
         return bottomLeft;
     }
     public List <Point> outerTrees(Point[] points) {
         if (points.length <= 1)
             return Arrays.asList(points);
         Point bm = bottomLeft(points);
         Arrays.sort(points, new Comparator< Point >() {
             public int compare(Point p, Point q) {
                 double diff = orientation(bm, p, q) - orientation(bm, q, p);
                 if (diff == 0)
                     return distance(bm, p) - distance(bm, q);
                 else
                     return diff > 0 ? 1 : -1;
             }
         });
         int i = points.length - 1;
         while (i >= 0 && orientation(bm, points[points.length - 1], points[i]) == 0)
             i--;
         for (int l = i + 1, h = points.length - 1; l < h; l++, h--) {
             Point temp = points[l];
             points[l] = points[h];
             points[h] = temp;
         }
         Stack < Point > stack = new Stack< >();
         stack.push(points[0]);
         stack.push(points[1]);
         for (int j = 2; j < points.length; j++) {
             Point top = stack.pop();
             while (orientation(stack.peek(), top, points[j]) > 0)
                 top = stack.pop();
             stack.push(top);
             stack.push(points[j]);
         }
         return new ArrayList<>(stack);
     }
 }