Git回版本回退

这里我们使用命令行的方式对已经提交的版本进行强行回退操作~~~

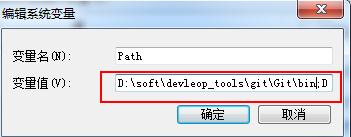
一、将git的安装目录bin放到path路径中,

如下图所示：

二、进入cmd界面，依次输入下面内容即可（git 远程仓库 回退到指定版本）

git checkout branches        　　#检出当前分支 
git branch branches_bak   　　#备份相关分支
git reset --hard 版本号        　　#将本地代码强行回退到指定的版本号
git push -f origin branches       #将本地分支强行push到远程分支上面

下面是我的相关执行操作，仅供参考：

Microsoft Windows [版本 6.1.7601]
版权所有 (c) 2009 Microsoft Corporation。保留所有权利。
D:\soft\devleop_tools\ideaUI\IntelliJ IDEA 14.1.3\workspace\fclient-git>git checkout branches
Already on 'branches'
Your branch is up-to-date with 'origin/branches'.

D:\soft\devleop_tools\ideaUI\IntelliJ IDEA 14.1.3\workspace\fclient-git>git branch branches_bak
D:\soft\devleop_tools\ideaUI\IntelliJ IDEA 14.1.3\workspace\fclient-git>git reset --hard cfdbafc7
HEAD is now at cfdbafc 修改登录相关的配置                                                                                                                                                                 

Warning: Your console font probably doesn't support Unicode. If you experience strange characters in the output, consider switching to a TrueType font such as Consolas!

D:\soft\devleop_tools\ideaUI\IntelliJ IDEA 14.1.3\workspace\fclient-git>git reset --hard cfdbafc7
HEAD is now at cfdbafc 修改登录相关的配置                                                                                                                                                                 

Warning: Your console font probably doesn't support Unicode. If you experience strange characters in the output, consider switching to a TrueType font such as Consolas!

D:\soft\devleop_tools\ideaUI\IntelliJ IDEA 14.1.3\workspace\fclient-git>git push -f origin braches
error: src refspec braches does not match any.
error: failed to push some refs to 'http://***.com/app/**.git'

D:\soft\devleop_tools\ideaUI\IntelliJ IDEA 14.1.3\workspace\fclient-git>git push -f origin branches
Username for 'http://***.com': zhanghao80
Password for 'http://zhanghao80@***.com':
Total 0 (delta 0), reused 0 (delta 0)
remote: Updating references: 100% (1/1)
To http://***.com/app/**.git
 + bfdb901...cfdbafc branches -> branches (forced update)

D:\soft\devleop_tools\ideaUI\IntelliJ IDEA 14.1.3\workspace\fclient-git>

　　

　　

Thank is all ~~