c++ 搜索二叉树 插入，删除，遍历操作
搜索二叉树是一种具有良好排序和查找性能的二叉树数据结构，包括多种操作，本篇只介绍插入，排序（遍历），和删除操作，重点是删除操作比较复杂，用到的例子也是本人亲自画的
用到的测试图数据例子
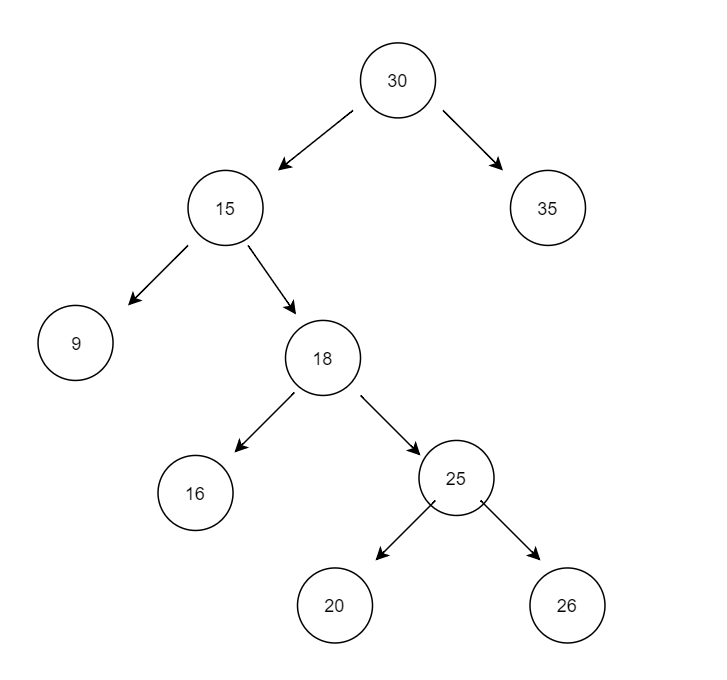
第一、构建节点
template <typename T> class BST;
template <typename T> class BSTNode {
public:
friend class BST<T>;
BSTNode() {
lChild = rChild = parent = NULL;
data = NULL;
}
BSTNode(T d) {
lChild = rChild = parent = NULL;
data = d;
}
private:
BSTNode<T> *lChild, *rChild, *parent;
T data;
};
第二、二叉树头文件定义
template<typename T> class BST {
public:
BST() { }
//插入操作
void insert(BSTNode<T>*node);
//二叉查找树的中序遍历，就相当于排序了
void inSort(BSTNode<T>*node);
//按节点删除
void deleteNode(BSTNode<T>* node);
//按数值删除
void deleteNode(const T& t);
BSTNode<T>* search(T key);
BSTNode<T>* root=NULL;
private:
int count;
};
第三、搜索二叉树的插入
1）如果二叉树查找树为空节点，则插入节点就为根节点
2）如果二叉查找树为非空节点，就需要先找到待插入节点，查找原则就是从根节点开始，如果大于根就右边走，小于根就左边走，直到找到合适节点，
下面代码中的最终找到的temp 就是待插入节点.
template<typename T>
void BST<T>::insert(BSTNode<T>* node)
{
BSTNode<T>* curr, *temp = NULL;
curr = root;
while (NULL!= curr) //遍历二叉树，找到应该插入的父节点
{
temp = curr;
if (node->data>curr->data)
{
curr = curr->rChild;
}
else {
curr = curr->lChild;
}
}
node->parent = temp;//temp 代码当前最后遍历的node，设置node->parent为该节点
if (temp==NULL)
{
root = node;
count++;
}
else {
if (node->data<temp->data)
{
temp->lChild = node;
count++;
}
else {
temp->rChild = node;
count++;
}
}
}
第四、搜索二叉树的删除
删除包含多种情况，
1. 如果节点没有子女，修改其父节点指针为NULL，删除即可
2. 如果该节点有左孩子情况，修改其父亲节点的指针和其左孩子的parent指针即可
3. 如果该节点有右孩子情况，修改其父亲节点的指针和其右孩子的parent指针即可
4.如果同时有左右孩子的情况，情况比较复杂，一般有2种方法处理
1） 用节点右边孩子的最小值替换该节点，其他节点位置保持不变（本篇用这种方法）
2）用节点左边孩子的最大值替换该节点，其他节点位置保持不变
后面测试例子是删除18 node，通过程序找到右边最小值20，用20 替换18，其他节点位置保持不动。
template<typename T>
inline void BST<T>::deleteNode(BSTNode<T>* node)
{
BSTNode<T>*p = node->parent;//获取node的父节点，这里很重要
if (node->lChild==NULL && node->rChild==NULL) //叶子节点直接删除
{
if (node==node->parent->lChild)
{
node->parent->lChild = NULL;
}
else {
node->parent->rChild = NULL;
}
delete node;
count--;
}
else if (node->rChild != NULL && node->lChild == NULL) {//存在右孩子
if (p==NULL)//说明节点为根节点
{
root = node->rChild;
count--;
}
else {
node->rChild->parent = p;
if (p->lChild==node) //判断是父节点的左孩子还是右孩子
{
p->lChild = node->rChild;
}
else {
p->rChild = node->rChild;
}
delete node;
count--;
}
}
else if (node->lChild!=NULL && node->rChild==NULL)//存在左孩子
{
if (p==NULL)
{
root = root->lChild;
count--;
}
else {
node->lChild->parent = p;
if (p->lChild==node)
{
p->lChild = node->lChild;
}
else {
p->rChild = node->lChild;
}
delete node;
count--;
}
}
else {
BSTNode<T>*left, *curp=NULL;
left = node->rChild; //本方案是找右侧最小值，替换node节点，其他节点保持不动即可
while (left!=NULL)
{
curp = left;
left = left->lChild;
} if (curp->rChild!=NULL)
{
if (curp->lChild==curp)
{
curp->parent->lChild = curp->rChild;
}
else {
curp->parent->rChild = curp->rChild;
}
}
else {
if (curp->parent->lChild==curp)
{
curp->parent->lChild = NULL;
}
else {
curp->parent->rChild = NULL;
}
//curp->parent->lChild = NULL;
}
//替curp 替换 node
curp->parent = p;
curp->lChild = node->lChild;
curp->rChild = node->rChild; if (p->lChild==node)//判断node 是p 的左孩子还是右孩
{
p->lChild = curp;
}
else {
p->rChild = curp;
}
delete node;
count--;
}
}
第五、二叉树的搜索查找
由于搜索二叉树本身是已经排序好的，查找过程相对简单，从根节点，逐个排查，大于根向右，小于根向左，直到叶子节点.
template<typename T>
inline BSTNode<T>* BST<T>::search(T k)
{
BSTNode<T>*node = root;
while (node!=NULL)
{
if (k<node->data)
{
node = node->lChild;
}
else if (k> node->data)
{
node = node->rChild;
}
else {
break;
}
}
return node;
}
第六、二叉搜索树的排序
根据二叉所有树的特性，这里所谓排序，其实就是二叉树的中序遍历，其他的几种遍历不在这里赘述，知识调整下结构即可
template<typename T>
void BST<T>::inSort(BSTNode<T>* node)
{
if (node!=NULL)
{
inSort(node->lChild);
std::cout << node->data<<",";
inSort(node->rChild);
}
}
第七、测试程序
#include "pch.h"
#include <iostream>
#include "BSTree.h"
using namespace std; int main()
{
// 树结构示意
// 30
// / \
// 15 25
// / \
//9 18
// / \
// 16 25
// / \
// 20 26
BST<int> sbt;
sbt.insert(new BSTNode<int>());
sbt.insert(new BSTNode<int>());
sbt.insert(new BSTNode<int>());
sbt.insert(new BSTNode<int>());
sbt.insert(new BSTNode<int>());
sbt.insert(new BSTNode<int>());
sbt.insert(new BSTNode<int>());
sbt.insert(new BSTNode<int>());
sbt.insert(new BSTNode<int>()); cout << "搜索树排序后:";
sbt.inSort(sbt.root); sbt.deleteNode(); cout << endl << "删除18 后排序:"; sbt.inSort(sbt.root);
}
测试结果
所有完整程序代码
#pragma once
template <typename T> class BST;
template <typename T> class BSTNode {
public:
friend class BST<T>;
BSTNode() {
lChild = rChild = parent = NULL;
data = NULL;
}
BSTNode(T d) {
lChild = rChild = parent = NULL;
data = d;
}
private:
BSTNode<T> *lChild, *rChild, *parent;
T data;
}; template<typename T> class BST {
public:
BST() { } //插入操作
void insert(BSTNode<T>*node); //二叉查找树的中序遍历，就相当于排序了
void inSort(BSTNode<T>*node); //按节点删除
void deleteNode(BSTNode<T>* node); //按数值删除
void deleteNode(const T& t); BSTNode<T>* search(T key);
BSTNode<T>* root=NULL; private:
int count;
}; template<typename T>
void BST<T>::insert(BSTNode<T>* node)
{
BSTNode<T>* curr, *temp = NULL;
curr = root;
while (NULL!= curr) //遍历二叉树，找到应该插入的父节点
{
temp = curr;
if (node->data>curr->data)
{
curr = curr->rChild;
}
else {
curr = curr->lChild;
}
}
node->parent = temp;//temp 代码当前最后遍历的node，设置node->parent为该节点
if (temp==NULL)
{
root = node;
count++;
}
else {
if (node->data<temp->data)
{
temp->lChild = node;
count++;
}
else {
temp->rChild = node;
count++;
}
}
} template<typename T>
void BST<T>::inSort(BSTNode<T>* node)
{
if (node!=NULL)
{
inSort(node->lChild);
std::cout << node->data<<",";
inSort(node->rChild);
}
} template<typename T>
inline void BST<T>::deleteNode(BSTNode<T>* node)
{
BSTNode<T>*p = node->parent;//获取node的父节点，这里很重要
if (node->lChild==NULL && node->rChild==NULL) //叶子节点直接删除
{
if (node==node->parent->lChild)
{
node->parent->lChild = NULL;
}
else {
node->parent->rChild = NULL;
}
delete node;
count--;
}
else if (node->rChild != NULL && node->lChild == NULL) {//存在右孩子
if (p==NULL)//说明节点为根节点
{
root = node->rChild;
count--;
}
else {
node->rChild->parent = p;
if (p->lChild==node) //判断是父节点的左孩子还是右孩子
{
p->lChild = node->rChild;
}
else {
p->rChild = node->rChild;
}
delete node;
count--;
}
}
else if (node->lChild!=NULL && node->rChild==NULL)//存在左孩子
{
if (p==NULL)
{
root = root->lChild;
count--;
}
else {
node->lChild->parent = p;
if (p->lChild==node)
{
p->lChild = node->lChild;
}
else {
p->rChild = node->lChild;
}
delete node;
count--;
}
}
else {
BSTNode<T>*left, *curp=NULL;
left = node->rChild; //本方案是找右侧最小值，替换node节点，其他节点保持不动即可
while (left!=NULL)
{
curp = left;
left = left->lChild;
} if (curp->rChild!=NULL)
{
if (curp->lChild==curp)
{
curp->parent->lChild = curp->rChild;
}
else {
curp->parent->rChild = curp->rChild;
}
}
else {
if (curp->parent->lChild==curp)
{
curp->parent->lChild = NULL;
}
else {
curp->parent->rChild = NULL;
}
//curp->parent->lChild = NULL;
}
//替curp 替换 node
curp->parent = p;
curp->lChild = node->lChild;
curp->rChild = node->rChild; if (p->lChild==node)//判断node 是p 的左孩子还是右孩
{
p->lChild = curp;
}
else {
p->rChild = curp;
}
delete node;
count--;
}
} template<typename T>
inline void BST<T>::deleteNode(const T & k)
{
BSTNode<T>*node = search(k);
if (node!=NULL)
{
deleteNode(node);
}
} template<typename T>
inline BSTNode<T>* BST<T>::search(T k)
{
BSTNode<T>*node = root;
while (node!=NULL)
{
if (k<node->data)
{
node = node->lChild;
}
else if (k> node->data)
{
node = node->rChild;
}
else {
break;
}
}
return node;
}
BSTree.h
c++ 搜索二叉树 插入，删除，遍历操作的更多相关文章
- 【数据结构】——搜索二叉树的插入，查找和删除（递归&非递归）
一.搜索二叉树的插入,查找,删除 简单说说搜索二叉树概念: 二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值 若它的右 ...
- C 线性表的链式存储实现及插入、删除等操作示例
一.链式存储的优势 线性表的存储可以通过顺序存储或链式存储实现,其中顺序存储基于数组实现(见本人上一篇博客),在进行插入删除等操作时,需对表内某一部分元素逐个移动,效率较低.而链式结构不依赖于地址连续 ...
- [LeetCode] Insert Delete GetRandom O(1) - Duplicates allowed 常数时间内插入删除和获得随机数 - 允许重复
Design a data structure that supports all following operations in average O(1) time. Note: Duplicate ...
- [LeetCode] 381. Insert Delete GetRandom O(1) - Duplicates allowed 常数时间内插入删除和获得随机数 - 允许重复
Design a data structure that supports all following operations in average O(1) time. Note: Duplicate ...
- Java创建二叉搜索树，实现搜索，插入，删除操作
Java实现的二叉搜索树,并实现对该树的搜索,插入,删除操作(合并删除,复制删除) 首先我们要有一个编码的思路,大致如下: 1.查找:根据二叉搜索树的数据特点,我们可以根据节点的值得比较来实现查找,查 ...
- 数据结构--Avl树的创建，插入的递归版本和非递归版本，删除等操作
AVL树本质上还是一棵二叉搜索树,它的特点是: 1.本身首先是一棵二叉搜索树. 2.带有平衡条件:每个结点的左右子树的高度之差的绝对值最多为1(空树的高度为-1). 也就是说,AVL树,本质上 ...
- Java实现二叉树的创建和遍历操作（有更新）
博主强烈建议跳过分割线前面的部分,直接看下文更新的那些即可. 最近在学习二叉树的相关知识,一开始真的是毫无头绪.本来学的是C++二叉树,但苦于编译器老是出故障,于是就转用Java来实现二叉树的操作.但 ...
- jQuery---jq操作标签文本(html(),text()),jq操作文档标签(插入,删除,修改),克隆,,jq操作属性,jq操作class属性,jq操作表单value,jq操作css,jq操作盒子(重要),jq操作滚动条
jQuery---jq操作标签文本(html(),text()),jq操作文档标签(插入,删除,修改),克隆,,jq操作属性,jq操作class属性,jq操作表单value,jq操作css,jq操作盒 ...
- c++排序二叉树的出现的私有函数讨论，以及二叉树的删除操作详解
c++排序二叉树的出现的私有函数讨论, 以及二叉树的删除操作详解 标签(空格分隔): c++ 前言 我在c++学习的过程中, 最近打了一个排序二叉树的题目,题目中出现了私有函数成员,当时没有理解清楚这 ...
随机推荐
- Android.mk编译的写法
更多Android.mk的 用法见 :http://blog.csdn.net/fengbingchun/article/details/38705519 如何修改Android.mk 为Androi ...
- Selenium实现右键保存图片（Java）
1.代码 public class SaveImage extends TestCase { private WebDriver driver; private Actions action; pri ...
- 图像和流媒体 -- Sapera 安装遇到的问题
一.下载安装包 参看:Genie Nano M1930-NIR 点击软件及例程下载 二.安装遇到的问题 (1)Installation directory must be on a local har ...
- EasyPlayer RTSP Windows（with ActiveX/OCX插件）播放器支持H.265播放与抓图功能
EasyPlayer作为业界一款比较优秀的RTSP播放器,一直深受用户的好评,经过了近3年的开发和迭代,从一开始的简单PC版本的RTSP播放功能,到如今支持PC(支持ocx插件).Android.iO ...
- [置顶]
Android 关于SP读取与存储正确打开方式?
一.存储方式分类:SharedPreferences存储 二.SharedPreferences存储 1.特点 ①存储单一数据,例如数值,字符串,布尔 ②文件:/date/date/包名/shared ...
- Mac设置SVN：Cornerstone3
前因 在windows下用Tortoisesvn.可惜Tortoisesvn没有Mac版,只能上知乎寻找适合于 Mac的SVN软件. 经过 找到了一款名为Cornerstone的软件.在App Sto ...
- Delphi格式化函数Format、FormatDateTime和FormatFloat详解
转自:http://outofmemory.cn/code-snippet/7631/Delphi-format-hua-function-Format-FormatDateTime-FormatFl ...
- selenium-java,UI自动化截图方法
截图方法: import java.io.File; import java.io.IOException; import org.apache.commons.io.FileUtils; impor ...
- 浅析Java虚拟机结构与机制
转载自:http://blog.hesey.net/2011/04/introduction-to-java-virtual-machine.html http://coolshell.cn/arti ...
- BZOJ4602 Sdoi2016 齿轮 【带权并查集】*
BZOJ4602 Sdoi2016 齿轮 Description 现有一个传动系统,包含了N个组合齿轮和M个链条.每一个链条连接了两个组合齿轮u和v,并提供了一个传动比x : y.即如果只考虑这两个组 ...